17.09 Биссектриса и её свойства
Ошибка.
Попробуйте повторить позже
Докажите, что биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам.
Способ 1
Проведем через точку прямую
Тогда
как накрест лежащие, образованные параллельными прямыми
и
и секущей
Также
как соответственные, образованные параллельными прямыми
и
и секущей
— биссектриса, значит,
Таким образом, — равнобедренный, то есть
По теореме о пропорциональных отрезках
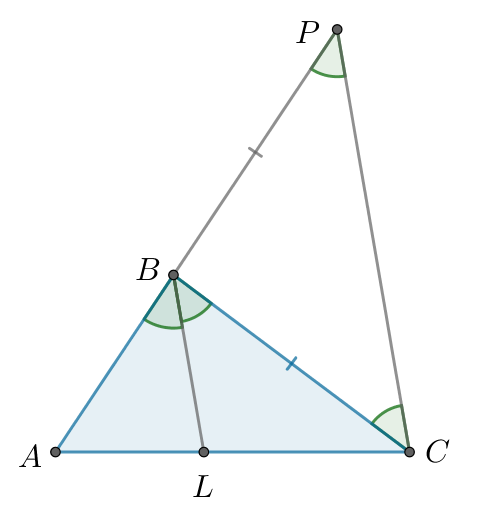
Способ 2
Рассмотрим треугольник и его биссектрису
. Не умаляя общности пусть в нем
. Если же
, то
биссектриса
, проведенная к основанию равнобедренного треугольника
, делит его пополам. Тогда
.
Итак, . Опустим из точек
и
перпендикуляры
и
на луч
. Определим, где будут лежать точки
и
.
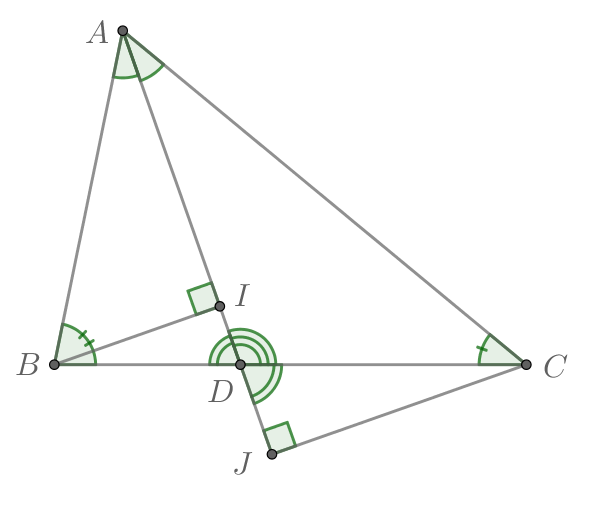
В треугольнике напротив большей стороны лежит больший угол, значит,
. Биссектриса
делит угол
пополам, то есть
. Угол
является внешним для треугольника
, следовательно,
.
Аналогично
. Тогда
. С другой стороны, эти углы являются смежными, то есть их сумма равна
, значит,
и
.
Вернемся к расположению точек и
. В треугольнике
углы
и
— острые, значит, основание перпендикуляра из
точки
на луч
будет лежать на отрезке
.
В треугольнике угол
— тупой, значит, основание перпендикуляра из точки
на луч
будет лежать на продолжении
за точку
.
Рассмотрим треугольники и
. Они подобны по двум углам, так как
и
. Тогда
выполняется следующее:
Рассмотрим треугольники и
. Они подобны по двум углам, так как
и
как
вертикальные. Тогда выполняется следующее:
Значит, биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам.
Ошибка.
Попробуйте повторить позже
Биссектриса внешнего угла треугольника
пересекает продолжение стороны
в точке
Докажите, что
Способ 1
Заметим, что если в треугольнике то биссектриса внешнего угла не будет пересекать основание
Тогда не
умаляя общности
Таким образом, биссектриса внешнего угла
будет пересекать продолжение стороны
за
точку
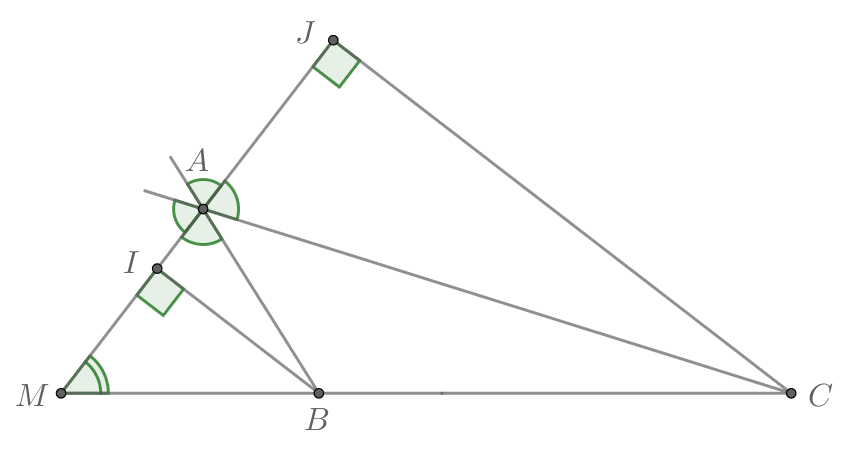
Опустим на внешнюю биссектрису угла из точек
и
перпендикуляры
и
Рассмотрим треугольники
и
В них
как половины внешнего угла
и
Значит, треугольники
и
подобны по двум углам, то есть
Рассмотрим треугольники и
Они подобны по двум углам, так как
и
— общий. Тогда выполняется следующее:
Способ 2
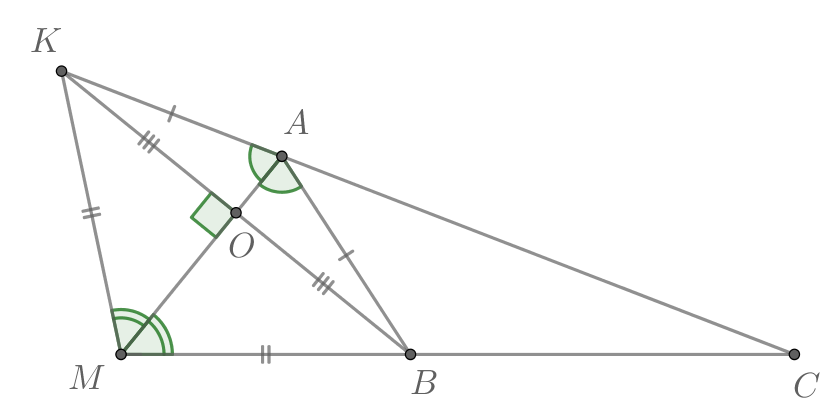
Отложим на прямой за точку
отрезок
Пусть
Тогда треугольник
—
равнобедренный. Так как
— биссектриса
то в треугольнике
— биссектриса. По свойству
равнобедренного треугольника
— высота и медиана. Тогда в треугольнике
— медиана и высота. Значит,
треугольник
— равнобедренный и
По свойству равнобедренного треугольника
— биссектриса
Тогда в треугольнике по свойству биссектрисы
Так как
то получаем нужное равенство:
Ошибка.
Попробуйте повторить позже
Найдите геометрическое место точек, равноудалённых от двух пересекающихся прямых.
Две пересекающиеся прямые разбивают плоскость на четыре части. Если точка лежит на биссектрисе одного из четырёх полученных углов, то она равноудалена от данных прямых. Обратно, произвольная точка плоскости, не лежащая ни на одной из данных прямых, расположена внутри одного из углов. Если она равноудалена от данных прямых, то она лежит на биссектрисе этого угла. Очевидно, что точка пересечения данных прямых также удовлетворяет условию задачи.
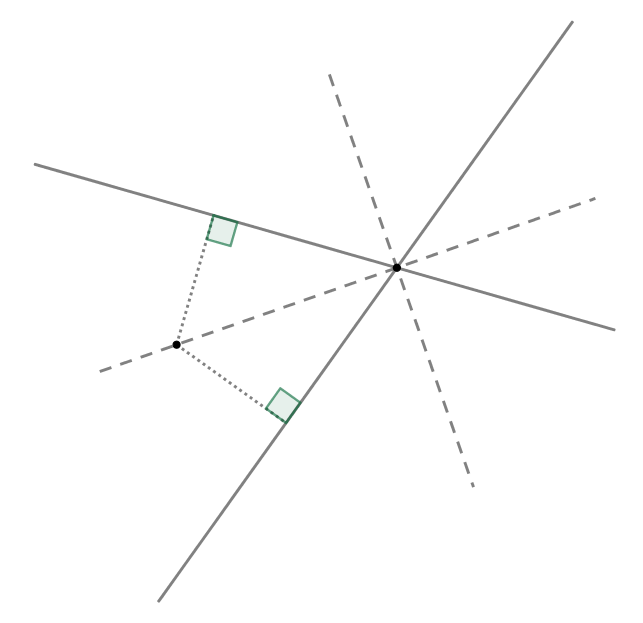
Биссектрисы углов, образованных при пересечении прямых.
Ошибка.
Попробуйте повторить позже
Докажите, что биссектрисы двух внешних углов и третьего внутреннего угла треугольника пересекаются в одной точке.
Рассмотрим точку пересечения биссектрис внешних углов
и
при вершинах
и
треугольника
. Поскольку точка
лежит на
биссектрисе угла
, то она равноудалена от прямых
и
;
поскольку точка
лежит на биссектрисе угла
, она равноудалена
от прямых
и
. Поэтому точка
равноудалена от сторон
угла
. Следовательно, она лежит на биссектрисе угла
.
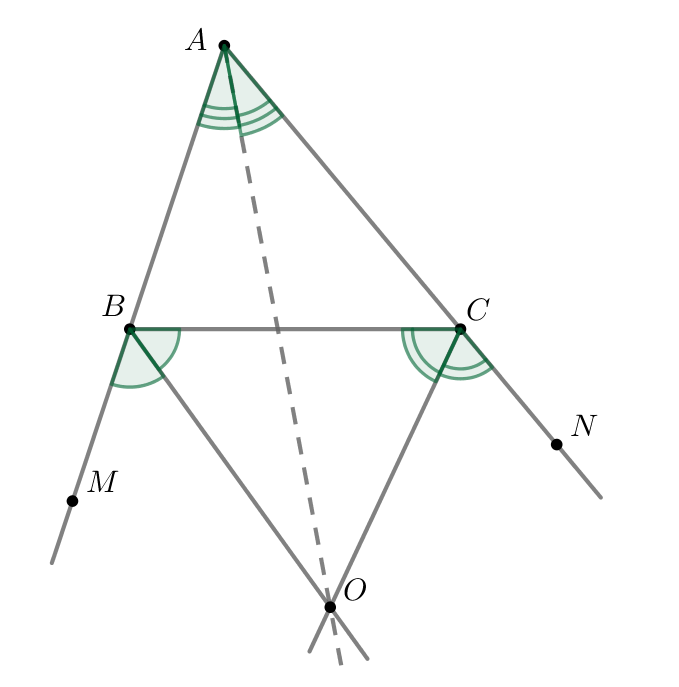
Что и требовалось доказать
Ошибка.
Попробуйте повторить позже
Биссектрисы трех углов четырехугольника пересекаются в одной точке. Длины трех его сторон в указанном порядке равны 3, 4, 6. Найдите четвертую сторону.
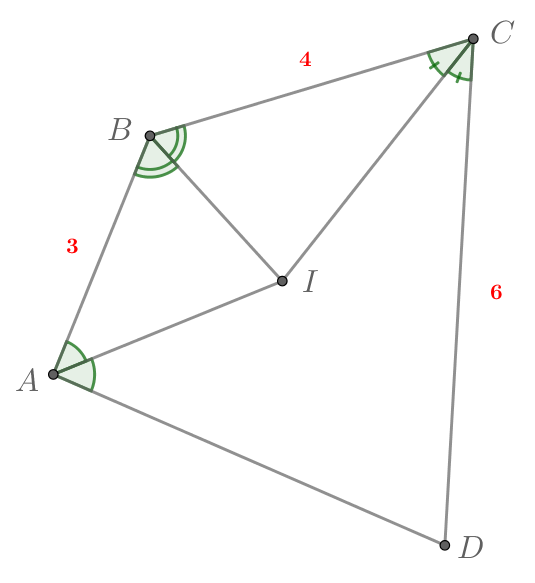
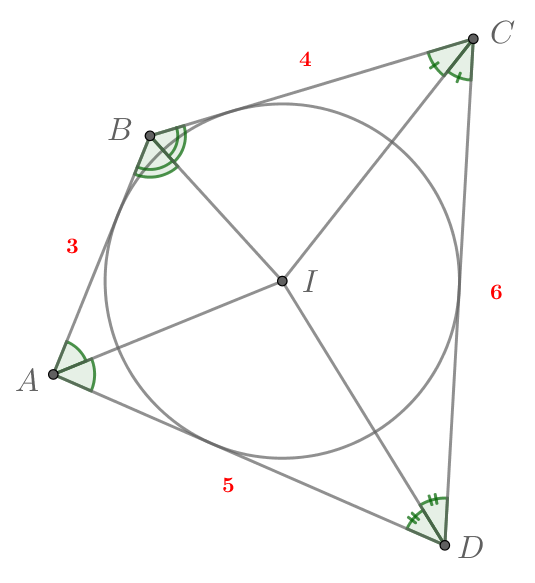
Пусть биссектрисы углов ,
и
пересекаются в точке
. Тогда
— биссектриса угла
, так как точка
равноудалена от всех
сторон четырехугольника. Значит,
— центр вписанной окружности четырехугольника
, то есть
— описанный. По
свойству описанного четырехугольника
, следовательно,
Ошибка.
Попробуйте повторить позже
В четырехугольнике внешний угол при вершине
равен углу
,
. Докажите, что
— биссектриса
угла
.
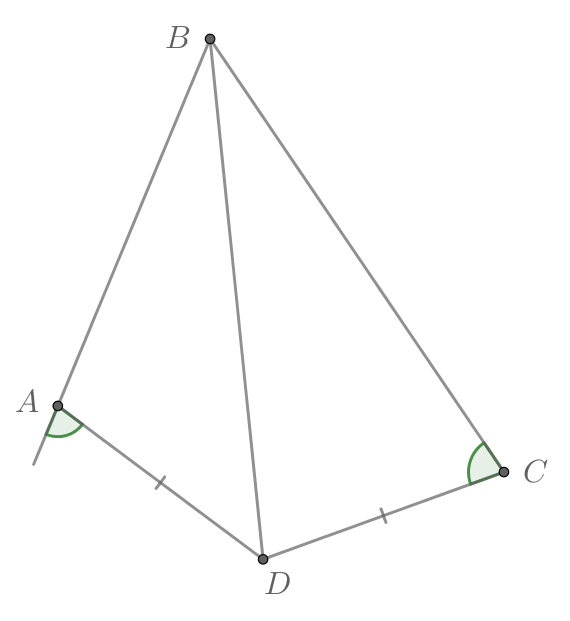
Пусть, не умаляя общности, . Если
, то
. В этом случае
точки
и
можно поменять местами, и задача не изменится. Случай, когда
, рассмотрим
позже.
Опустим из точки перпендикуляры
и
на прямые
и
соответственно. Тогда, так как
,
точка
упадет на продолжение прямой
за точку
, а точка
— на отрезок
.
Рассмотрим прямоугольные треугольники и
. Они равны по острому углу и гипотенузе (
и
). В равных треугольниках соответственные элементы равны, значит,
.
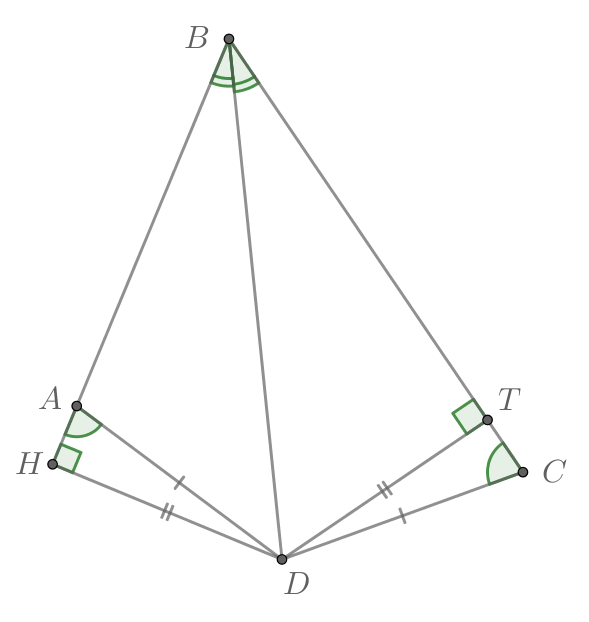
Таким образом, точка равноудалена от прямых
и
, следовательно,
— биссектриса угла
.
Если , то мы сразу можем получить, что точка
равноудалена от прямых
и
. Тогда она должна
лежать на биссектрисе угла
.
Задача на доказательство
Ошибка.
Попробуйте повторить позже
Через центр вписанной окружности треугольника провели прямую, параллельную одной из его сторон. Докажите, что эта прямая отсекает от данного треугольника меньший треугольник, периметр которого равен сумме двух сторон исходного треугольника.
![]()
Через центр вписанной окружности треугольника
провели прямую, параллельную стороне
Пусть она пересекает
стороны
и
треугольника
в точках
и
соответственно.
![]()
Центр вписанной окружности треугольника является точкой пересечения его биссектрис, значит, — биссектриса угла
Следовательно,
По условию значит,
как накрест лежащие. Тогда
Рассмотрим треугольник В нем
следовательно, треугольник
— равнобедренный, то есть
Аналогично — биссектриса угла
тогда треугольник
тоже равнобедренный и
Таким образом, периметр треугольника равен
Доказательство
Ошибка.
Попробуйте повторить позже
Провели биссектрисы двух внешних углов треугольника. Из точки их пересечения на его сторону опустили перпендикуляр. Он делит ее на отрезки с длинами 3 и 5. Найдите разность двух других сторон треугольника.
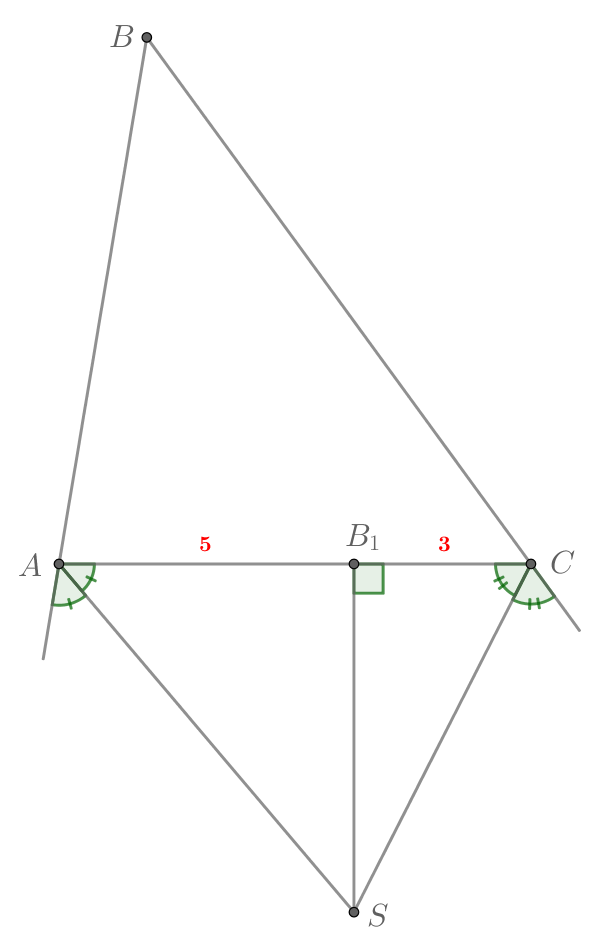
Пусть проведены биссектрисы внешних углов и
треугольника
, а
— их точка пересечения. Рассмотрим вневписанную
окружность с центром в точке
. Пусть она касается стороны
в точке
, а продолжений сторон
и
в точках
и
соответственно. Не умаляя общности, пусть
и
.
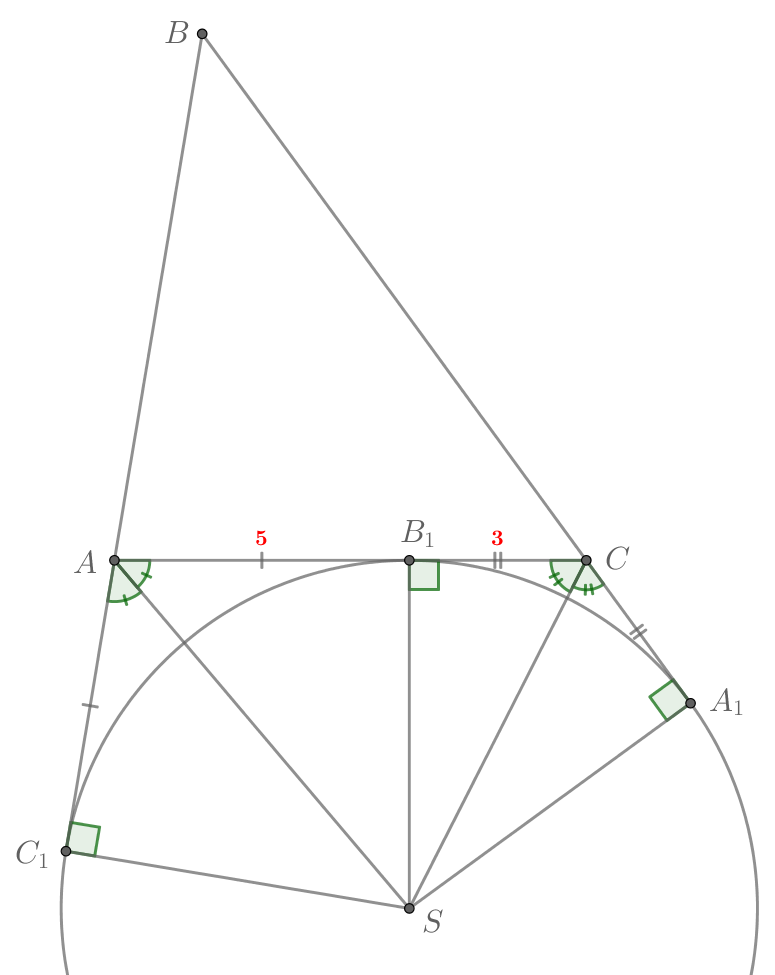
Отрезки касательных к окружности, проведенных из одной точки, равны, значит, ,
и
. Заметим,
что
и
, тогда
Задача на доказательство
Ошибка.
Попробуйте повторить позже
Биссектрисы соседних углов четырехугольника пересекаются в середине его стороны. Докажите, что либо у этого четырехугольника равны два угла, либо две стороны параллельны.
Рассмотрим рисунок. Если то доказывать нечего. Если нет, то
продолжим эти стороны до пересечения в точке
- 1.
- Пусть
лежит на продолжении стороны
за точку
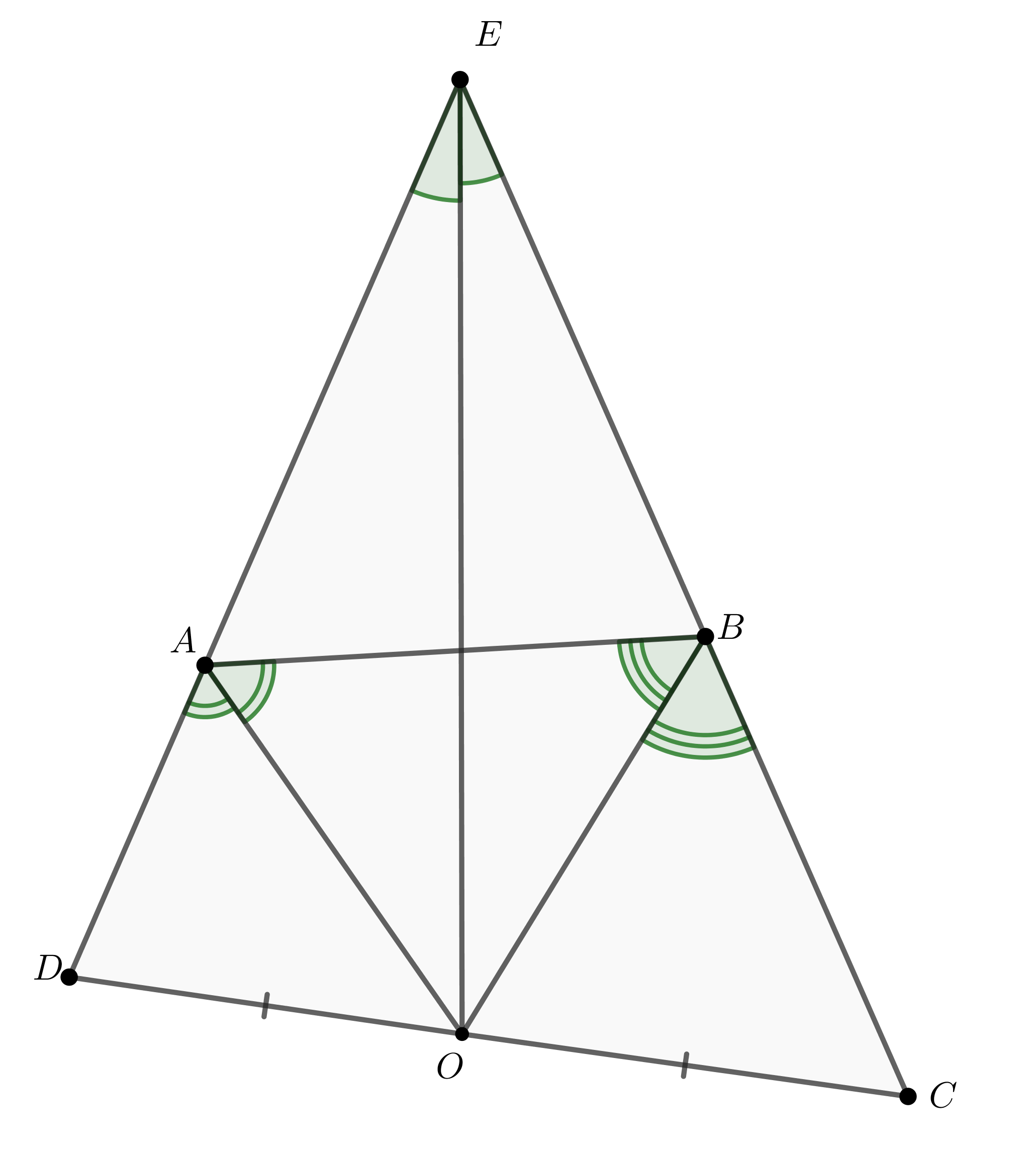
Тогда
— центр вневписанной в
окружности, касающейся стороны
Следовательно,
— биссектриса. Но так как
также является и медианой, то
равнобедренный, следовательно,
- 2.
- Пусть
лежит на продолжении
за точку
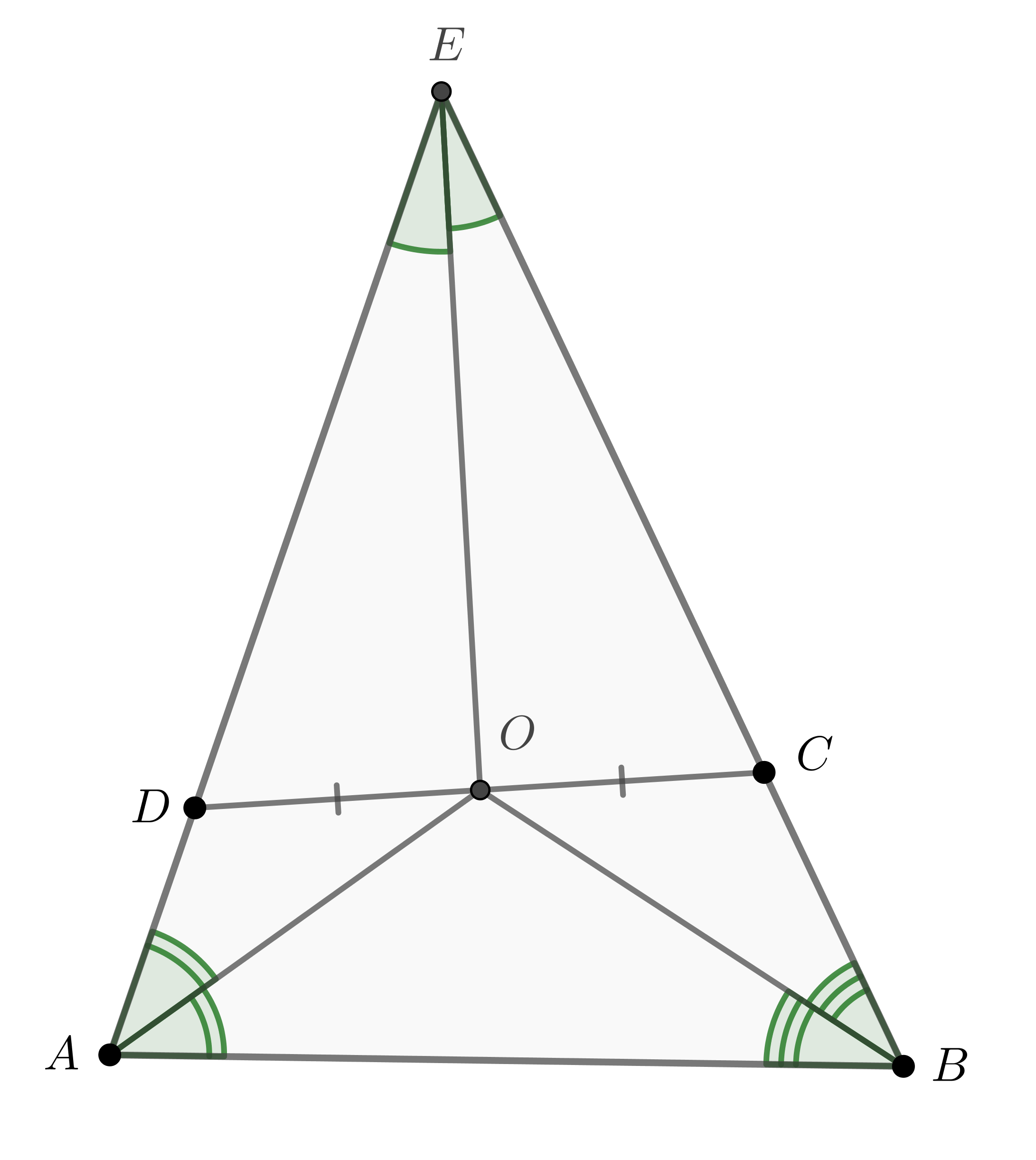
Тогда
— тоска пересечения биссектрис треугольника
следовательно,
— биссектриса угла
Так как
также медиана в
то этот треугольник равнобедренный. Следовательно,
Это внешние углы четырехугольника при вершинах
и
Значит, равны и внутренние углы, то есть
Ошибка.
Попробуйте повторить позже
Стороны угла пересекаются за краем бесконечного листа бумаги (полуплоскости). Как построить след его биссектрисы на листе, не выходя за край?
Рассмотрим два способа.
- 1.
-
Проведем биссектрисы углов
и
, пусть они пересекаются в точке
. На прямой
за точкой
отметим произвольную точку
и проведем через нее прямую, параллельную левой стороне
угла. Пусть эта прямая пересекает правую сторону угла в точке
, то есть
. Построим биссектрису
угла
. Через точку
проведем прямую
. Тогда
— искомый след.
Докажем это. Пусть
— вершина угла. Тогда
как накрест лежащие при
и
секущей. Следовательно, биссектрисы углов
и
также параллельны. А также так как
— точка пересечения биссектрис внешних углов треугольника
при вершинах
и
, то
— центр окружности, вневписанной в
и касающейся стороны
, следовательно,
лежит на биссектрисе угла
. Чтд.
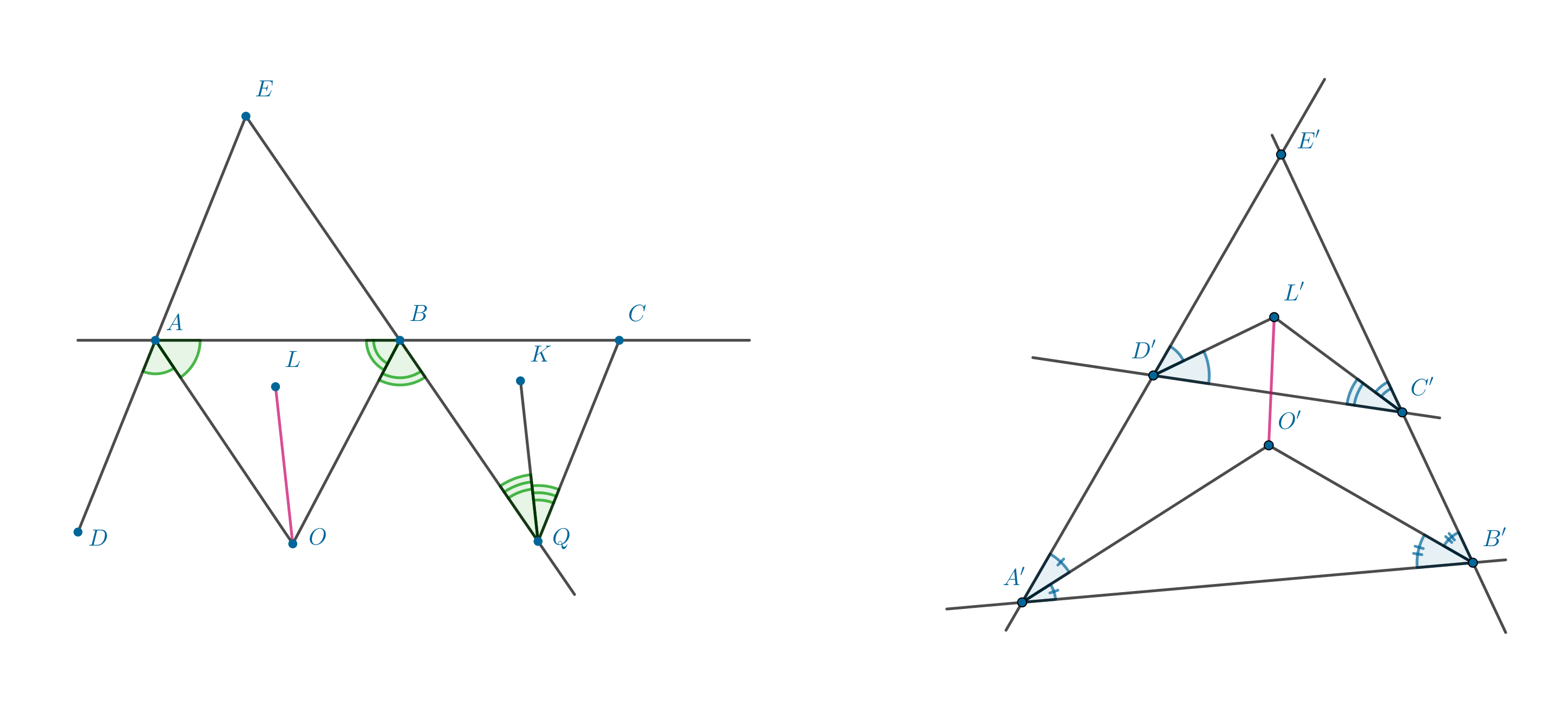
- 2.
-
Произвольно проведем две прямые
и
, пересекающие стороны угла, как показано на рисунке. Получим четырехугольник
. Пусть биссектрисы его внутренних углов
и
пересекаются в точке
, а биссектрисы его внешних углов при вершинах
и
пересекаются в точке
. Тогда
— искомый след.
Докажем это. Пусть
— вершина угла. Так как
— точка пересечения двух биссектрис треугольника
, то
лежит на третьей биссектрисе, то есть на биссектрисе угла
. Аналогично для треугольника
точка
лежит на биссектрисе угла
. Следовательно, точки
и
лежат на биссектрисе угла
. Чтд.
Ошибка.
Попробуйте повторить позже
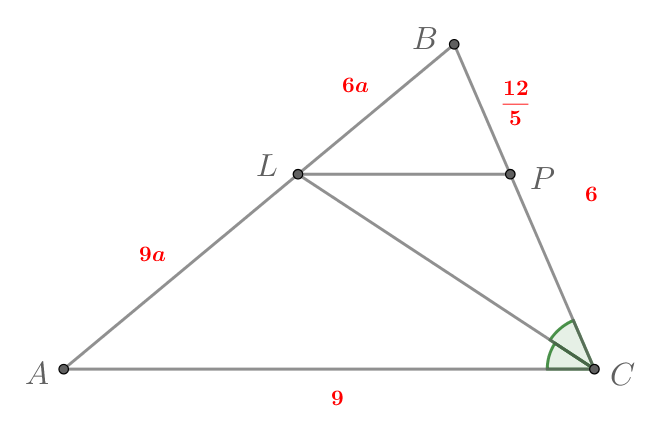
Дан треугольник в котором проведена биссектриса
угла
Через точку
стороны
и точку
стороны
проведена прямая параллельно прямой
Известно, что
Найдите длину отрезка
Так как — биссектриса треугольника
то
Так как то по теореме Фалеса
Пусть
Тогда
следовательно,
Ошибка.
Попробуйте повторить позже
Хорда , хорда
, а хорда
. Точка
– середина дуги
. На какие части
делится хорда
прямой
?
(Источник: Сборник задач по геометрии, И.Ф.Шарыгин, Р.К.Гордин)
Пусть – точка пересечения
и
.
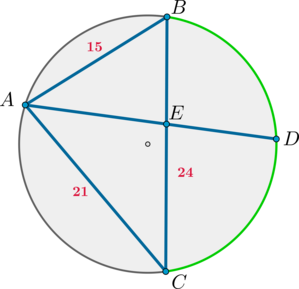
Так как углы и
опираются на равные дуги и оба являются вписанными, то они
равны. Следовательно,
– биссектриса
. Тогда в треугольнике
по свойству
биссектрисы
Ошибка.
Попробуйте повторить позже
В прямоугольном треугольнике с катетами и
проведены биссектрисы острых углов. Найдите
длины этих биссектрис.

По теореме Пифагора найдем гипотенузу . Так как биссектриса треугольника делит его
сторону на отрезки, пропорциональные прилежащим сторонам, то
и
Ошибка.
Попробуйте повторить позже
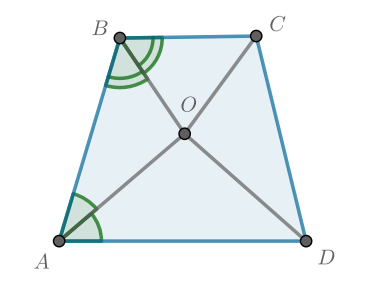
Окружность с центром вписана в трапецию с боковой стороной
Найдите угол
Ответ дайте в
градусах.
Центр вписанной окружности является точкой пересечения биссектрис всех углов. То есть
В трапеции
Тогда по сумме углов треугольника
Ошибка.
Попробуйте повторить позже
В треугольнике известно, что
,
,
. В каком отношении центр
вписанной окружности треугольника делит
биссектрису, проведенную из вершины
?
Центр вписанной окружности треугольника является точкой пересечения биссектрис треугольника. Пусть
— точка пересечения
биссектрисы угла
и стороны
. Рассмотрим треугольник
. Тогда
— биссектриса его угла
. Биссектриса треугольника
делит его сторону на отрезки, пропорциональные двум другим сторонам, значит,
По условию . Найдем
.
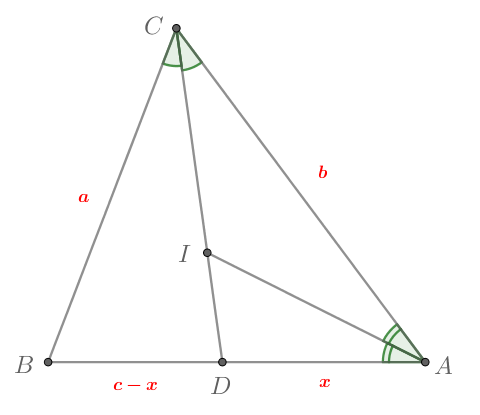
Рассмотрим треугольник . Так как
— его биссектриса, то
С другой стороны, . Пусть
. Тогда
, имеем:
Тогда можем найти искомое отношение:
Ошибка.
Попробуйте повторить позже
Основания трапеции равны 3 и 5 , a ее боковые стороны равны 1 и 2. Каждая из двух окружностей касается трех сторон трапеции. Найдите расстояние между их центрами.
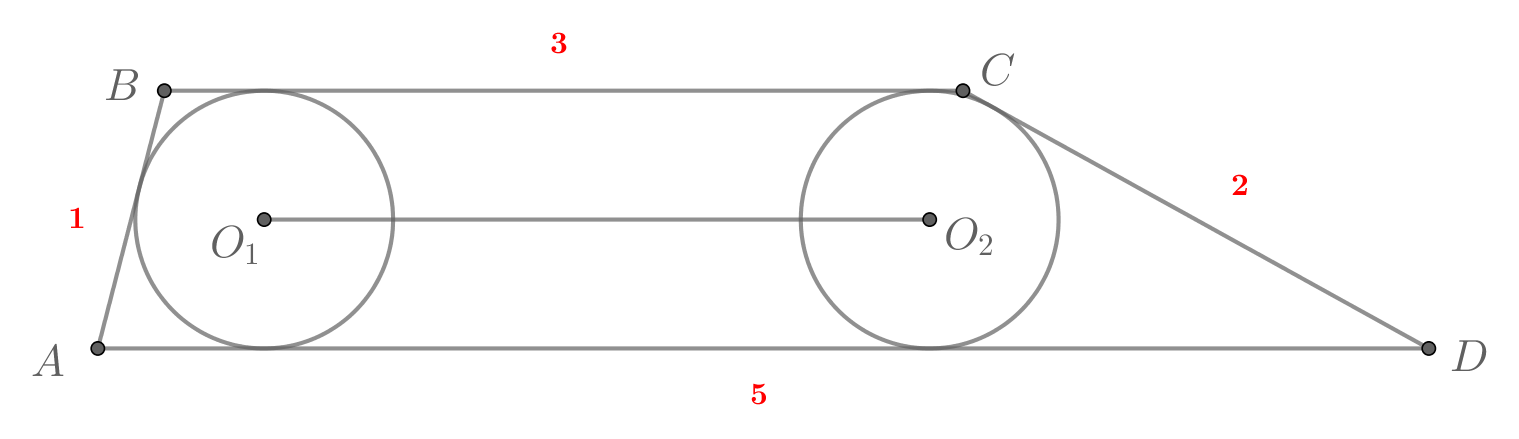
Пусть и
— центры данных окружностей. Рассмотрим треугольник
. В нем
, так как центр
окружности лежит на пересечении биссектрис односторонних углов
и
. Аналогично в треугольнике
имеем
.
Пусть и
— середины боковых сторон
и
соответственно. Тогда
— средняя линия трапеции,
значит,
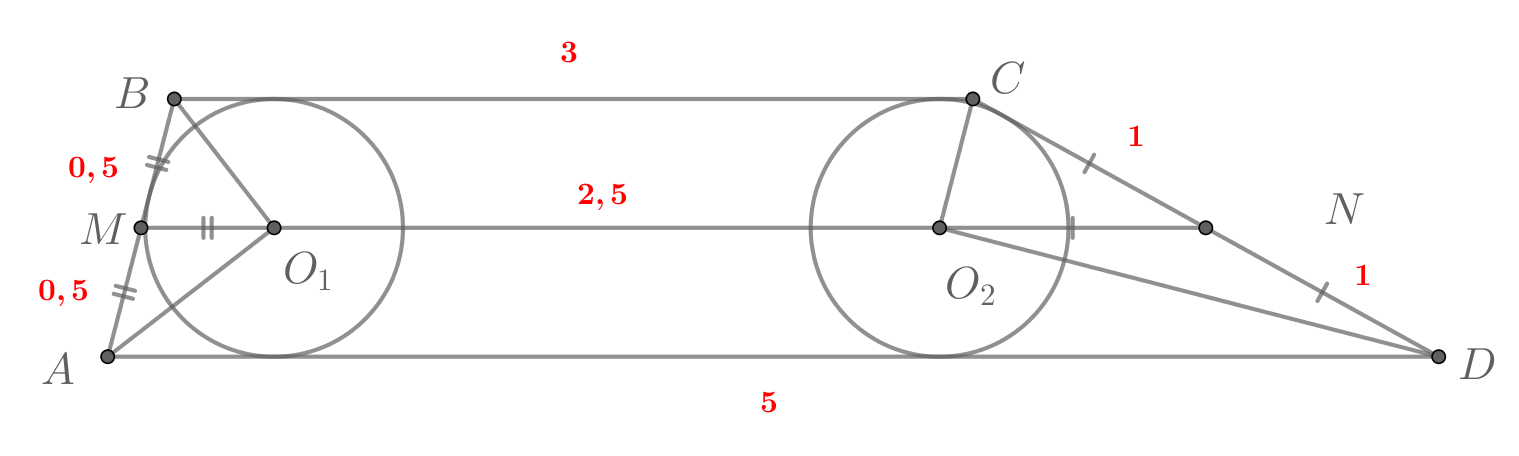
Заметим, что точки и
лежат на средней линии трапеции, так как они равноудалены от оснований трапеции.
Тогда
— середина
, значит,
как медиана прямоугольного треугольника, проведенная к гипотенузе. Аналогично
. Следовательно,
Ошибка.
Попробуйте повторить позже
В четырехугольнике углы
и
равны
. Биссектриса угла
пересекает серединный перпендикуляр к стороне
в точке
. Найдите
.
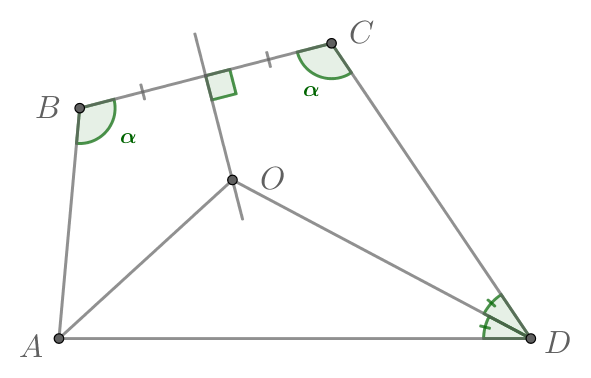
Пусть . Продлим стороны
и
четырехугольника
до пересечения в точке
. Рассмотрим треугольник
. В
нем
, значит, треугольник
— равнобедренный.
В равнобедренном треугольнике на серединном перпендикуляре, проведенном к его основанию, лежат его медиана, высота и биссектриса,
значит, точка лежит на биссектрисе угла
, то есть
равноудалена от прямых
и
. Так как
лежит на биссектрисе
угла
, она равноудалена от прямых
и
, следовательно, точка
равноудалена от прямых
и
, то есть лежит на
биссектрисе угла
.
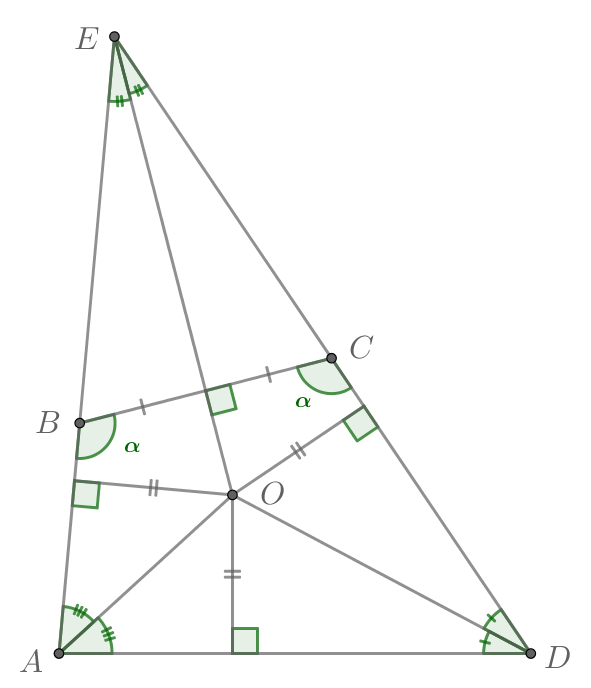
Рассмотрим треугольник . По сумме углов треугольника
По сумме углов четырехугольника
Так как и
— биссектрисы углов
и
соответственно, имеем:
Если , то задача отличается от предыдущей только картинкой, так как все рассуждения не опираются на расположение точки
.
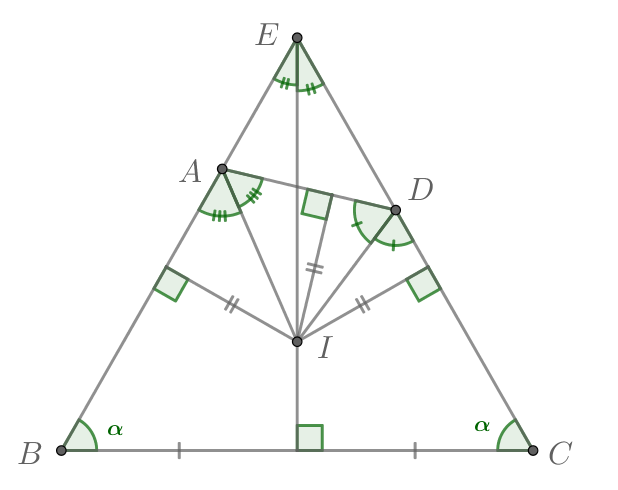
Если , то точка
равноудалена от прямых
и
, так как лежит на прямой, которая параллельна прямым
и
и проходит через середину отрезка с концами на этих прямых. Аналогично предыдущему рассуждению точка
должна лежать на
биссектрисе угла
, тогда угол
можно найти тем же способом.
Ошибка.
Попробуйте повторить позже
От угла равностороннего треугольника со стороной 1 отрезали меньший треугольник так, что биссектриса его внешнего угла делит пополам сторону исходного треугольника, противоположную данному углу. Найдите периметр отрезанного треугольника.
Рассмотрим рисунок. Так как — медиана в равностороннем треугольнике, то она также является и биссектрисой, следовательно,
— центр окружности, вневписанной в треугольник
, касающейся стороны
, то есть
— биссектриса угла
.
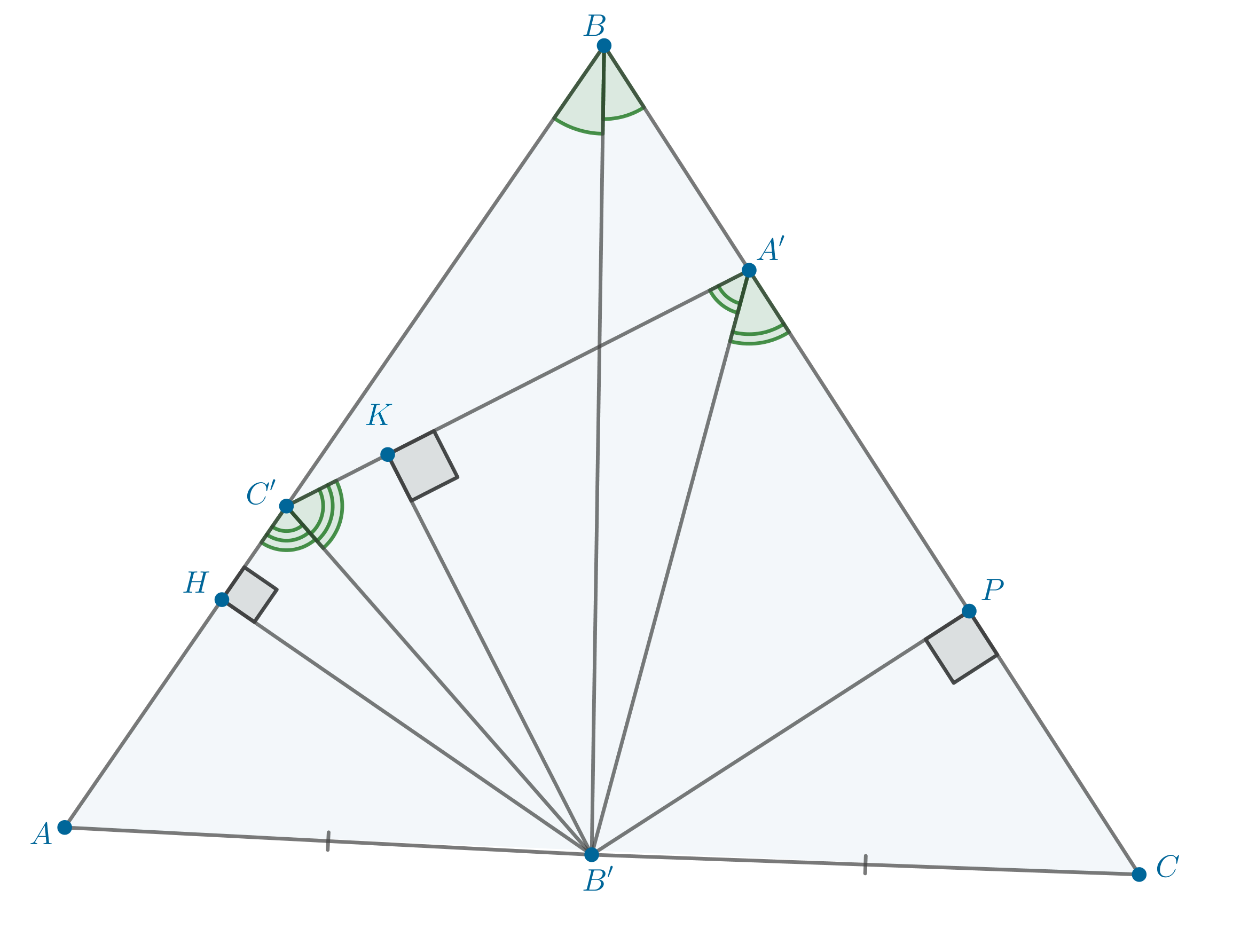
Проведем ,
,
— перпендикуляры к прямым
,
,
соответственно. Эти перпендикуляры равны между собой и
равны радиусу этой окружности. По свойству касательных, проведенных из одной точки к окружности, получаем
,
,
. Следовательно,
.
Так как , то
. Значит,
. Следовательно,
Ошибка.
Попробуйте повторить позже
Дан треугольник , в котором
,
. Проведены биссектриса угла
, пересекающая
в точке
, причем
, и биссектриса внешнего угла при вершине
. Эти биссектрисы пересекаются в точке
. Площадь треугольника
равна
. Найдите расстояние от точки
до прямой
.
Так как — биссектриса в
, то
, следовательно,
. Проведем
и
–
перпендикуляры к прямым
и
соответственно. Так как
— биссектриса угла
, то точка
равноудалена
от сторон этого угла, то есть
. Кроме того, точка
равноудалена от сторон угла
, так как лежит на
биссектрисе этого угла. Тогда искомое расстояние от точки
до прямой
равно
и равно
. Найдем длину
.
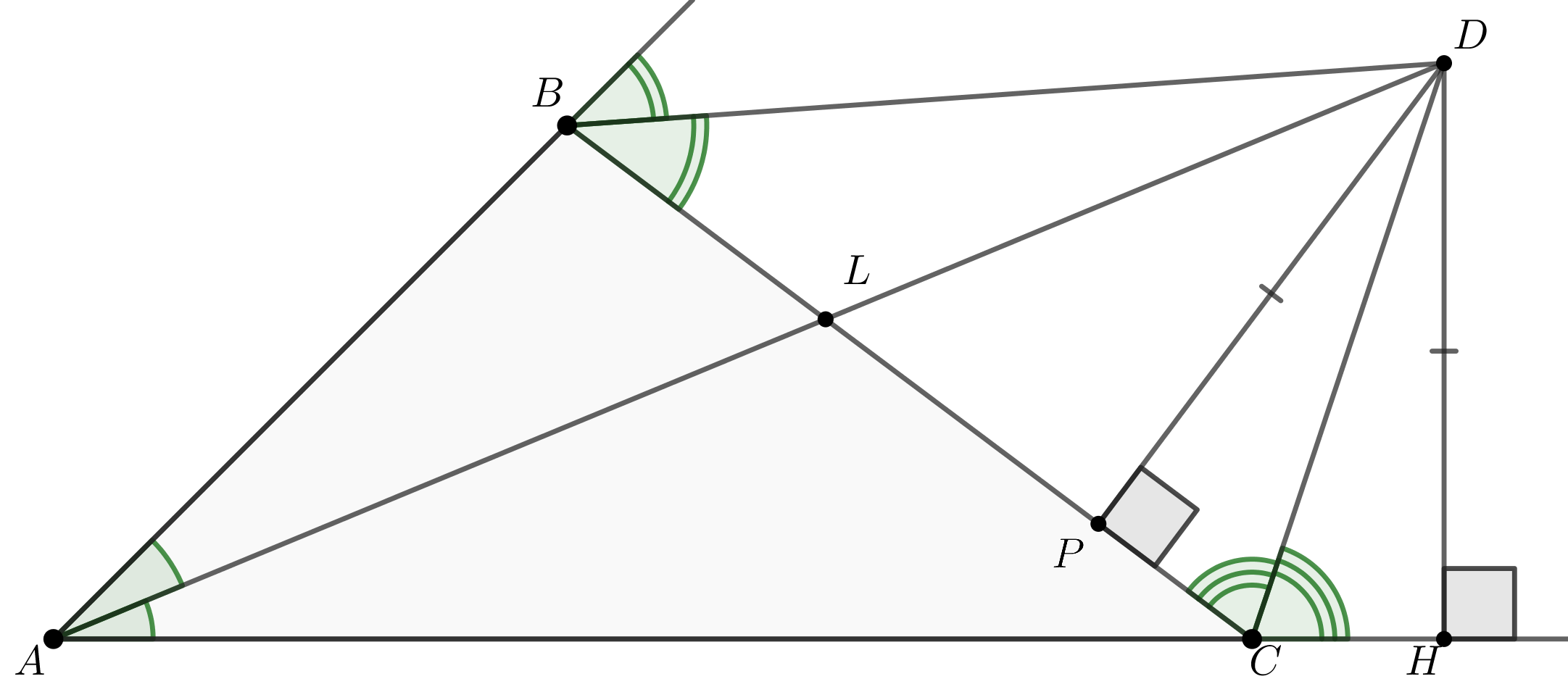
, следовательно,
Ошибка.
Попробуйте повторить позже
В треугольнике с длинами сторон ,
и
проведены биссектрисы, точки пересечения которых с противолежащими сторонами
являются вершинами второго треугольника. Докажите, что отношение площадей второго и исходного треугольников равно
.
Пусть в проведены биссектрисы
,
,
,
,
и требуется доказать, что
где ,
,
.
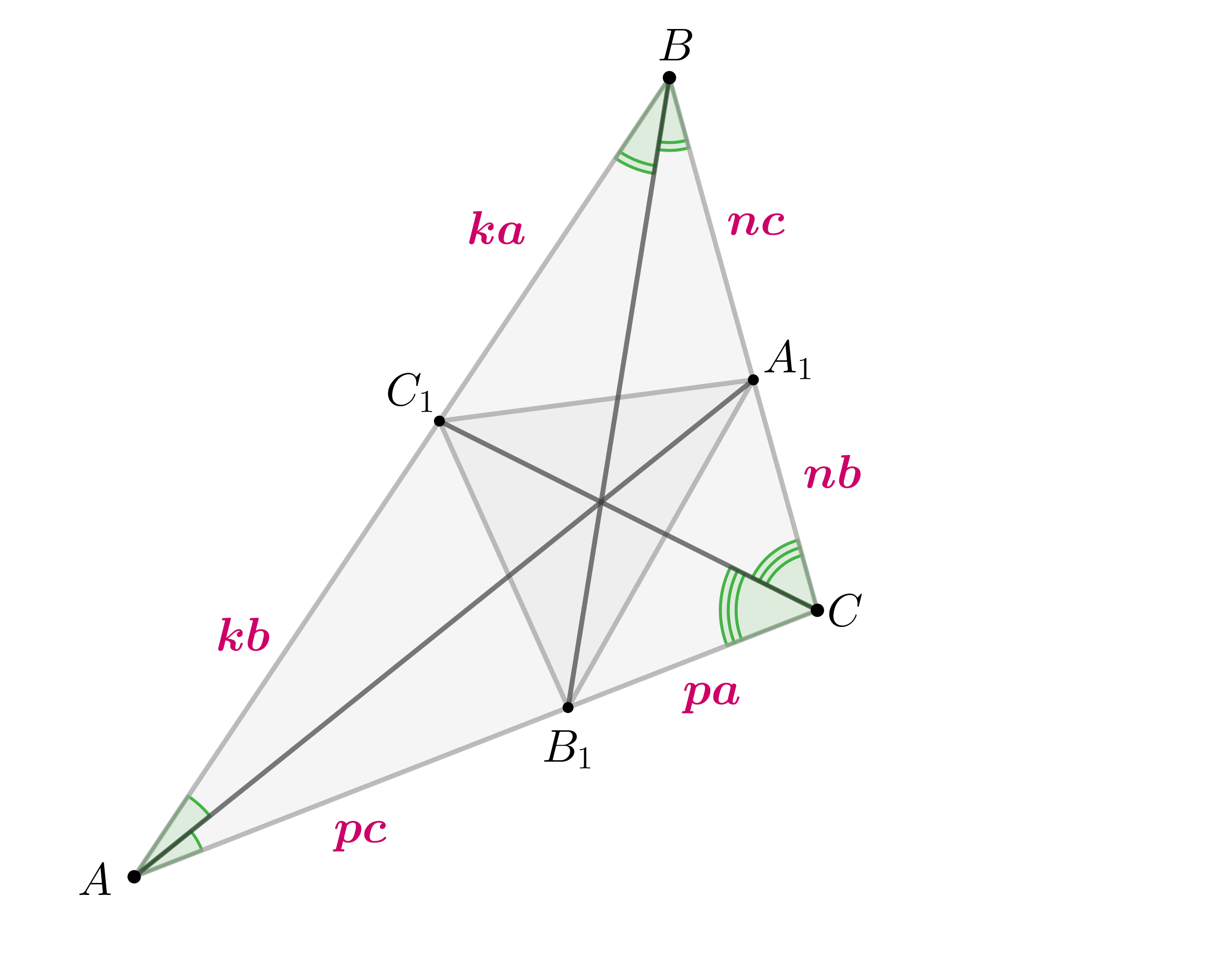
Так как биссектриса угла треугольника делит сторону на отрезки, пропорциональные прилежащим к углу сторонам, то
Тогда можем обозначить ,
,
,
,
,
.
Так как отношение площадей треугольников, имеющих общий угол, равно отношению произведений сторон, образующих этот угол, то
Следовательно, .
Так как , то
. Аналогично
,
. Тогда
Следовательно, . Ч.т.д.



