Раскраски

Предположим, что можно. Разберём два случая:

Случай Пусть Занумеруем столбцы полученного прямоугольника и закрасим все столбцы с номерами вида в красный цвет. Ясно, что любой прямоугольник покрывает ровно красных клеток, а любой прямоугольник покрывает либо либо красных клеток. После потери одного прямоугольника количество красных клеток, покрываемых этими прямоугольниками, уменьшилось на Следовательно, эти клеток должны быть покрыты прямоугольниками Как мы выяснили ранее, такие прямоугольники покрывают либо либо красных клеток, то есть кратно Но мы предположили, что а значит (из равенства ). Таким образом, не может делиться на Противоречие.

Случай Если то Занумеруем строки и покрасим строки с номерами в красный цвет. Далее по аналогичным рассуждениям получим, что кратно Снова пришли к противоречию.

Оценка. Раскрасим доску в цвета, как на рисунке выше: в первой строчке слева направо во второй в третьей снова и так далее. Заметим, что в каждой -тетрамино все клетки разных цветов.

Предположим, что все клетки цвета покрыты хотя бы раз. Тогда всего -тетрамино не меньше То есть на клетки цвета суммарно приходится покрытий. Тогда какая-то из этих клеток покрыта больше раз — противоречие. Значит, есть хотя бы одна непокрытая клетка.

Пример. Расположим -тетрамино (каждое тетрамино выделено своим цветом) в два слоя как на рисунке выше, чтобы все клетки, кроме центральной, были покрыты хотя бы раз (два разных цвета в треугольниках, разделённых диагональю, означают, что клетка покрыта двумя тетрамино).

Если делится нацело то можно разделить всё только на прямоугольники Их будет штук, если обозначить

Если даёт остаток при делении на то обозначим так же и покажем, что делится нацело на

Пронумеруем строки сверху вниз и покрасим строку в цвет остатка её номера по модулю Тогда на доске клеток каждого цвета и клеток каждого цвета

Рассмотрим произвольное разрезание на прямоугольники. Пусть в разрезании участвуют прямоугольников Перекрасим все клетки, покрытые этими прямоугольниками в -ый цвет. Каждый из прямоугольников содержит по одной клетке каждого из цветов. Тогда на доске клеток каждого цвета и клеток каждого цвета которые покрыты фигурами

Заметим, что каждая из фигур покрывает клетки фиксированного цвета. Тогда кратно и кратно Наконец, кратно Значит, в этом случае можно разделить всё на прямоугольники

Покажем, что при существует две эквивалентные раскраски. Покажем, что любую раскраску разрешёнными операциями можно перевести в раскраску, в которой верхний левый квадрат — белый. Действительно, для каждой клетки в квадрате можно подобрать клетки, лежащие вне него так, чтобы они образовывали необходимий прямоугольник. Таким образом, мы можем перекрасить любую клетку. А так как раскрасок, в которых верхний левый квадрат — белый, то по принципу Дирихле найдутся две совпадающих раскраски. Тогда две соответствующие исходные раскраски можно перевести друг в друга.

Покажем, что все раскрасок, в которых верхний левый квадрат — белый, нельзя перевести друг в друга операциями. Заметим, что чётность количества чёрных клеток в -м столбце — инвариант. Аналогичное утверждение верно для строк. А так как в выбранных раскрасках левый верхний квадрат — белый, покраска оставшихся строки и столбца определяет четность количества чёрных клеток во всех строках и столбцах.

Покрасим столбцы фигуры, чередуясь, в черный и белый цвета.

Пусть в Петином разбиении горизонтальных домино и вертикальных домино. Тогда в Васином разбиении тетрамино. Горизонтальные домино содержат одну черную клетку и одну белую и вносят вклад 0 в разность количества черных и белых клеток фигуры. А каждая вертикальная доминошка и каждая -тетраминошка вносит вклад в эту разность.

Но тогда если мы посчитаем разницу черных и белых клеток в фигуре через доминошки и через тетраминошки, то получим, что сумма чисел равна сумме чисел , чего быть не может по модулю 4.

Будем изображать турнир в виде таблицы в которой и столбцы, и строки пронумерованы числами от до Столбцы будут соответствовать девочкам, а строки — мальчикам. Тогда каждая партия задаётся клеткой, координаты которой соответствуют номерам девочки и мальчика, играющих в этой партии. Поставим сначала фишку в клетку После победы девочки фишка будет перемещаться вверх, а в случае победы мальчика — вправо. При этом если фишка доходит до края таблицы, то из последней строки при движении вверх она перемещается в первую строку, а из последнего столбца при движении вправо — в первый столбец. Тогда условие задачи равносильно тому, что фишка обошла все клетки таблицы, побывав в каждой ровно по одному разу.

Раскрасим клетки таблицы в цветов по диагоналям, идущим вправо-вниз: первую диагональ — в первый цвет, вторую — во второй, -ю диагональ — в -й цвет, а следующие диагонали — снова в цвета с первого по -й. Заметим, что после каждой партии номер цвета клетки, в которой находится фишка, увеличивается на по модулю Так как всего в турнире было проведено партий, что кратно то в конце фишка находится в клетке -го цвета, то есть на главной диагонали (далее, говоря «диагональ», мы будем иметь в виду именно эту диагональ). Пусть финальная клетка в маршруте фишки расположена в столбце с номером тогда требуется доказать, что число нечётно.

Из верхней клетки диагонали фишка не могла пойти вверх, так как уже была в клетке Значит, если эта клетка не финальная, то из неё фишка пошла вправо. Тогда и из следующей клетки диагонали она сделала ход вправо, и т.д. до клетки, расположенной в столбце с номером Аналогично из клеток диагонали, находящихся в столбцах с номерами от до фишка ходила вверх. Пусть первая клетка диагонали, в которую попала фишка, находится в столбце с номером Рассмотрим путь фишки от начальной клетки до неё. Все пути от клеток первого цвета до следующей клетки -го цвета должны быть такими же, как и рассматриваемый путь, а именно, каждый такой путь получается из другого смещением на вектор Действительно, если бы фишка из клетки сделала ход вверх, а из клетки — вправо, то в клетку она бы не попала, а если из этих клеток она делала ходы вправо и вверх соответственно, то попала бы в одну клетку дважды; поэтому из каждых двух таких клеток фишка делала одинаковые ходы.

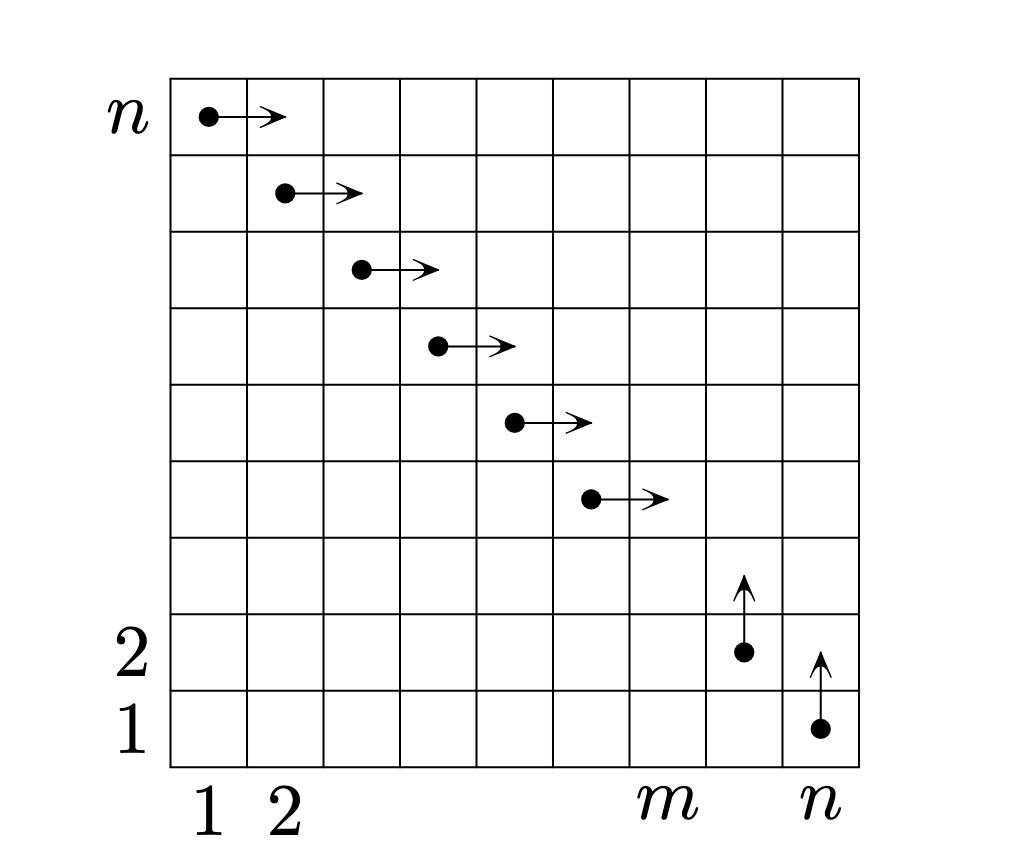
Без ограничения общности будем считать, что Клетки диагонали, находящиеся левее финальной клетки, будем называть левыми, а находящиеся правее — правыми. Пронумеруем левые клетки числами от до а правые — от до (и те, и другие нумеруем, двигаясь вправо-вниз). Посмотрим, в каком порядке фишка обходила эти клетки. С левых клеток она смещалась на клеток вправо (поскольку с них в клетку первого цвета она делала ход вправо), а с правых клеток — на клетку вправо. Значит, для левых клеток нам важен лишь остаток от деления номера на а для правых — от деления на При этом, если правых клеток меньше то можно увеличить на добавив правых клеток; это не повлияет на дальнейшие рассуждения. Для удобства заменим все номера клеток на соответствующие остатки, причём для правых клеток вместо остатка будем использовать число

Пусть число при делении на даёт остаток Тогда первый переход с левых клеток на правые был с числа на число и в этот момент все клетки с нулём в левой части были посещены. На диагонали остались только числа от до Дальше цепочка переходов между правыми и левыми клетками выглядит так:

В этой цепочке каждое число от до встречается два раза, начинается она на правых клетках, а заканчивается на левых. Переходы с правых клеток на левые будем называть переходами первого типа, а с левых на правые — второго. Тогда в цепочке переход первого типа и перехода второго, и они чередуются.

Докажем, что каждые два числа в цепочке, симметричные относительно её центра, дают в сумме Для крайних чисел это верно. Каждые два симметричных перехода имеют один тип, поэтому в них по модулю (для переходов первого типа) или по модулю (для переходов второго типа) прибавляется одно и то же число. Значит, сумма следующих двух симметричных чисел (которые ближе к центру цепочки) снова равна либо по модулю либо по модулю Но сумма самих чисел не меньше и не больше поэтому она может быть равна только

Предположим, что число чётно, и рассмотрим два случая.

1) Число нечётно. Тогда центральный переход в цепочке имеет второй тип. У правой нижней клетки диагонали нечётный номер, поскольку число нечётно, а чётно. Левая верхняя клетка диагонали тоже имеет нечётный номер, поэтому при переходе первого типа чётность числа меняется. Пусть с числа переход первого типа происходит на число Тогда по модулю переходы первого типа выглядят так: …, Суммы чисел в этих парах являются последовательными нечётными числами, поэтому при делении на они дают все нечётные остатки по два раза. В частности, есть переход, в котором сумма чисел равна по модулю Как показано выше, эта сумма равна Но тогда для этого перехода симметричный ему тоже имеет первый тип и содержит те же самые числа, то есть один из переходов повторился, чего быть не должно.

2) Число чётно. Тогда у центрального перехода в цепочке первый тип. Последняя левая клетка имеет нечётный номер, так как число нечётно, а чётно. У первой правой клетки тоже нечётный номер, значит, при переходе второго типа чётность числа не меняется. Аналогично первому случаю можно показать, что среди них найдётся переход, пара чисел в котором даёт сумму и получаем такое же противоречие.

Раскрасим доску в шахматном порядке. Тогда ладья каждым ходом меняет цвет клетки, на которой она стоит. Значит, спустя 111 ходов ладья окажется на клетке, отличной по цвету от изначальной. Но на доске цвета угловой клетки и центральной совпадают, противоречие.

В этой задачке раскраска уже не дает противоречия. Давайте просто оценим количество ходов, которое нужно ладье, чтобы попасть в центральную клетку из угловой. Ей нужно сделать минимум 55 ходов по горизонтали и столько же по вертикали, то есть в сумме хотя бы 110 ходов. Но она сделала только 88 — поэтому дойти до центральной клетки не может.

Заметим, что чётные и нечётные клетки на пути Лизы чередуются: из нечётной клетки Лиза всегда прыгает в чётную, а из чётной — в нечётную. При этом начинала Лиза с нечётной клетки, а закончила в чётной. Это значит, что на нечётных клетках Лиза побывала столько же раз, сколько на чётных. В нечётных клетках Лиза побывала раз. В чётных раз, где  — количество раз, которое Лиза была в клетке номер 10. Тогда .

Разобьем все клетки граней кубика на группы примыкающих к одной из вершин куба (то есть в каждой группе будут находиться три клетки, примыкающие к фиксированной вершине куба). Заметим, что в каждой группе все три клетки будут раскрашены в разные цвета. Следовательно, количество квадратов одного цвета одного цвета не превосходит

Осталось привести пример. Уберем из рассмотрения любые две противоположные грани куба. Клетки оставшихся граней можно раскрасить в шахматном порядке. Если мы выберем среди них только черные клетки и покрасим их в черный цвет, а все остальные квадраты — в разные цвета, то получим требуемый пример.

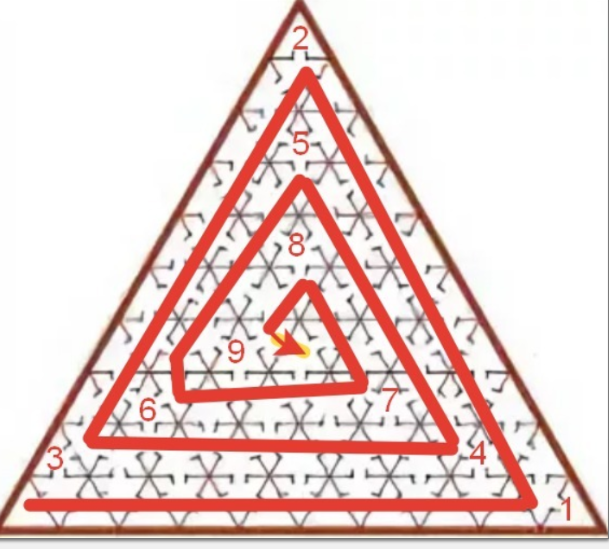
Раскрасим замок в шахматном порядке (вдоль каждой стороны цвета чередуются). Тогда каждая дверь соединяет два зала разных цветов. Посчитаем количество залов каждого цвета. Выберем сторону, вдоль которой будем считать, и заметим, что залов одного цвета на первой линии ровно 1, на второй — 2, на третьей — 3, на последней — 10. Значит, первого цвета у нас , а второго — . Так как турист чередует цвета залов, то он может посетить не более зал.

Теперь осталось придумать пример на 91.

Раскрасим доску в шахматном порядке.

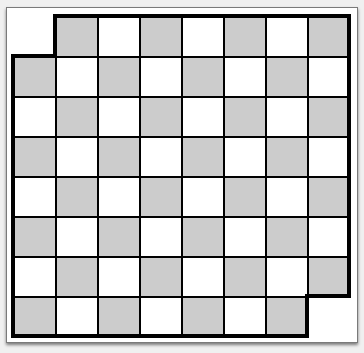
Заметим, что обе вырезанные клетки одного цвета, пусть, не умаляя общности, белого. Тогда в оставшейся доске остается черных клетки и белых. Но каждая доминошка занимает одну белую и одну черную клетки, значит, больше доминошек из оставшейся доски мы не вырежем. А так как клеток осталось то доминошек при разрезании должно получиться чего не может быть.

Сначала отметим, что шахматная раскраска здесь вряд ли поможет: она не различает вертикальные и горизонтальные доминошки, ведь и в тех, и в других одна белая и одна черная клетки. Поэтому поищем раскраску, при которой вертикальные и горизонтальные доминошки все же различаются.

Раскрасим шахматную доску вертикальным матрасиком в два цвета. При такой раскраске любая горизонтальная доминошка содержит по одной белой и черной клетке, а вертикальная — либо белых и черных, либо наоборот, белых и черных. Поэтому горизонтальных доминошек покроют черных клеток, а вертикальных — еще некоторое четное количество. Значит, всего будет покрыто нечетное количество черных клеток. А при данной раскраске черных клеток , противоречие.

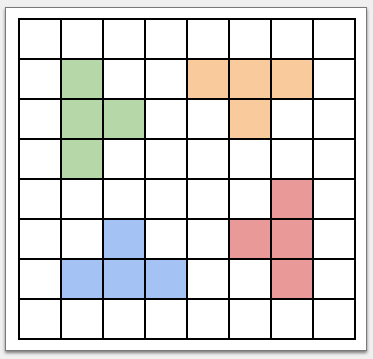
Предположим, что указанное разрезание все-таки возможно. Тогда в нем должно быть T-тетрамино. Покрасим доску в шахматном порядке в белый и черный цвета и заметим, что любая T-тетрамино занимает клетки одно цвета и другого. Поэтому тетрамино покроют нечетное количество количество белых клеток. Меж тем белых клеток при такой раскраске всего то есть четное число. Значит, указанное покрытие невозможно.

Замечание. Также можно заметить, что T-тетрамино не могут покрывать поровну черных и белых клеток, что тоже ведет к противоречию.

Первое решение.

Предположим противное и покрасим доску в горошек:

Заметим, что один прямоугольник покрывает либо либо черных клеток, то есть четное количество. Значит, прямоугольники покроют четное число черных клеток. Но в указанной раскраске их штук, значит, покрыть все черные клетки по одному разу невозможно.

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение.

Предположим противное и покрасим доску матрасиком:

Горизонтальные прямоугольники занимают две белые и две черные клетки. А вертикальные могут занимать либо белых, либо черных клетки. Так как всего черных и белых клеток поровну, то и черных прямоугольников будет столько же, сколько и белых. Таким образом, вертикально расположенных прямоугольников на доске четное количество.

Перекрасим доску в горизонтальные полоски. Рассуждая аналогично, получим, что количество горизонтально расположенных прямоугольников тоже чётно. Таким образом, общее число всех прямоугольников на доске — четно. Но, если бы можно было разрезать доску на прямоугольники то прямоугольников должно было быть штук. Но — нечетное. Получили противоречие, значит, доску нельзя разрезать на прямоугольники

______________________________________________________________________________________________________________________________________________________

Третье решение.

Разделим доску на квадраты размером и раскрасим их в черно-белые цвета в шахматном порядке:

Видно, что белых клеток на больше. Прямоугольник занимает на доске две белые и две черные клетки. Если нам удастся разрезать квадрат на прямоугольники то цветов должно быть поровну, но у нас белых клеток больше — противоречие.

_________________________________________________________________________________________________________________________________________________________________________________

Четвёртое решение.

Предположим противное и покрасим доску диагонально в цвета:

Тогда любой прямоугольник покрывает ровно по клетке каждого цвета. Если нам удастся разрезать квадрат на прямоугольники, то всех цветов на доске будет поровну. Легко сосчитать, что клеток второго цвета а четвертого а должно было быть поровну — противоречие.

Предположим, что указанное разрезание возможно, и из доски вырезана правая верхняя угловая клетка. Раскрасим доску в три цвета так, чтобы нетронутая главная диагональ была целиком покрашена в один цвет (оранжевый).

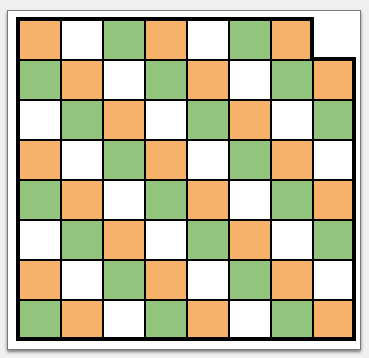
Заметим, что при такой раскраске количество зеленых и белых клеток отличается на , так как в раскраске доски их поровну, а вырезанная клетка белая. При этом каждый прямоугольник занимает по одной клетке каждого цвета. Значит, одновременно все белые и все зеленые клетки по одному разу покрыть нельзя, поэтому и всю доску разрезать на прямоугольники не удастся.

Нарисуем квадратную доску размеров на и раскрасим, как указано в условии.

Несложно видеть, что на этой картинке белых клеток.

Раскрасим доску в диагональную раскраску в три цвета. Заметим, что из цвета мы в любом случае идем в цвет с цвета — в цвет с цвета — на цвет Поскольку клеток цвета больше всех ( а не ), мы должны начать и закончить на цвете

(a) Раскрасим клетки в шахматную раскраску. Заметим, что после команды все жуки из белых клеток переползут в чёрные, а из чёрных — в белые. На доске чёрных и белых клеток. Значит, какие-то два жука переползут из чёрных клеток в одну белую.

(b) Пометим клетки как показано на рисунке:

Из верхнего левого угла жук переползёт во вторую слева клетку четвёртой строки, а из верхнего правого угла — во вторую справа клетку четвёртой строки. Также понятно, что из средней клетки верхней строки жук переползёт либо во вторую слева, либо во вторую справа клетку в четвёртой строке, то есть в одной из этих клеток будет два жука.

Покрасим доску в шахматную раскраску. Заметим, что из чёрной клетки конь попадает в белую, а из белой — в чёрную. То есть цвета клеток при проходе должны чередоваться. Так как мы должны вернуться в начальную клетку, то клеток каждого цвета должно быть поровну. Но на доске белые клетки и чёрных, а значит, мы не сможем обойти всю доску и вернуться в начальную клетку.