14.07 Перпендикулярность. Доказательство базовых фактов
Ошибка.
Попробуйте повторить позже
Боковые ребра пирамиды равны между собой. Докажите, что высота пирамиды проходит через центр окружности, описанной около основания.
Рассмотрим треугольную пирамиду , где
,
— высота. Докажем, что
— центр описанной около
окружности.
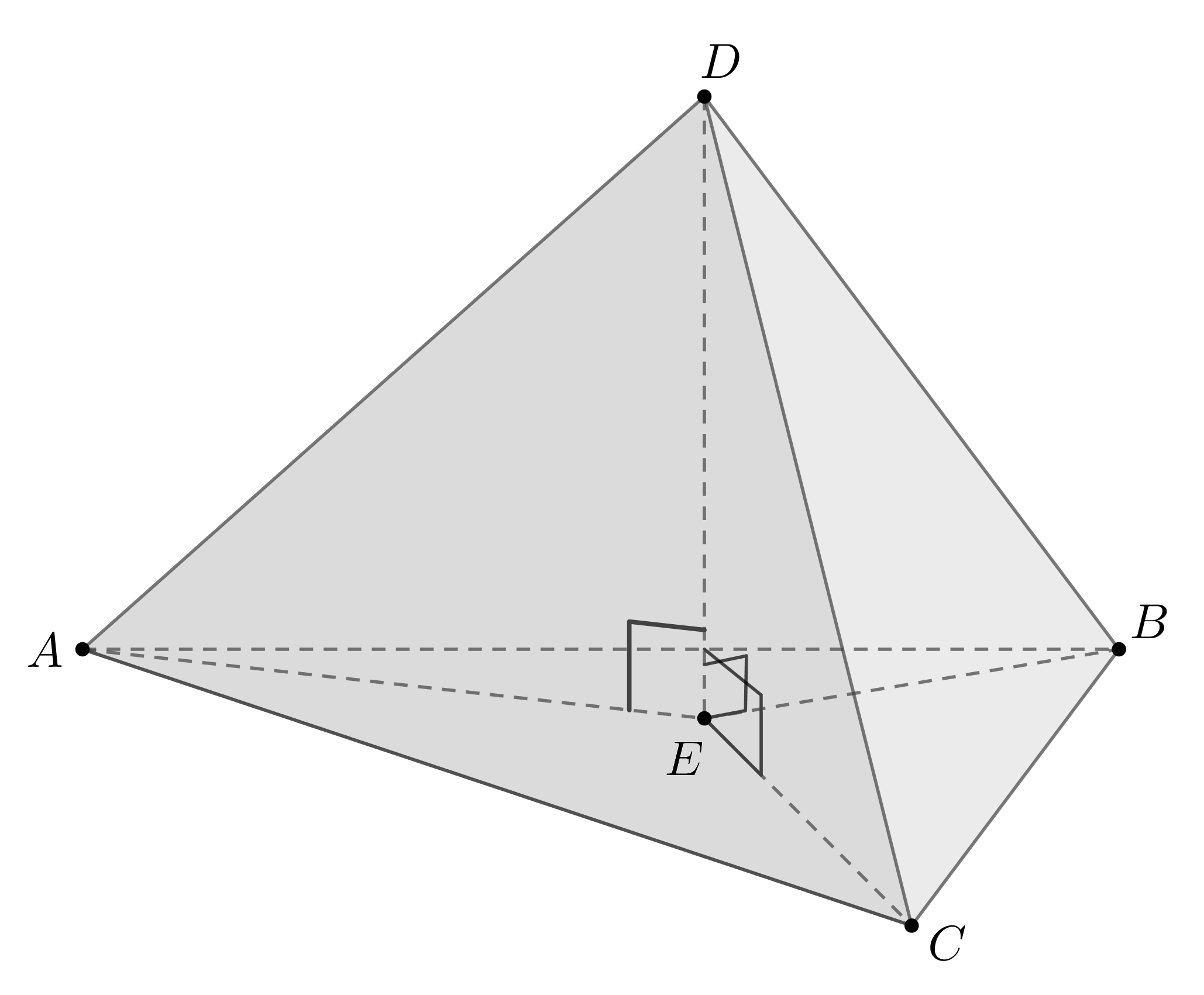
Так как то
перпендикулярна любой прямой из плоскости
, следовательно,
—
прямоугольные и общим катетом
. Так как
, то
по катету и гипотенузе. Следовательно,
. Следовательно,
равноудалена от вершин
, следовательно, по определению является центром описанной
окружности.
Доказательство для производной пирамиды аналогично с единственной разницей, что равных треугольников будет не 3, а столько же, сколько вершин в основании этой пирамиды.
Ошибка.
Попробуйте повторить позже
Докажите, что если одна из двух параллельных прямых перпендикулярна некоторой плоскости, то и вторая прямая перпендикулярна этой плоскости.
Докажите, что верно и обратное: две прямые, перпендикулярные одной и той же плоскости, параллельны.
Прямой факт:
Пусть даны ,
,
,
. Требуется доказать, что
.
Через две параллельные прямые проходит плоскость, и притом только одна. Следовательно, проведем через и
плоскость
. По
признаку перпендикулярности двух плоскостей
.
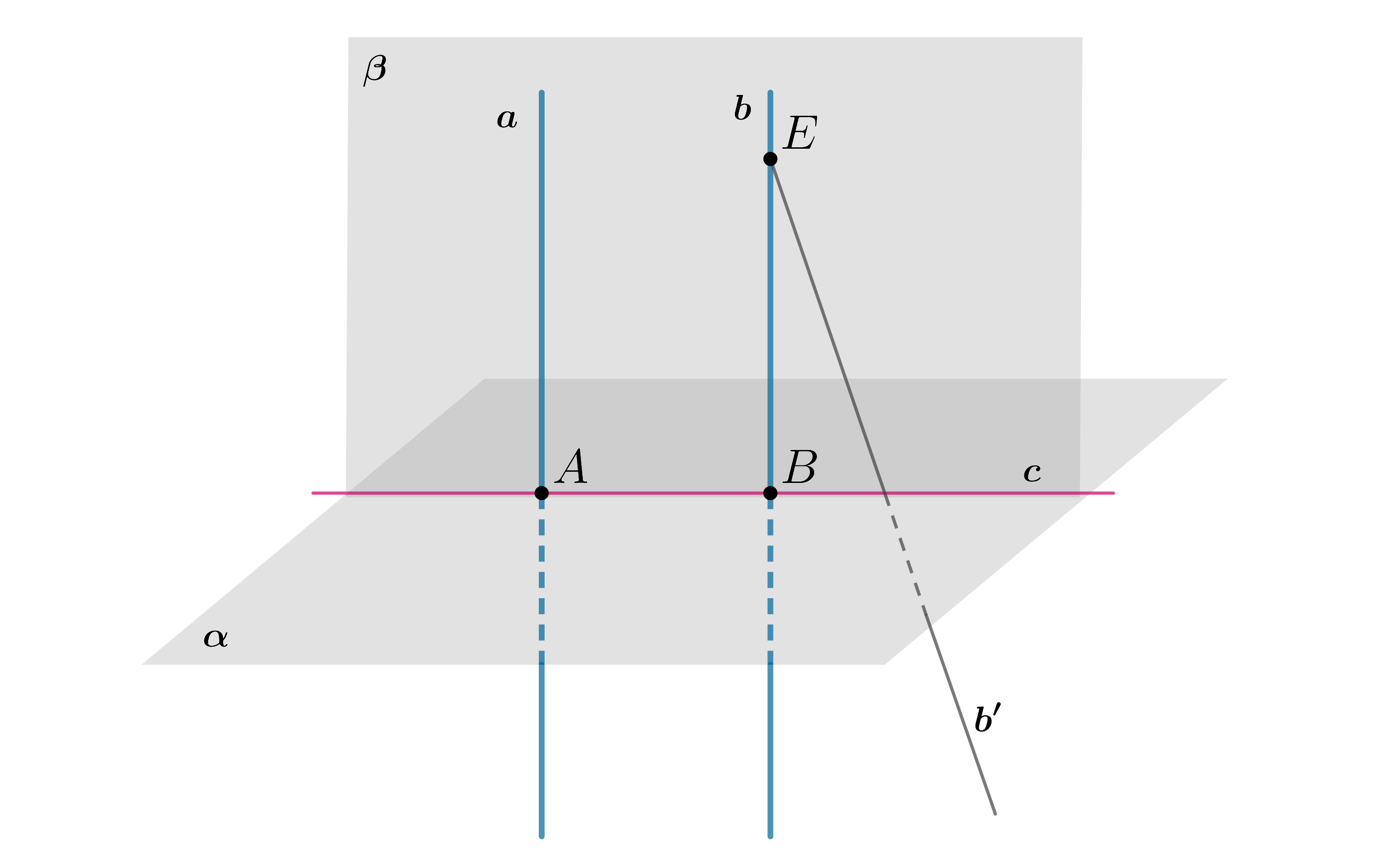
Из построения следует, что прямая , она же прямая
, есть линия пересечения плоскостей
и
. Пусть
не перпендикулярна
. Проведем через точку
прямую
в плоскости
. Тогда
перпендикулярна любой прямой из
, следовательно,
.
Так как
и
лежат в одной плоскости (как две пересекающиеся прямые) и перпендикулярны прямой из этой плоскости, то они
параллельны. Получили противоречие с тем, что
Обратный факт:
Прямые в пространстве могут быть параллельны, пересекаться или скрещиваться.
- 1.
. Пусть
,
,
,
.
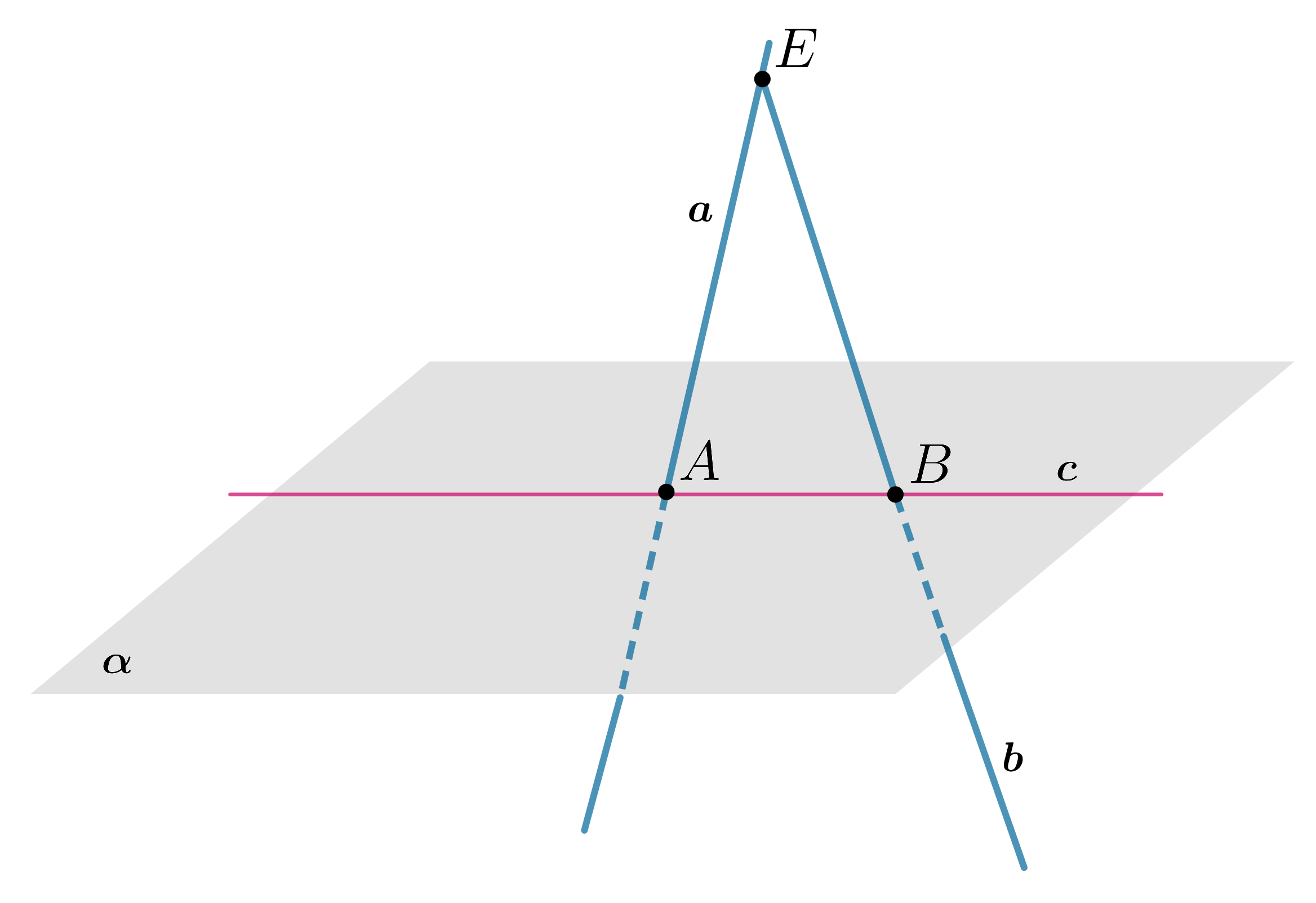
Тогда
. Три точки
образуют плоскость
, в которой лежат прямые
(так как лежат две точки каждой прямой в этой плоскости). Но в плоскости если две прямые перпендикулярны третьей, то они параллельны, следовательно,
. Противоречие.
- 2.
. Пусть
,
,
,
.
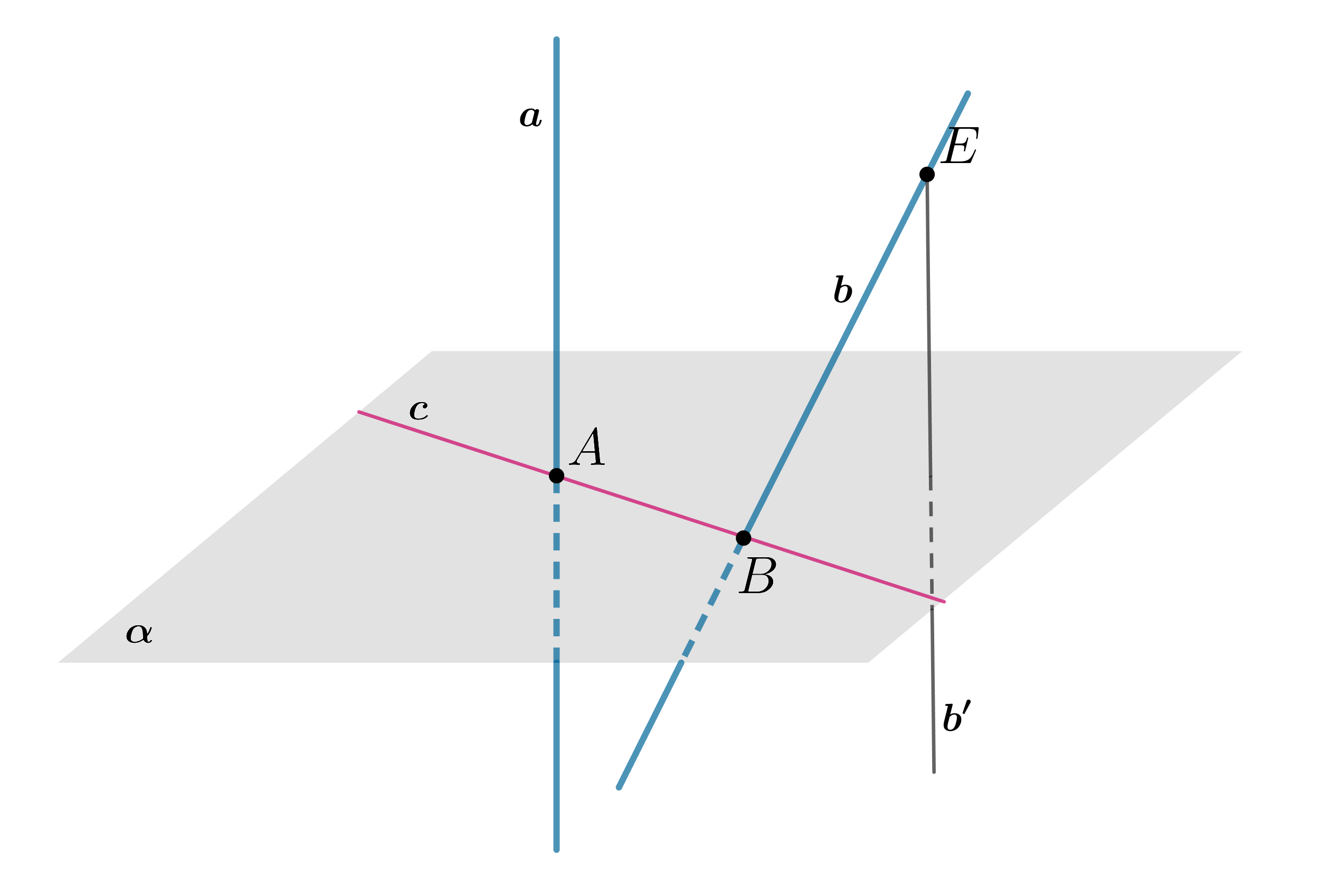
Через точку
прямой
проведем прямую
. По прямому факту получаем, что
. Следовательно, получаем пункт 1., который невозможен.
Чтд.
Ошибка.
Попробуйте повторить позже
Докажите, что прямая, лежащая в плоскости, перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна (ортогональной) проекции этой наклонной на данную плоскость.
(теорема о трех перпендикулярах: прямая и обратная)
Прямая: если прямая перпендикулярна проекции
прямой
на
, то
Дана наклонная ,
, следовательно, по определению
— проекция
Так как
, то прямая
перпендикулярна двум пересекающимся прямым
и
, следовательно,
, откуда следует, что
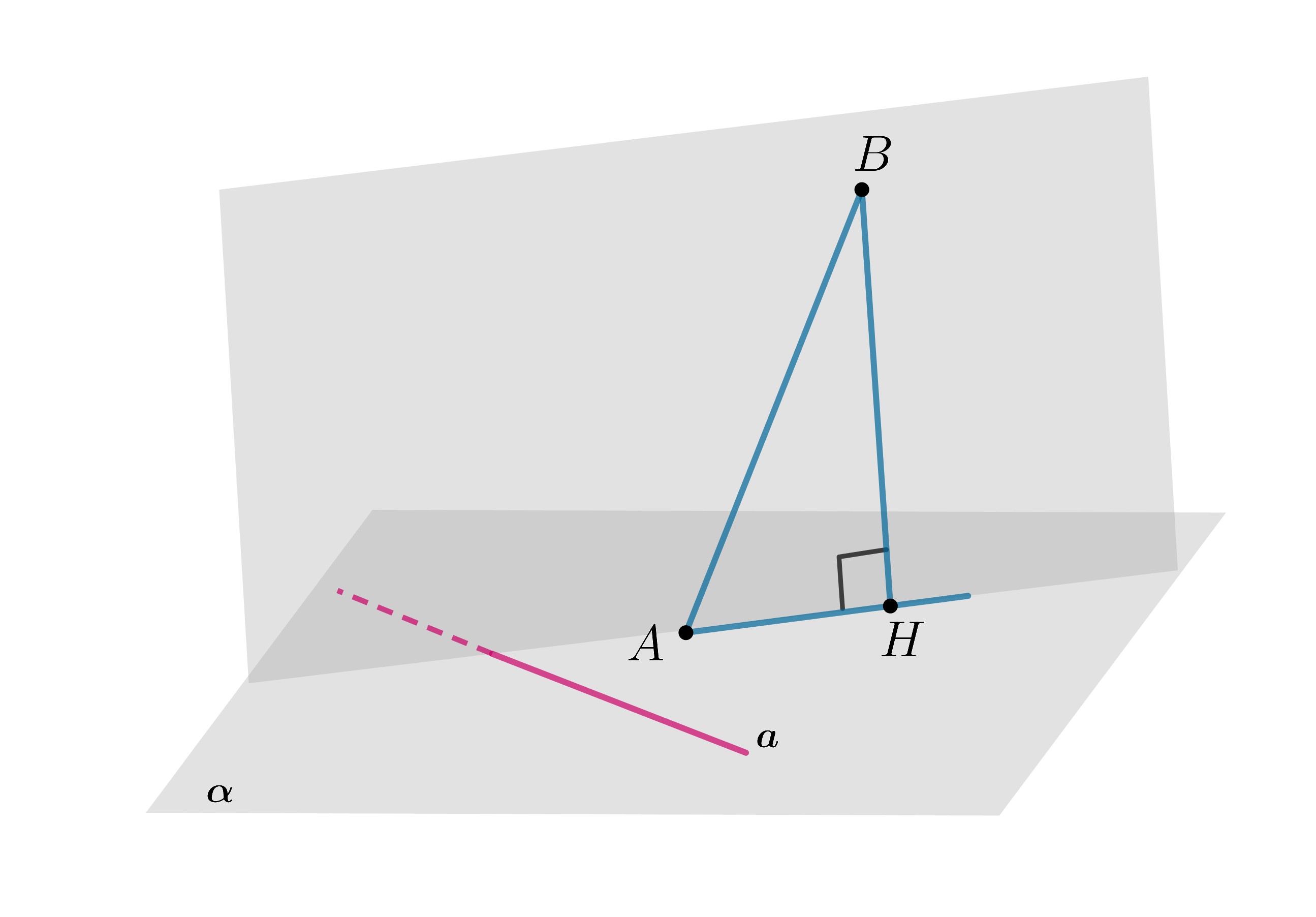
Обратная: если прямая перпендикулярна наклонной
к плоскости
, то она перпендикулярна и проекции
прямой
на
эту плоскость.
Так как , то прямая
перпендикулярна двум пересекающимся прямым
и
, следовательно,
, откуда
следует, что
Ошибка.
Попробуйте повторить позже
Докажите, что если прямая, лежащая в некоторой плоскости, перпендикулярна двум пересекающимся прямым, одна из которых лежит в той же плоскости, то одна из данных двух прямым является проекцией второй прямой на эту плоскость.
Пусть ,
,
. тогда
.
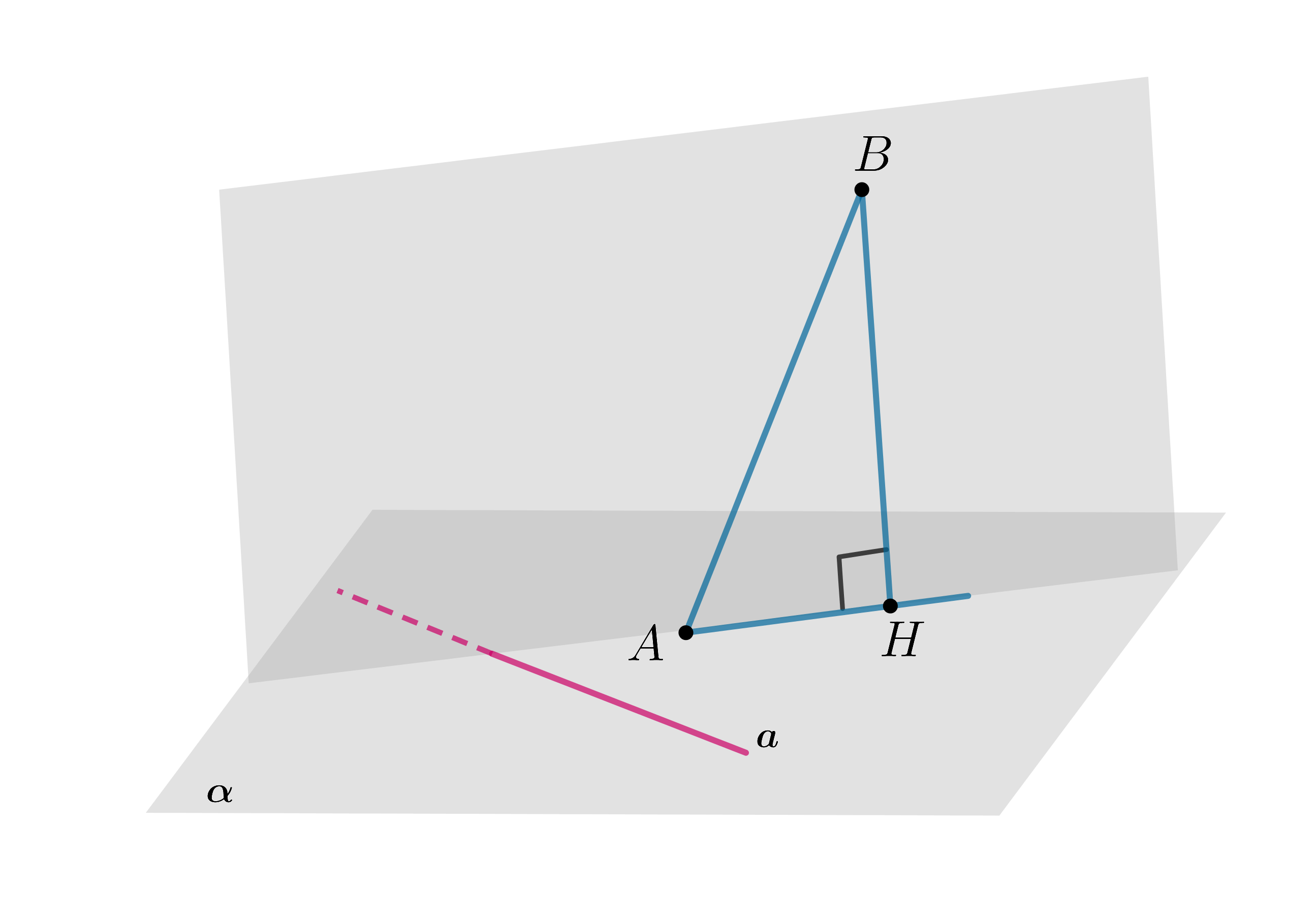
Выберем на прямой точку
таким образом, чтобы
. Так как
то
. Следовательно,
,
то есть двум перпесекающимся прямым плоскости
, значит,
Ошибка.
Попробуйте повторить позже
Верно ли, что две прямые, перпендикулярные одной и той же прямой, параллельны?
Пусть . Без ограничения общности можно считать, что
пересекают
в точках
и
соответственно (если какая-то прямая
не пересекает
то проведем прямую, параллельную ей, пересекающую
). Через прямую
и точку
можно провести плоскость.
Заметим, что
имеет с этой плоскостью одну общую точку – точку
, следовательно,
может как лежать в этой плоскости,
так и пересекать ее. Если
лежит в этой плоскости, то по теореме для плоскости “если две прямые перпендикулярны
третьей, то они параллельны” имеем
. Если же
пересекает эту плоскость, то по признаку скрещивающихся прямых
.
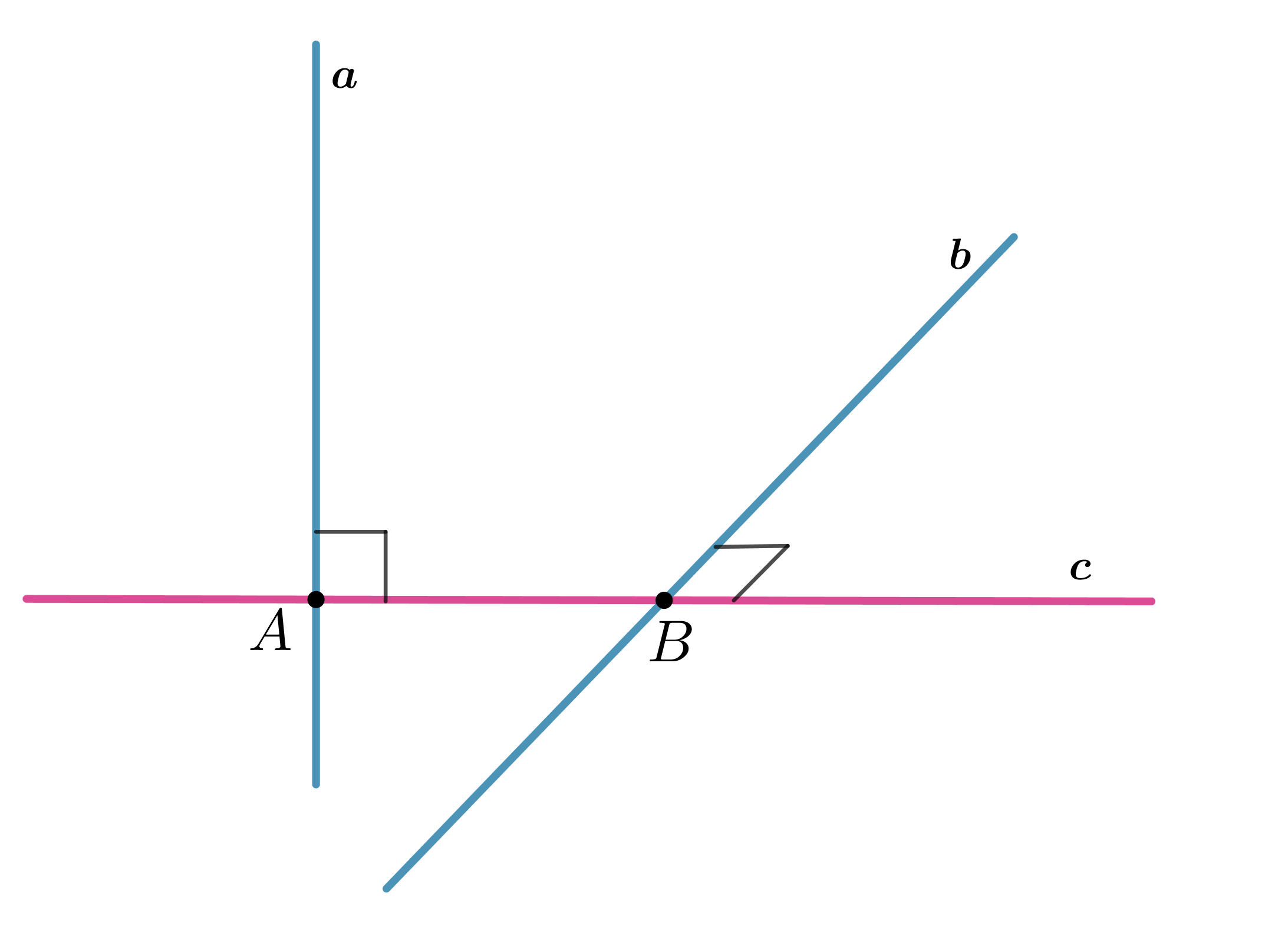
Следовательно, ответ: нет.
Ошибка.
Попробуйте повторить позже
Докажите, что через одну из двух перпендикулярных скрещивающихся прямых можно провести единственную плоскость, перпендикулярную другой.
(полезный факт при нахождении расстояния между перпендикулярными скрещивающимися прямыми)
Пусть Проведем через некоторую точку
прямую
. Так как
, то через них проходит плоскость
, и притом
только одна.
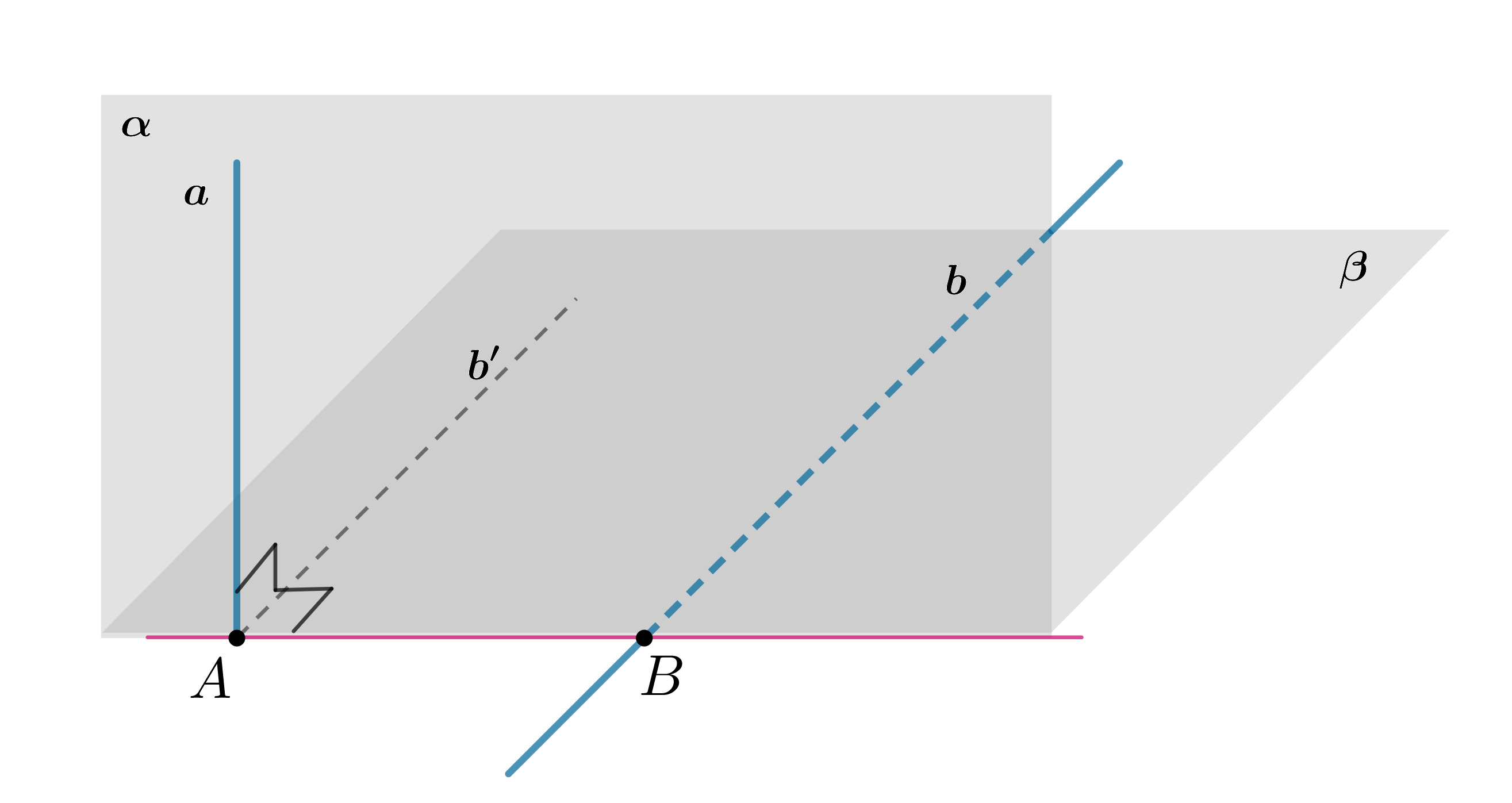
В плоскости проведем
. Тогда плоскость
, проходящая через две пересекающиеся прямые
и
, будет искомой
плоскостью. Она единственна, так как через две пересекающие прямые проходит единственная плоскость, и она перпендикулярна
, так
как
.
Ошибка.
Попробуйте повторить позже
Известно, что некоторая точка равноудалена от двух перпесекающихся прямых
и
. Докажите, что ортогональная
проекция точки
на плоскость прямых
и
лежит на биссектрисе одного из углов, образованных прямыми
и
Пусть , прямые
и
лежат в плоскости
Пусть
— перпендикуляры на прямые
и
соответственно.
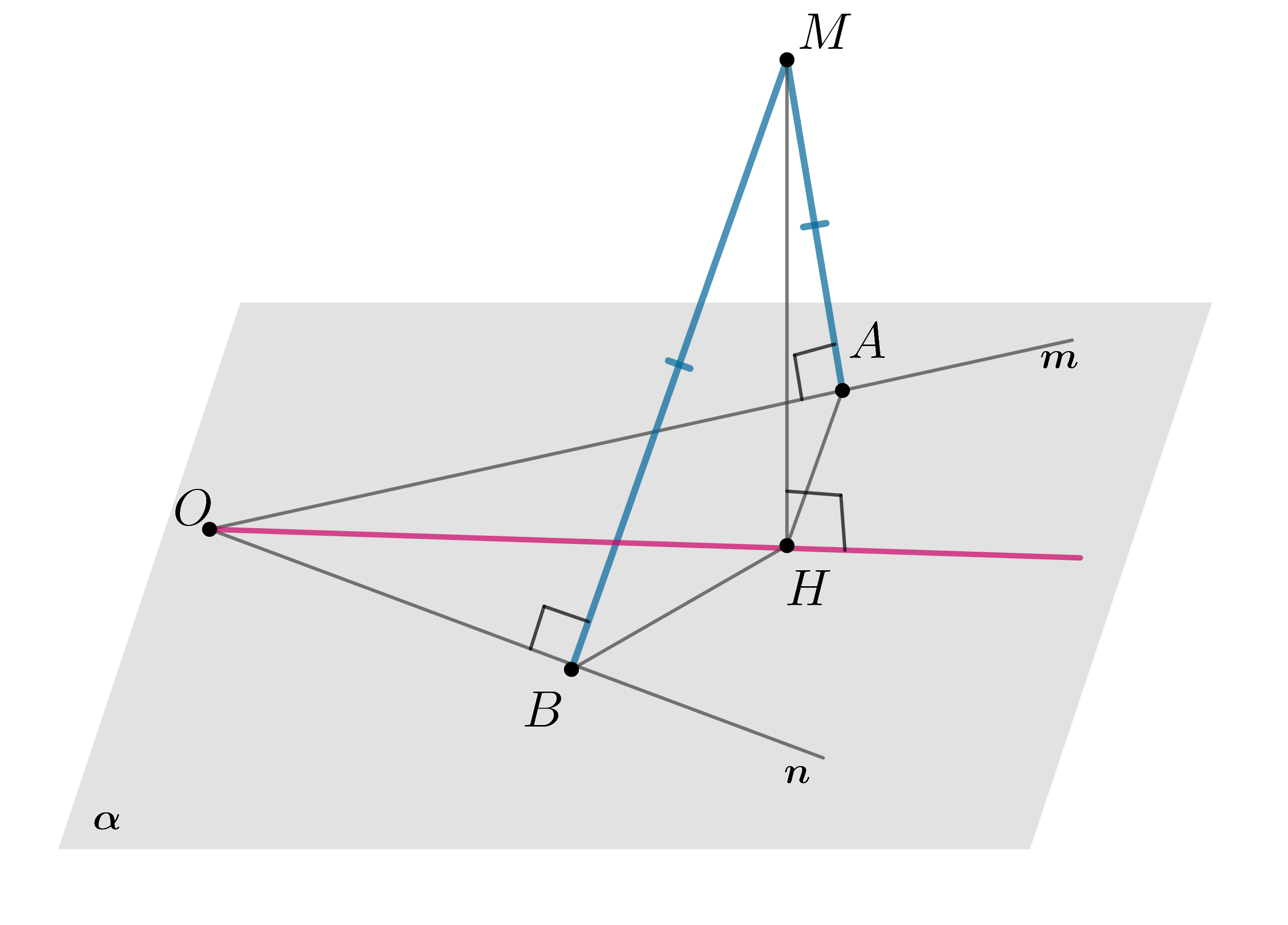
Проведем . Тогда по обратной ТТП проекция
, проекция
. Также
как прямоугольные по
общему катету
и гипотенузе
. Следовательно,
. Тогда
— точка, равноудаленная от сторон угла
,
следовательно, лежит на его биссектрисе.
Ошибка.
Попробуйте повторить позже
Пусть
— четыре точки в пространстве, не лежащие в одной плоскости. Докажите, что если
то прямые
и
перпендикулярны.
По условию получаем, что — тетраэдр. Проведем высоты к основаниям равнобедренных треугольников
и
Тогда основание каждой высоты — это середина основания. Следовательно, если
— середина
то
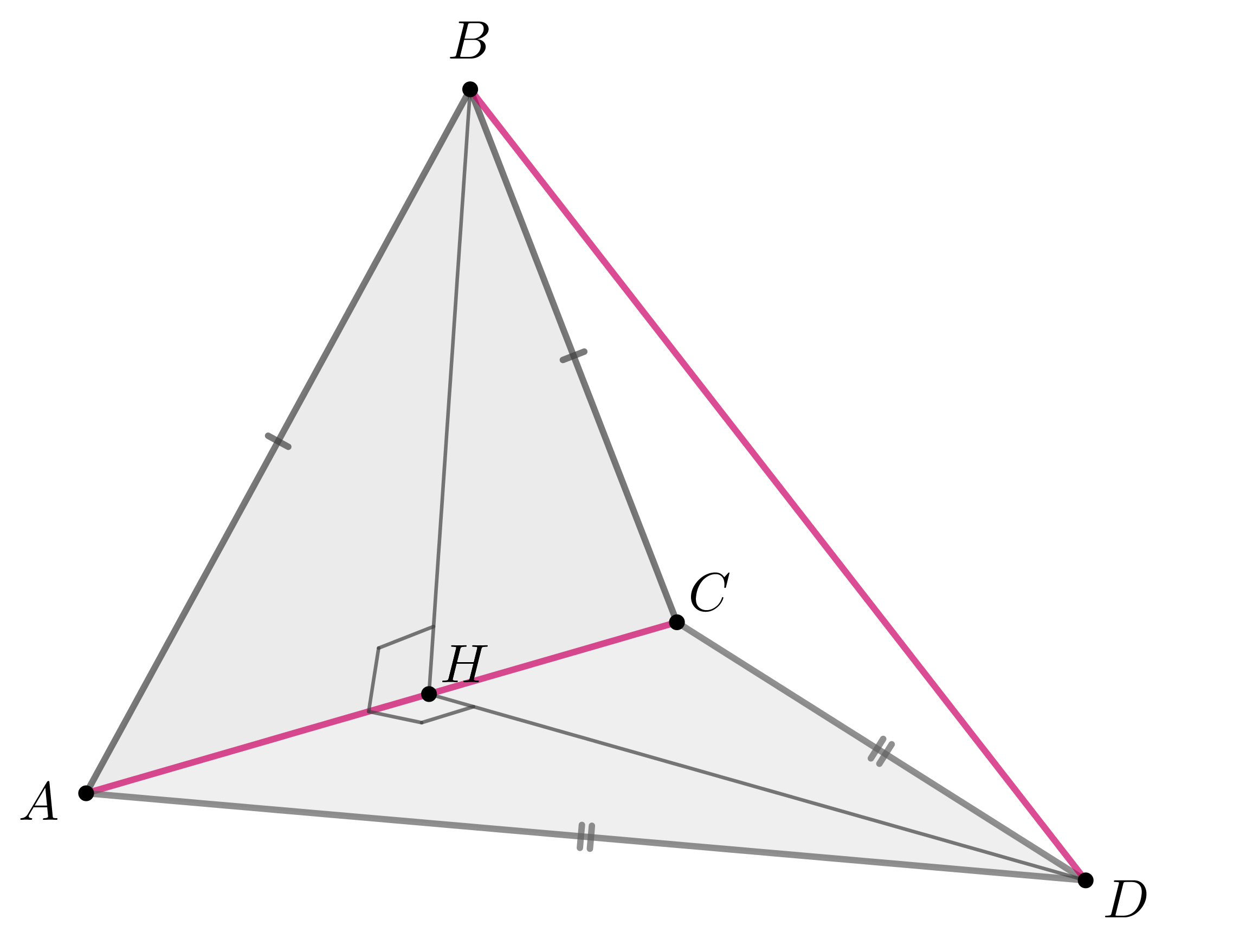
Тогда так как перпендикулярна двум пересекающимся прямым плоскости
Следовательно,
перпендикуляна любой прямой из этой плоскости, откуда
Ошибка.
Попробуйте повторить позже
Докажите, что ГМТ, равноудаленных от двух заданных точек пространства, есть плоскость, перпендикулярная отрезку с концами в этих точках и проходящая через его середину.
Пусть дан отрезок и две точки
, равноудаленные от точек
и
Тогда
и
лежат на серединных перпендикулярах
и
соответственно к отрезку
. Отсюда получаем, что
, следовательно, плоскость, в которой лежат точки
, проходит через середину
отрезка
и перпендикулярна ему.
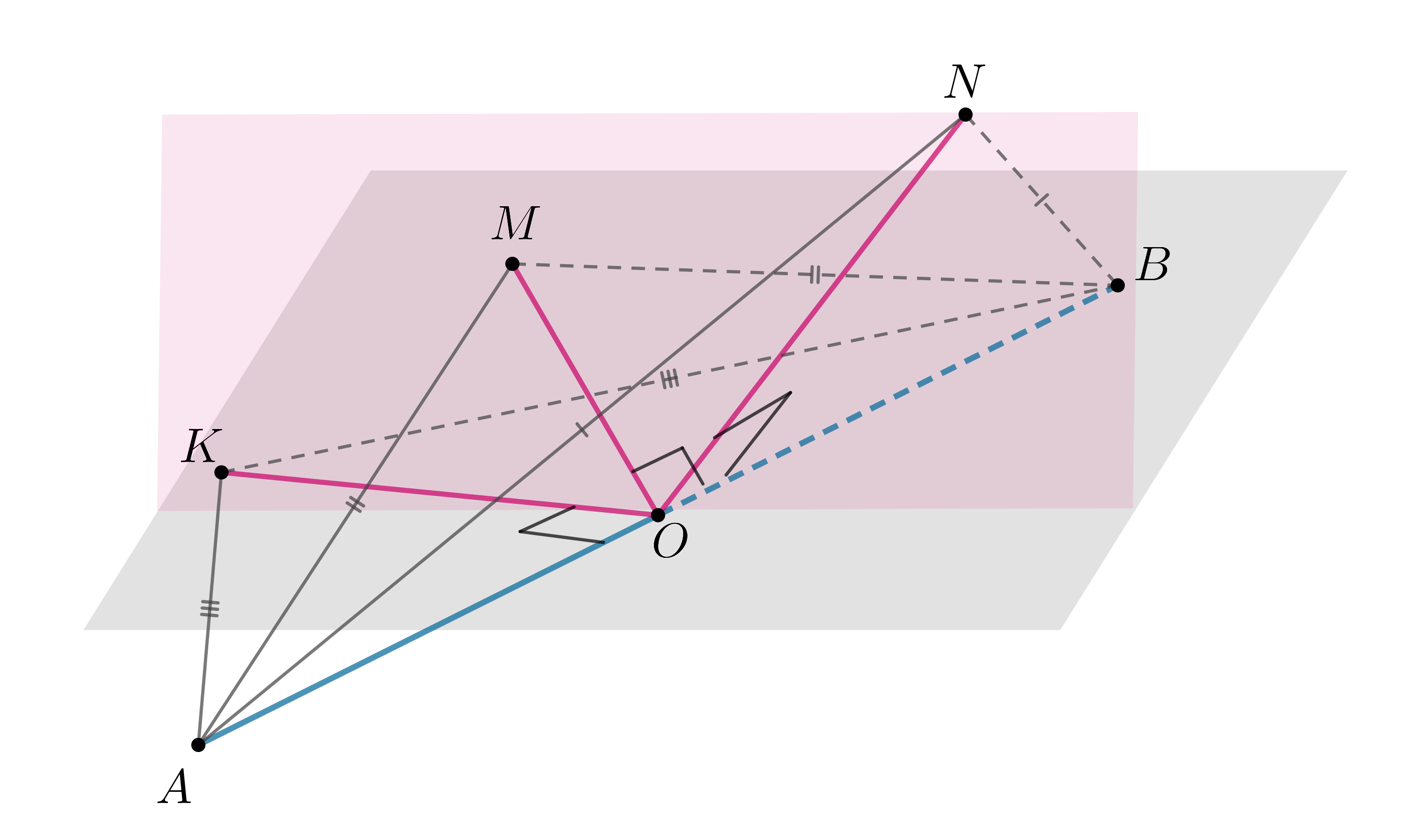
Докажем, что другая точка , равноудаленная от
и
будет лежать в этой плоскости. Аналогично
, тогда
. Тогда плоскости
и
совпадают, как две пересекащиеся плоскости, перпендикулярные одноой
прямой.
Докажем, что любая точка плоскости равноудалена от концов отрезка
Возьмем точку
,
—
середина
, следовательно, в
отрезок
— высота и медиана, следовательно,
равнобедренный, то есть
Ошибка.
Попробуйте повторить позже
Даны две скрещивающиеся прямые и
и плоскость
, перпендикулярная прямой
и пересекающаяся ее в точке
Докажите, что
расстояние между прямыми
и
равно расстоянию от точки
до ортогональной проекции
прямой
на плоскость
, а угол
между прямыми
и
дополняет до
угол между прямыми
и
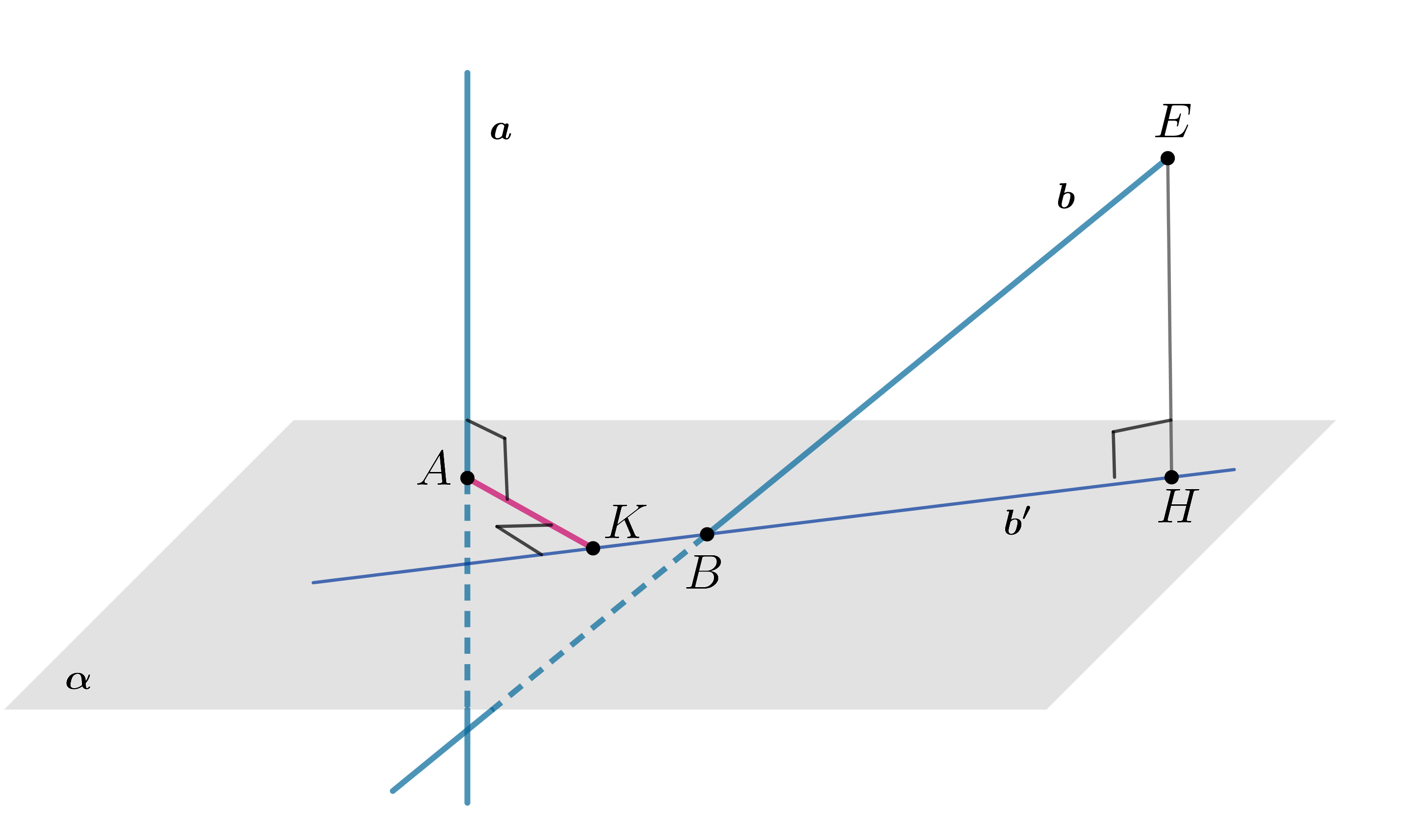
Рассмотрим два случая:
- 1.
Проведем из некоторой точки
прямой
прямую
, следовательно,
Отсюда следует по определению, что
— проекция
на плоскость
Проведем
. Тогда
, следовательно,
, следовательно,
. Но также
, так как
перпендикулярна любой прямой, лежащей в
Следовательно,
— общий перпендикуляр к двум скрещивающимся прямым
и
Чтд.
Так как
, то
Чтд.
- 2.
Тогда
Далее построение аналогично построению в предыдущем пункте.
Ошибка.
Попробуйте повторить позже
Даны три попарно перпендикулярные прямые. Четвертая прямая образует с данными прямыми углы соответственно. Докажите,
что
Пусть прямые попарно перпендикулярны. прямая
образует с ними углы
соответственно. Проведем
,
,
. Если отметить на
отрезки
,
,
, то получим прямоугольный параллелепипед
, диагональ которого равна
, а ребра равны
.
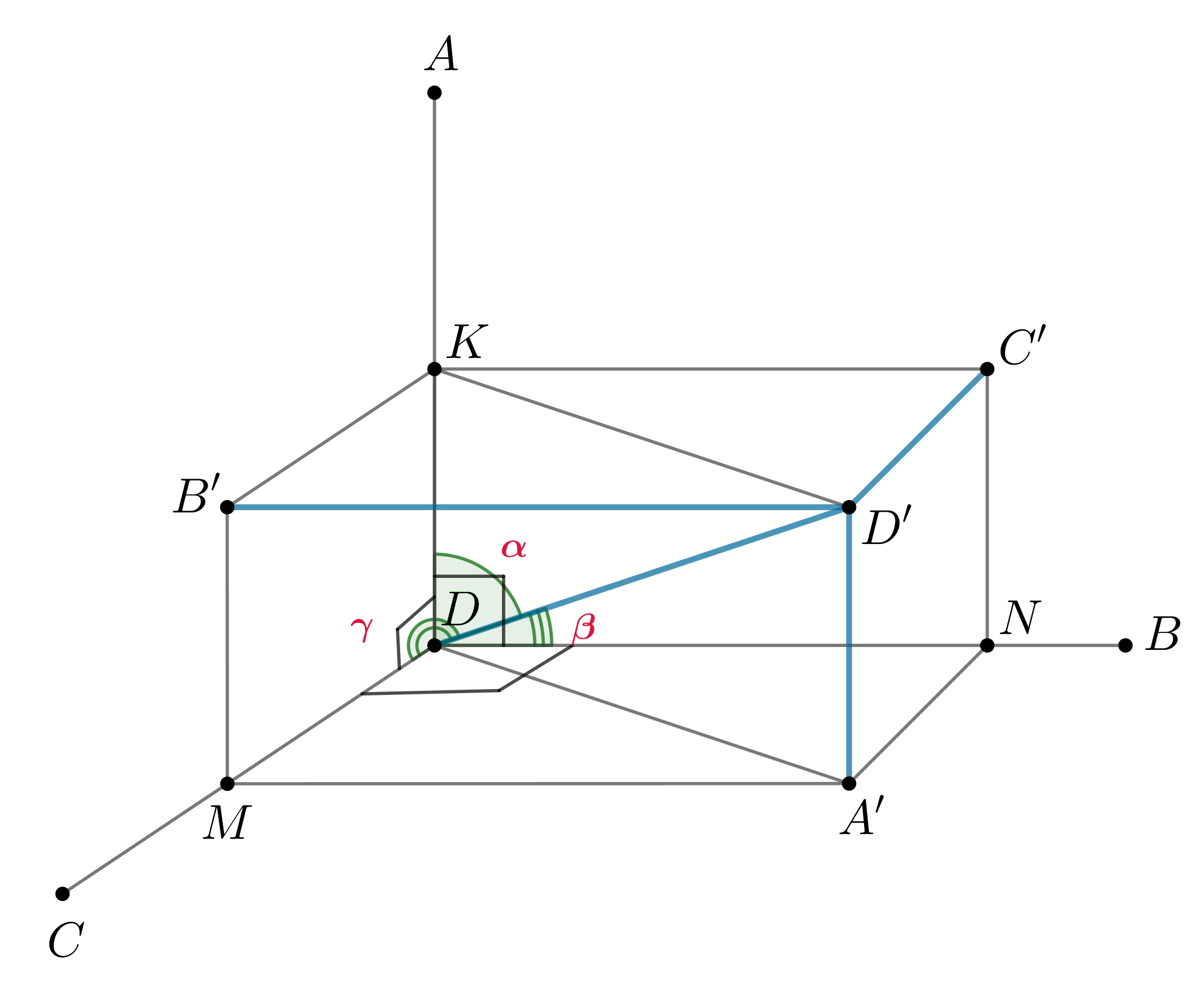
Тогда
Ошибка.
Попробуйте повторить позже
В тетраэдре плоские углы при вершине
прямые. Углы между гранями
,
и
и основанием
равны
и
соответственно. Докажите, что
Пусть ,
,
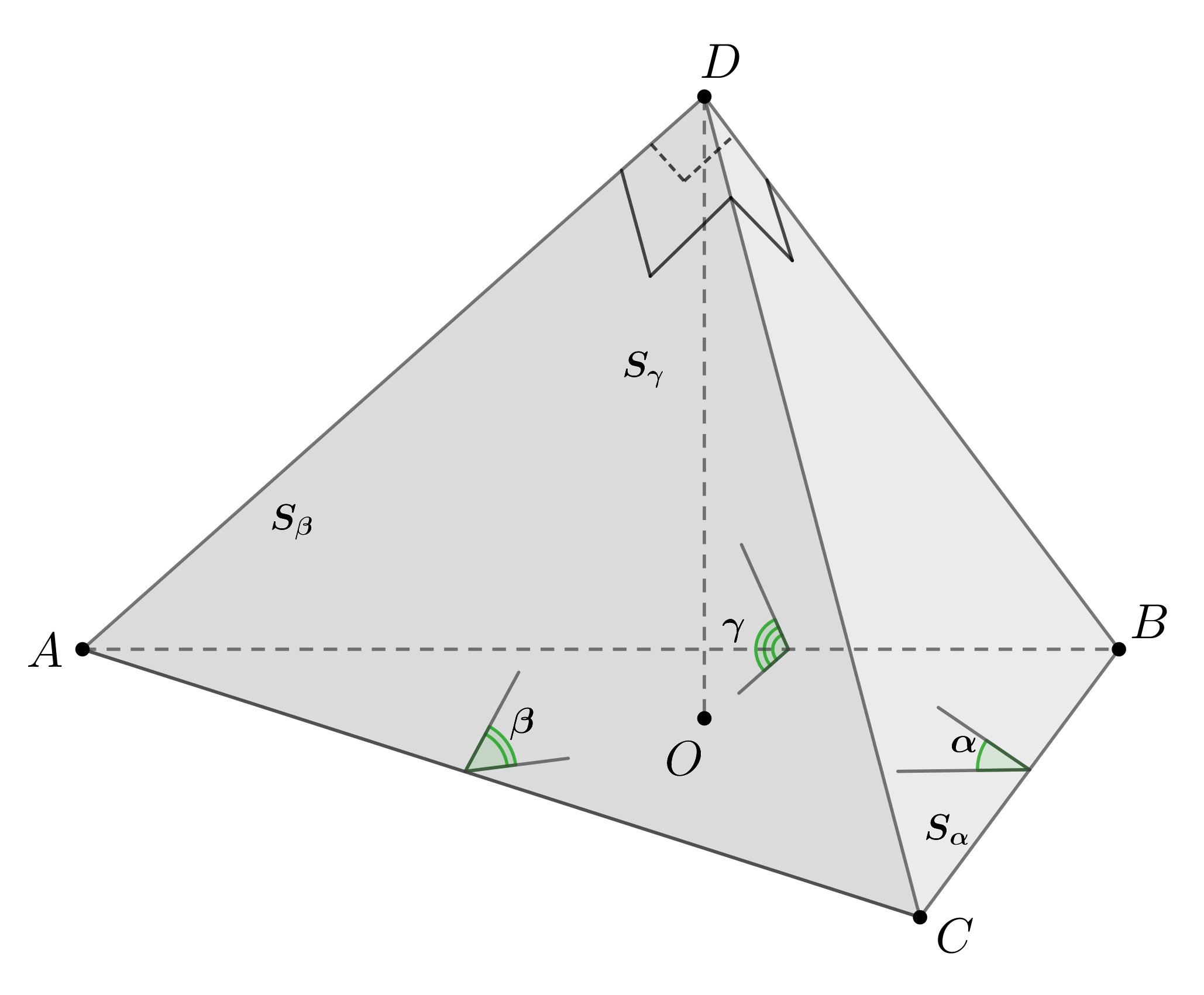
Проведем высоту Будем пользоваться теоремой “площадь проекции многоугольника на некоторую плоскость равна
произведению площади того многоугольника на косинус угла между плоскостью многоугольника и плоскостью проекции этого
многоугольника”.
Тогда для и его проекции
на плоскость
получаем:
. Аналогично
,
Так как все плоские углы при прямые, то
,
,
. Следовательно, для
и его
проекции
получаем
. Аналогично
,
.
Так как
то подставляя в это равенство ,
,
, получим:
Ошибка.
Попробуйте повторить позже
В тетраэдре плоские углы при вершине
прямые. Докажите, что сумма квадратов площадей трех его граней равна квадрату
площади оставшейся грани:
(пространственная теорема Пифагора)
По задаче id34258 следует, что, если ,
,
, углы между гранями
,
и
и
основанием
равны
и
соответственно, то
где ,
,
.
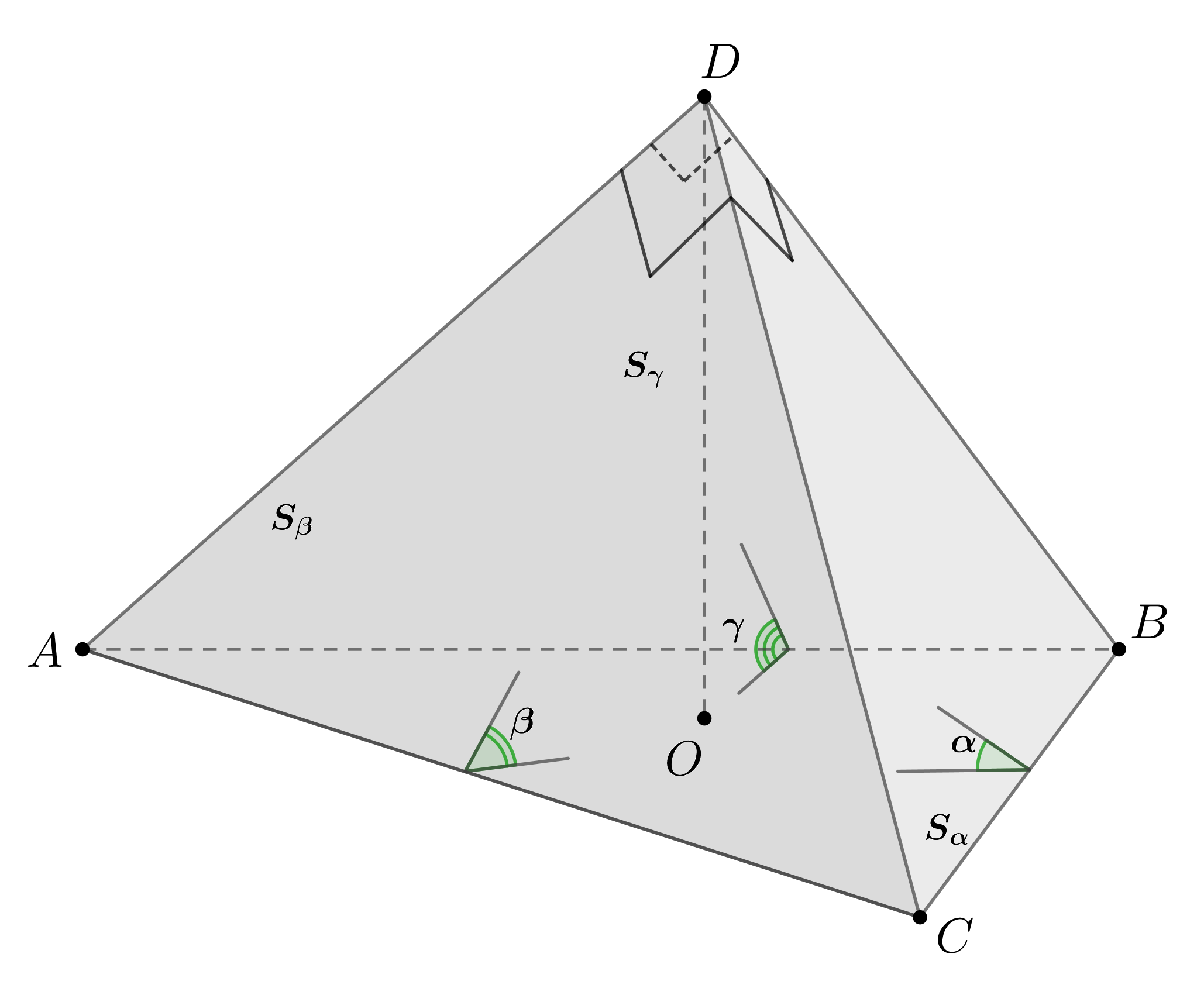
Выражая из последних равенств косинусы и подставляя в , получим
Ошибка.
Попробуйте повторить позже
Найдите (и докажите, почему это оно) геометрическое место точек, равноудаленных от некоторой плоскости.
Лемма 1
Плоскости и
параллельны. Тогда для всех точек плоскости
расстояния до плоскости
равны.
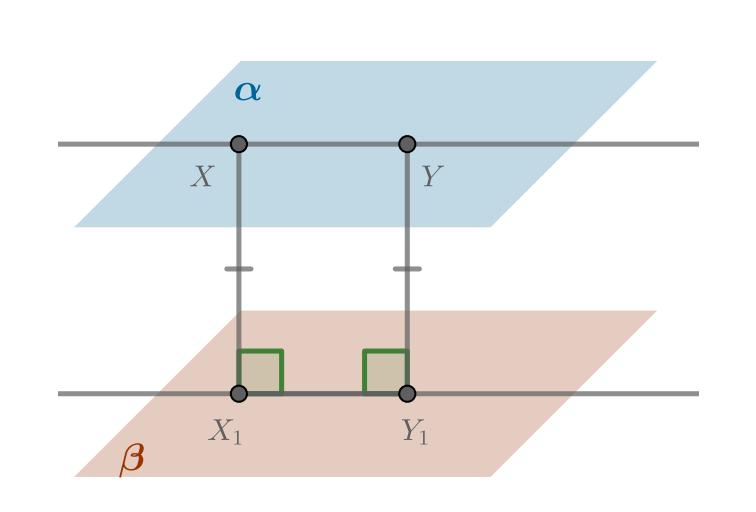
Доказательство
Возьмем две произвольные точки и докажем, что расстояние от
до
равно расстоянию от
до
. Расстояние от точки до плоскости по определению равно длине перпендикуляра из этой точки на эту плоскость.
Опустим перпендикуляры
и
на плоскость
. Прямые
и
лежат в одной плоскости, так как обе
перпендикулярны плоскости
. Прямые
и
также лежат в этой плоскости, т.е. они параллельны,
либо пересекаются. Если бы они пересекались в некоторой точке
, то эта точка принадлежала бы одновременно
плоскостям
и
, что противоречит
. Значит,
, и тогда из курса планиметрии мы знаем, что
.
Решение
Докажем, что от плоскости на расстояние
удалены те и только те точки, которые принадлежат двум
плоскостям
и
, параллельным
и удаленным от
на
. По Лемме 1 очевидно, что все точки таких двух
плоскостей действительно будут на расстоянии
от
.
![]()
Любая же точка, не принадлежащая этим плоскостям, будет удалена от на расстояние, меньшее
,
если она находится в части пространства между
и
, и на расстояние, большее
, в противном
случае.
Ошибка.
Попробуйте повторить позже
Найдите геометрическое место середин отрезков , где
— фиксированная точка вне плоскости
,
—
произвольная точка плоскости
.
Пусть — основание перпендикуляра из
на
,
— середина
. Тогда для любых точек
и
таких, что
,
— середина
, выполняется
как средняя линия. Исходя из этого
логично предположить, что искомое ГМТ — плоскость
, проходящая через
и параллельная
.
![]()
Докажем, что любая точка принадлежит ГМТ.
![]()
Пусть .
(т.к.
), причем
— середина
. Тогда
является серединой
,
а значит,
действительно принадлежит ГМТ.
Докажем теперь, что никакая точка не принадлежит ГМТ.
![]()
Пусть ,
(если одно из эти пересечений является пустым, то
точно не принадлежит
ГМТ). Если
, то
очевидно не принадлежит ГМТ. Тогда, аналогично вышеописанной ситуации,
—
середина
, но
. Таким образом,
не принадлежит ГМТ.
Ошибка.
Попробуйте повторить позже
Прямая перпендикулярна к плоскости треугольника
Докажите, что:
а) треугольник является проекцией треугольника
на плоскость
б) если — высота треугольника
, то
— высота треугольника
а) является проекцией точки
на плоскость
, а
и
проекциями отрезков
и
соответственно.
сам лежит в плоскости
. Значит,
— проекция
на плоскость
.
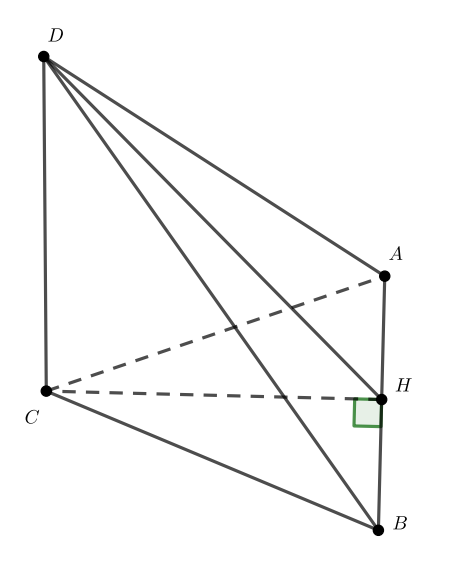
б) Проведем высоту в треугольнике
.
является проекцией
на плоскость
.
— высота, значит, прямая
перпендикулярна проекции
, следовательно, по теореме о трех
перпендикулярах перпендикулярна и наклонной
. Получили, что
, следовательно,
— высота в
.
Ошибка.
Попробуйте повторить позже
Докажите, что прямая , проведенная в плоскости
через основание
наклонной
перпендикулярно к ней,
перпендикулярна к ее проекции
.
![]()
Проведем в плоскости через точку
прямую
, перпендикулярную проекции
. Тогда по теореме о трех
перпендикулярах
. По условию
, мы показали, что
, тогда
. Тогда прямые
и
параллельны и обе проходят через точку
. Следовательно,
и
. Мы только что доказали теорему,
обратную теореме о трех перпендикулярах.
Ошибка.
Попробуйте повторить позже
Прямая перпендикулярна к плоскости прямоугольника
Докажите, что прямая, по которой
пересекаются плоскости
и
, перпендикулярна к плоскости
![]()
Рассмотрим плоскости ,
и
. Они попарно пересекаются, следовательно, прямые их пересечения
либо попарно параллельны, либо пересекаются в одной точке. Однако две из этих трех прямых пересечения это прямые
и
, которые параллельны, т.к.
— прямоугольникю Таким образом, вторая альтернатива (все три
прямые пересекаются в одной точке) заведомо невозможна. Тогда прямая
пересечения плоскостей
и
параллельная прямой
.
, а также
как стороны прямоугольника. Получили, что прямая
перпендикулярна двум прямым плоскости
, а значит, и самой плоскости. Тогда и прямая
, параллельная
, перпендикулярна плоскости
, что и требовалось доказать.
Ошибка.
Попробуйте повторить позже
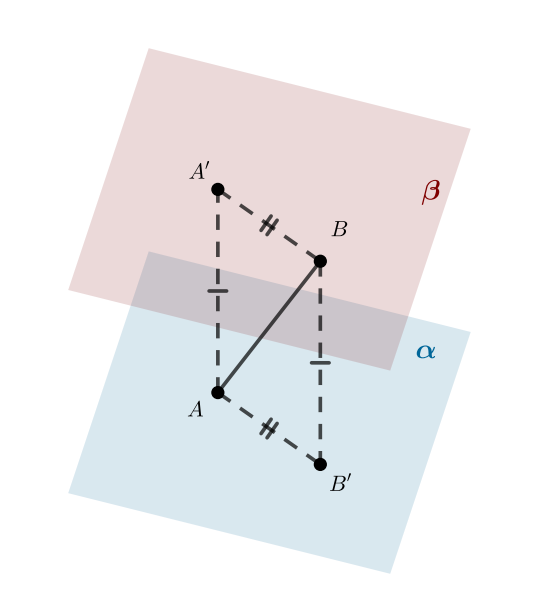
Концы отрезка лежат на двух параллельных плоскостях, расстояние между которыми равно
, причем
Докажите, что проекции отрезка
на эти плоскости равны. Найдите эти проекции, если
см,
см.
Пусть — проекция точки
на
,
— проекция точки
на
.
по определению проекции,
,
следовательно,
. Аналогично
и
. Тогда
и однозначно задают плоскость. Из
вышесказанного следует, что все углы четырехугольника
прямые, он является прямоугольником. В
прямоугольнике противолежащие стороны равны, т.е.
, что и требовалось доказать (проекции
равны).
По теореме Пифагора длина этих проекций равна .
12
Ошибка.
Попробуйте повторить позже
Луч не лежит в плоскости неразвернутого угла
Докажите, что если
, причем
, то проекцией луча
на плоскость
является биссектриса угла
.
Опустим перпендикуляры на
и
на
. Из прямоугольного треугольника
имеем
. Из прямоугольного треугольника
имеем
.
Воспользовавшись равенством углов из условия, получаем
.
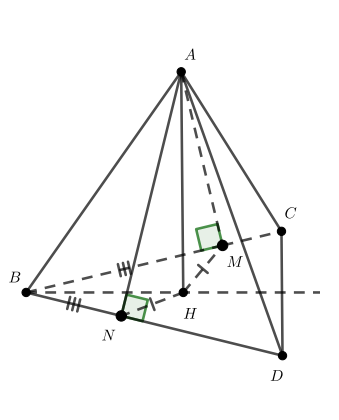
Опустим перпендикуляр на
, тогда луч
— проекция луча
на эту плоскость.
Проведем
и
. Прямая
перпендикулярна наклонной
, следовательно, по обратной
теореме о трех перпендикулярах (№5) перпендикулярна и ее проекции, т.е.
. Аналогично
.
Прямоугольные треугольники и
равны по гипотенузе (
— общая) и катету
,
следовательно, их оставшиеся катеты тоже равны
.
Имеем ,
,
, т.е. точка
равноудалена от сторон угла
, следовательно,
— биссектриса угла
.



