01 Графический метод решения
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
В какой координатной четверти пересекаются графики уравнений и
Источники:
Эту задачу можно решить как алгебраически, так и графически.
Первое решение.
Начнём с алгебраического решения. Решим систему:
Решение системы — Значит, данные нам прямые пересекаются в точке
прямые пересекаются в
координатной четверти.
Второе решение.
Чтобы решить эту задачу графически, необходимо изобразить прямые и
и посмотреть, в какой координатной
четверти они пересекутся:
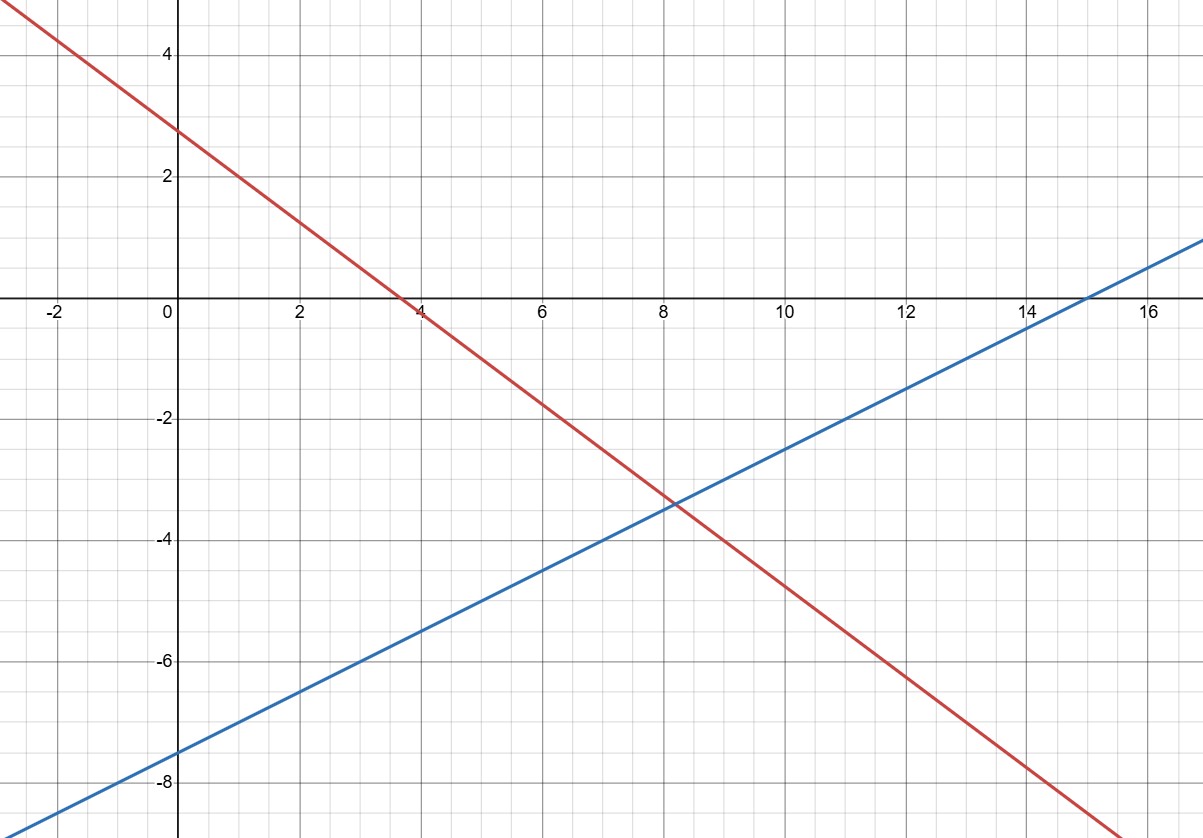
Видно, что прямые пересекаются в координатной четверти.
В координатной четверти.
Ошибка.
Попробуйте повторить позже
(a) Если графики и
пересекаются на оси абсцисс, то
То есть наши уравнения выглядят, как
и
Тогда
Также мы могли бы решить эту задачу графически: — прямая, проходящая через точки
и
А
—
множество прямых, параллельных прямой
Чтобы выяснить, при каком значении
графики наших уравнений пересекаются на
оси абсцисс, мы могли перемещать линейку параллельно прямой
пока прямые
и
не пересекутся на оси
абсцисс, а потом найти значение параметра
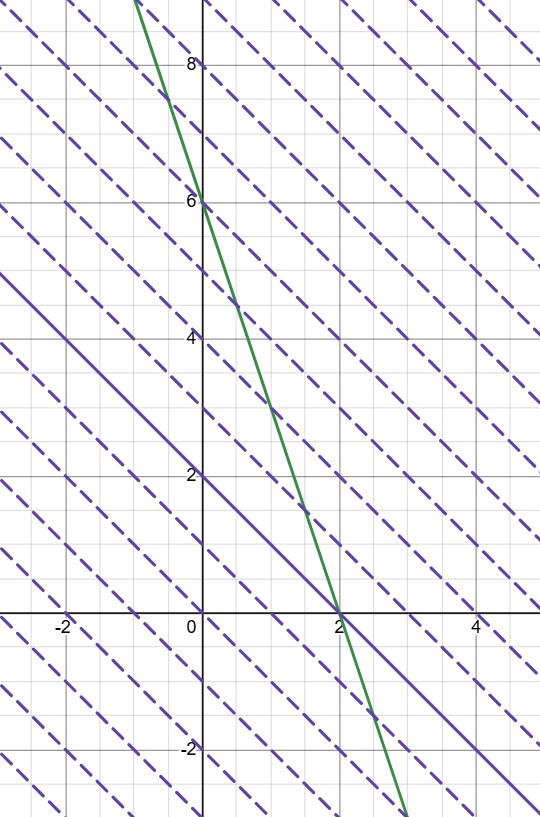
(b) Если графики и
пересекаются на оси ординат, то
То есть наши уравнения выглядят, как
и
Тогда
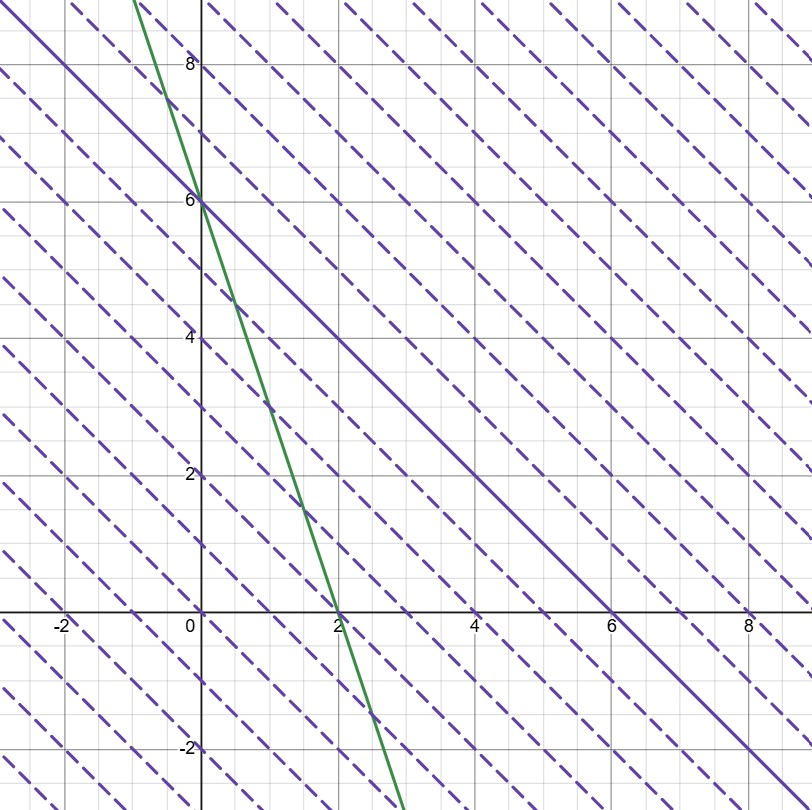
Также мы могли бы решить эту задачу графически: — прямая, проходящая через точки
и
А
—
множество прямых, параллельных прямой
Чтобы выяснить, при каком значении
графики наших уравнений пересекаются на
оси ординат, мы могли перемещать линейку параллельно прямой
пока прямые
и
не пересекутся на оси
ординат, а потом найти значение параметра
Ошибка.
Попробуйте повторить позже
При каком значении графики уравнений
пересекаются в одной точке?
Источники:
Эту задачу можно решить как алгебраически, так и графически.
Первое решение.
Начнём с алгебраического решения. Выясним, где пересекаются графики первых двух уравнений, решив систему:
Графики первых двух уравнений пересекаются в точке График уравнения
также должен проходить через эту
точку. Значит, если мы подставим вместо
абсциссу этой точки, а вместо
— ординату, то мы должны получить верное
равенство:
Второе решение.
Теперь решим эту задачу графически. — прямая, проходящая через точки
и
— прямая,
проходящая через точки
и
— прямая, проходящая через точку
Изобразим графики первых двух
уравнений и начнём вращать линейку около точки
до тех пор, пока она не будет проходить через точку пересечения первых двух
прямых, а потом найдём значение параметра
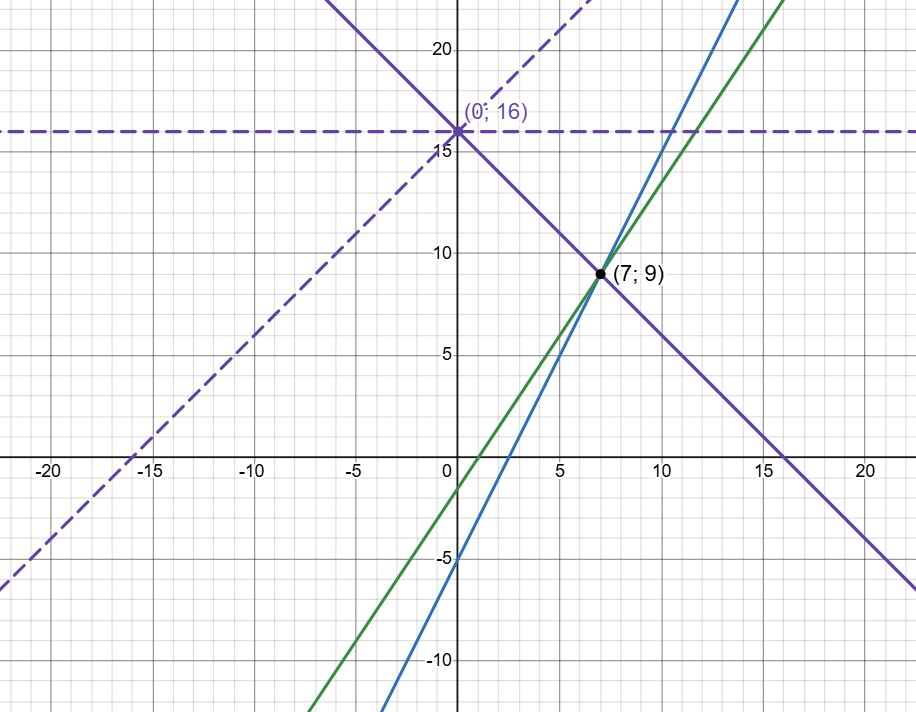
Ошибка.
Попробуйте повторить позже
График — множество прямых, проходящих через точку
(a) График — прямая, проходящая через точки
и
Изобразим график этого уравнения и начнём вращать
линейку около точки
до тех пор, пока
и
не будут параллельны, а потом найдём значение параметра
Таким образом,
(b) График — прямая, проходящая через точки
и
Прямые
и
никогда не
будут параллельны, т. к. обе проходят через точку
т. е. или пересекаются, или совпадают. Получается, таких
не
существует.
Ошибка.
Попробуйте повторить позже
Напишите уравнение прямой, проходящей через точку и через точку пересечения графиков функций
и
Источники:
Для начала найдём точку пересечения графиков функций и
Это можно сделать как алгебраически, так и
графически.
Начнём с алгебраического способа. Чтобы найти точку пересечения этих функций, решим систему:
Таким образом, графики функций и
пересекаются в точке
Также, чтобы найти точку пересечения этих двух функций, мы могли нарисовать графики функций и
и посмотреть,
где они пересекутся.
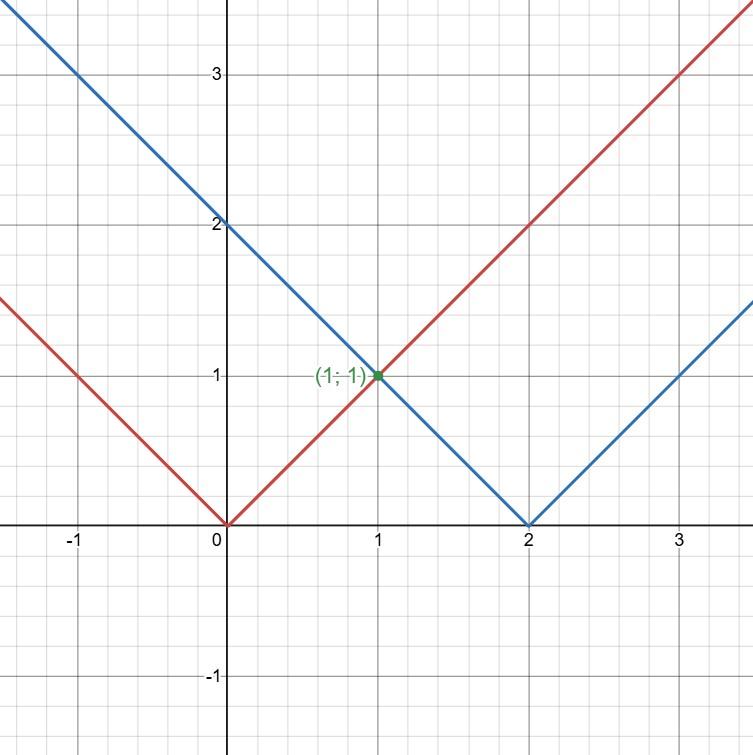
Видно, что “галочки” пересекаются в
Теперь нам необходимо написать уравнение прямой, проходящей через точки и
Это, опять же, можно сделать
алгебраически и графически.
Временно запишем уравнение нашей прямой, как Оно должно проходить через точки
и
значит, если мы
поочерёдно подставим в уравнение координаты каждой из этих точек, равенство должно быть верным. Тогда имеет смысл следующая
система:
Таким образом, наше уравнение выглядит, как то есть как
Также мы могли найти коэффициенты этого уравнения графически. Для этого мы должны были изобразить точки и
нарисовать прямую, проходящую через них, и найти её уравнение:
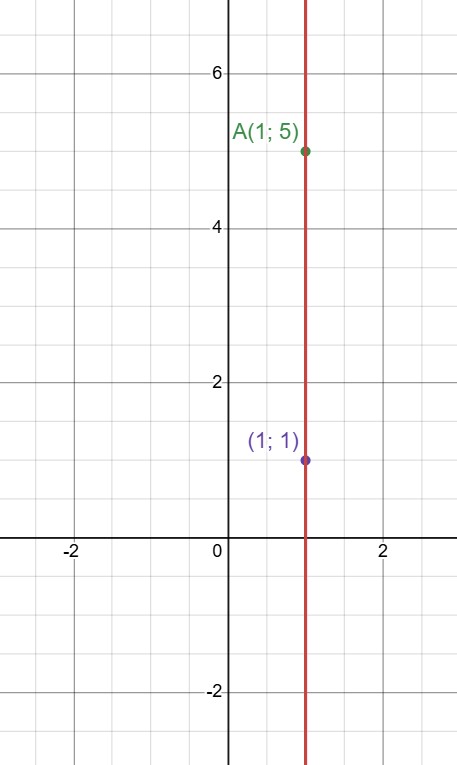
Ошибка.
Попробуйте повторить позже
(a) Выясним, как будут выглядеть графики уравнений системы и изобразим их:
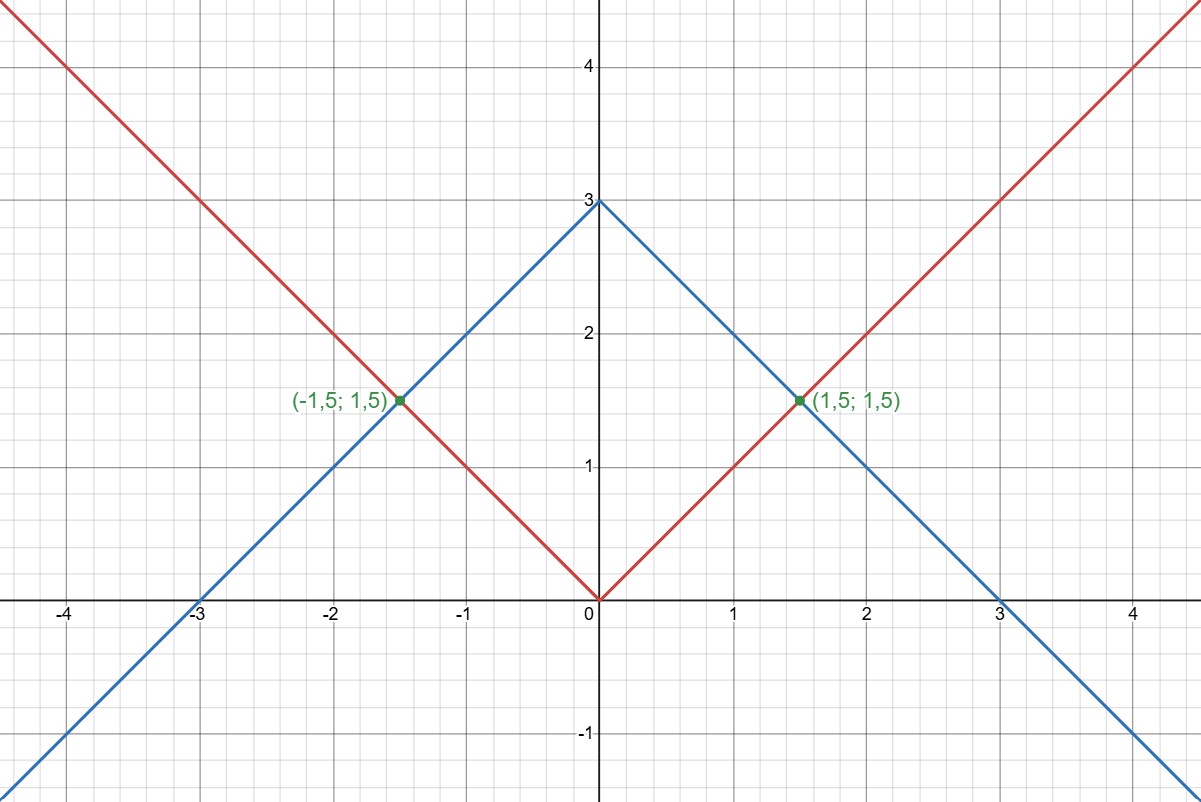
(b) Выясним, как будут выглядеть графики уравнений системы и изобразим их:
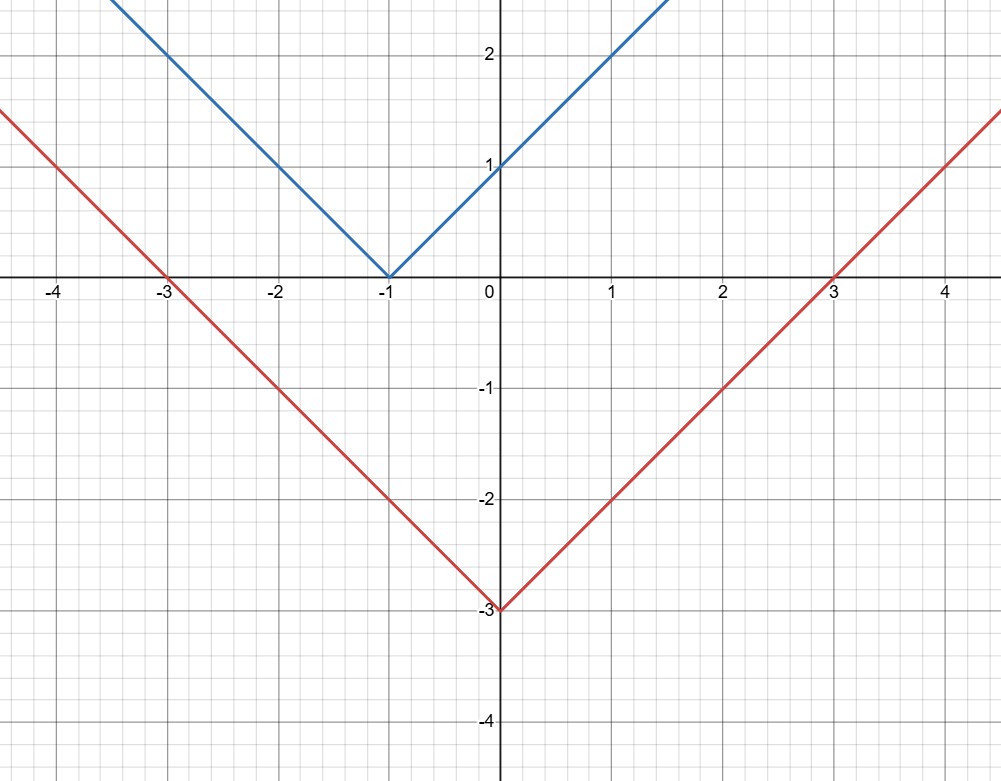
(c) Выясним, как будут выглядеть графики уравнений системы и изобразим их:
(d) Выясним, как будут выглядеть графики уравнений системы и изобразим их:
При “галочки” будут иметь ровно
точку пересечения: левая ветвь “галочки”
пересекает правую ветвь
“галочки”
При “галочки” будут совпадать.
При “галочки” будут иметь ровно
точку пересечения: правая ветвь “галочки”
пересекает левую ветвь
“галочки”
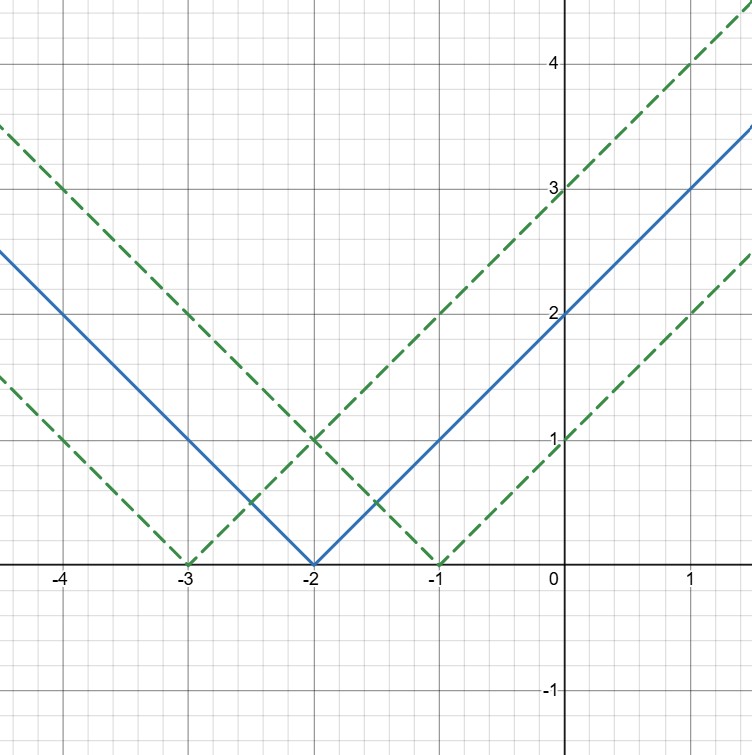
Ошибка.
Попробуйте повторить позже
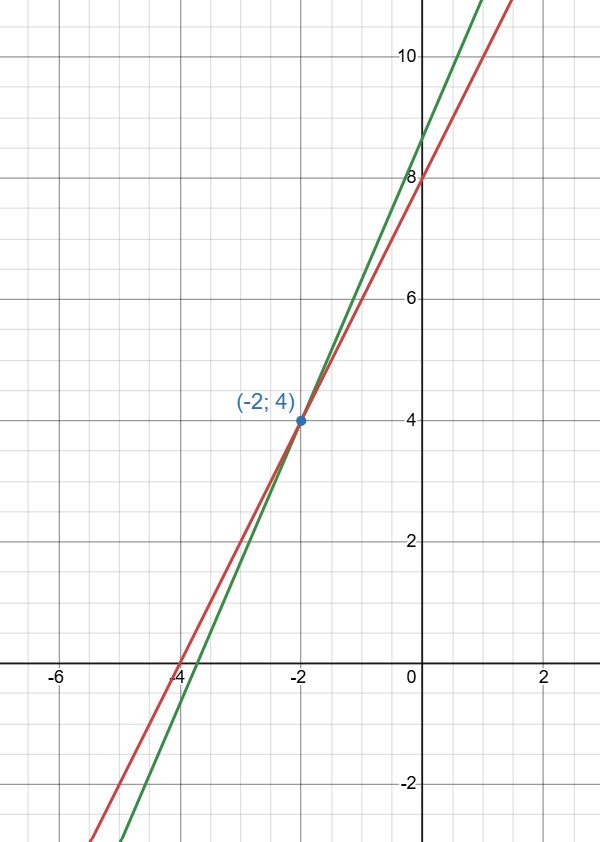
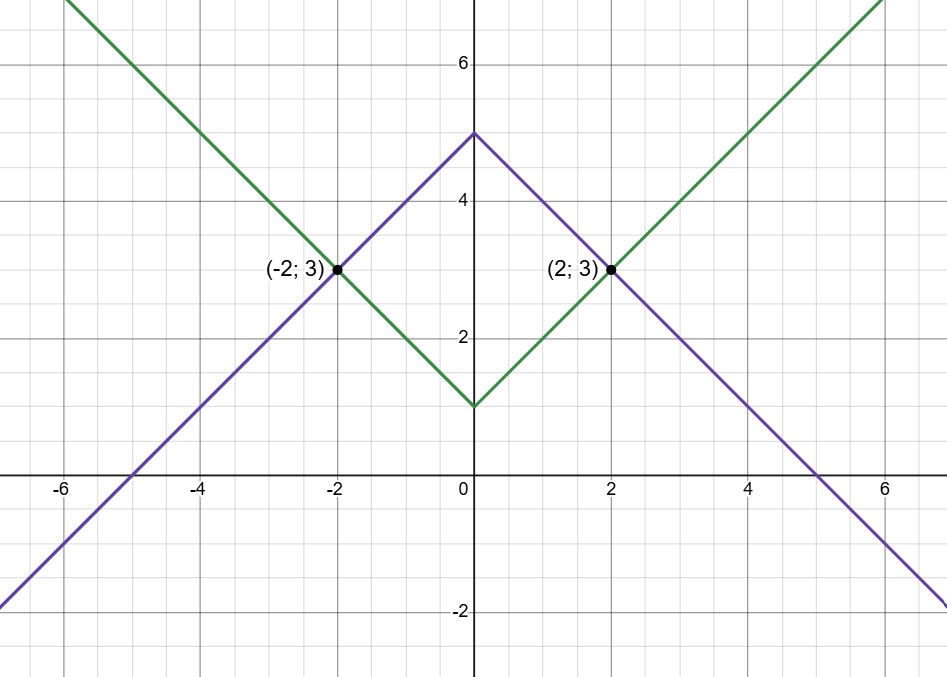
(b) Разберёмся, что за график имеет первое уравнение в системе, и изобразим графики:
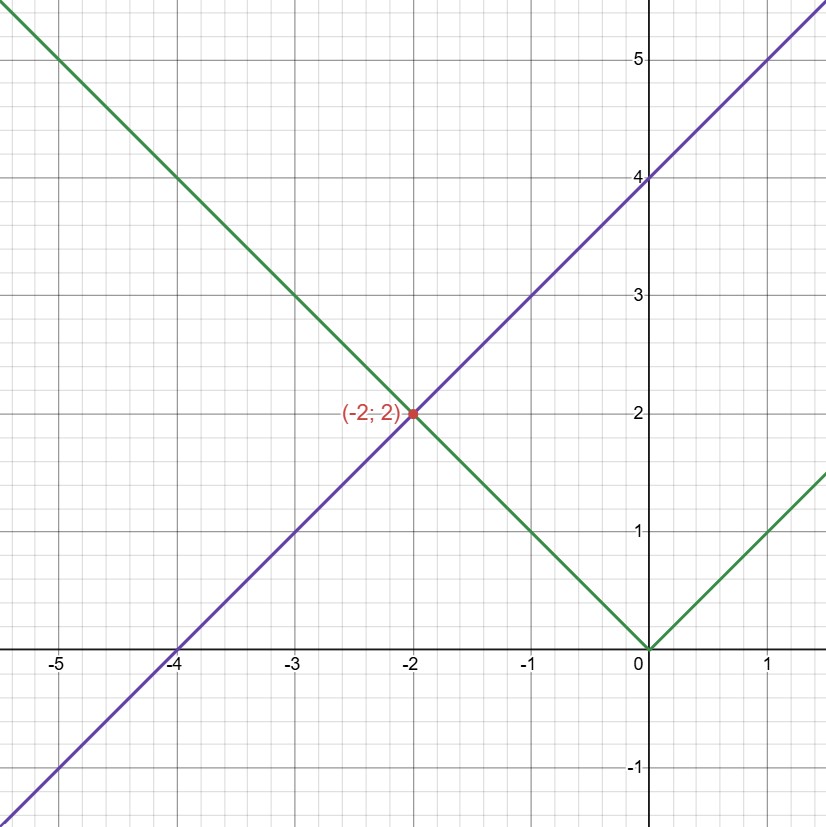
(c) Разберёмся, что за график имеет первое уравнение в системе, и изобразим графики:
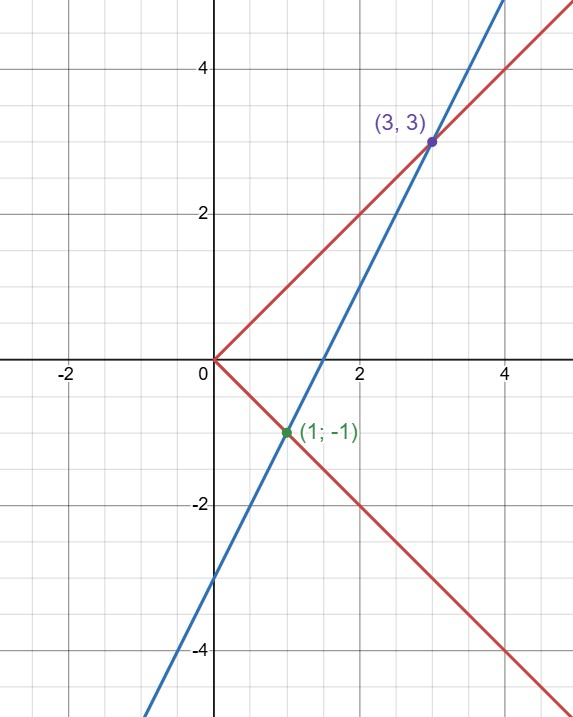
(d) Разберёмся, что за график имеет первое уравнение в системе, и изобразим графики:
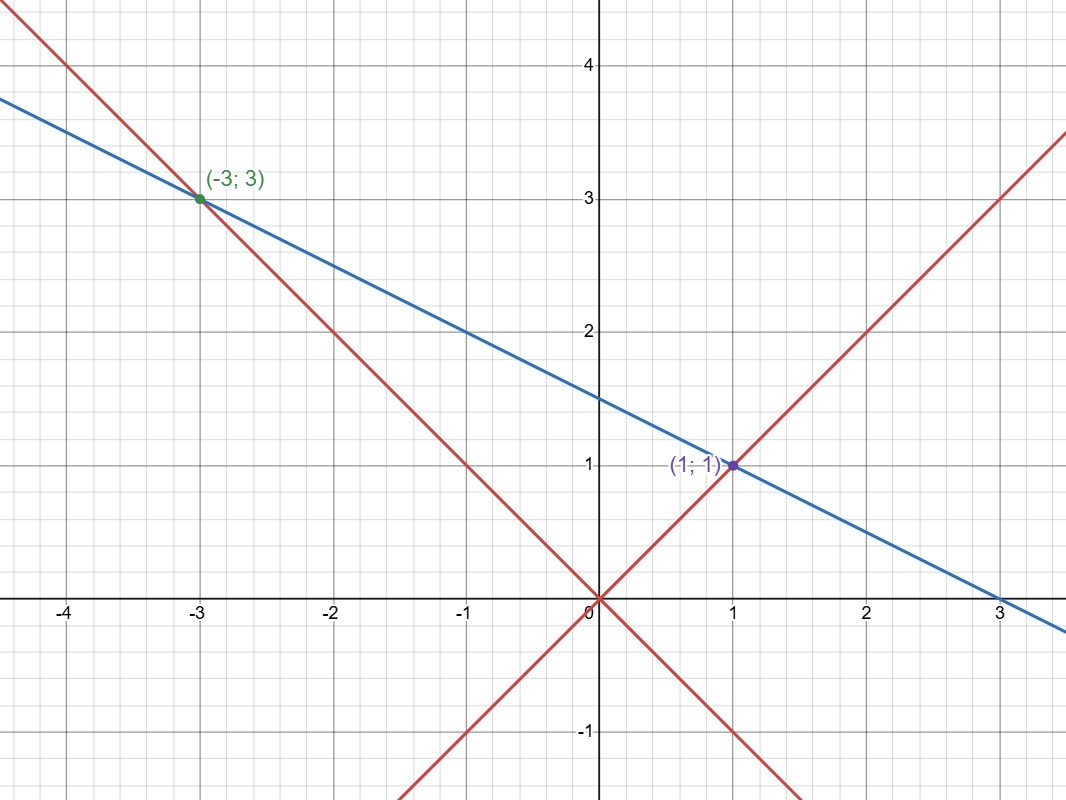
(e) Разберёмся, что за график имеет первое уравнение в системе, и изобразим графики:
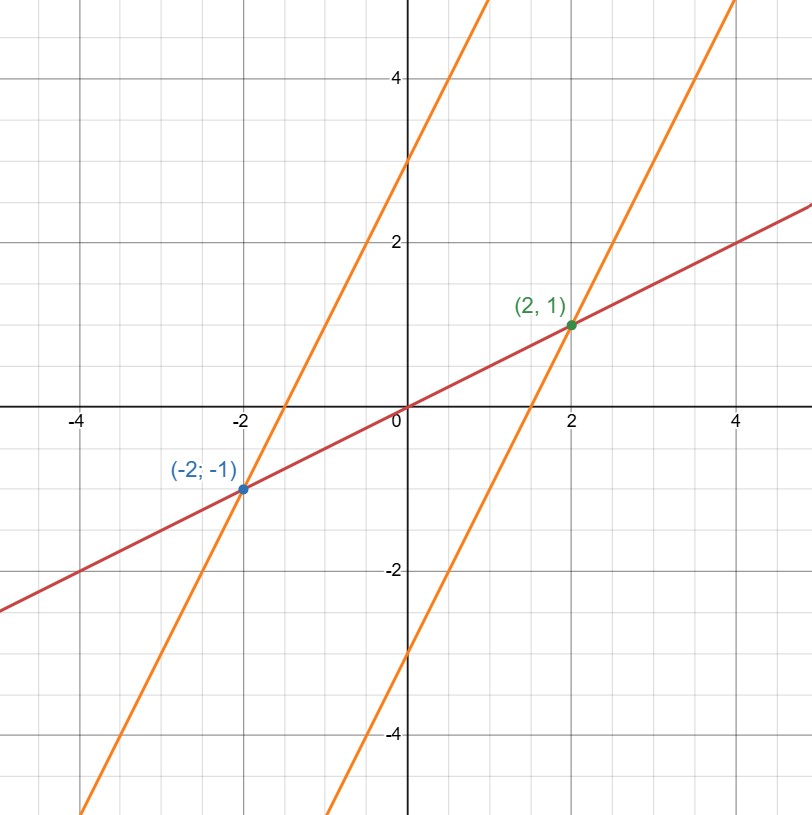
(f) Выясним, как будут выглядеть графики уравнений системы и изобразим их:
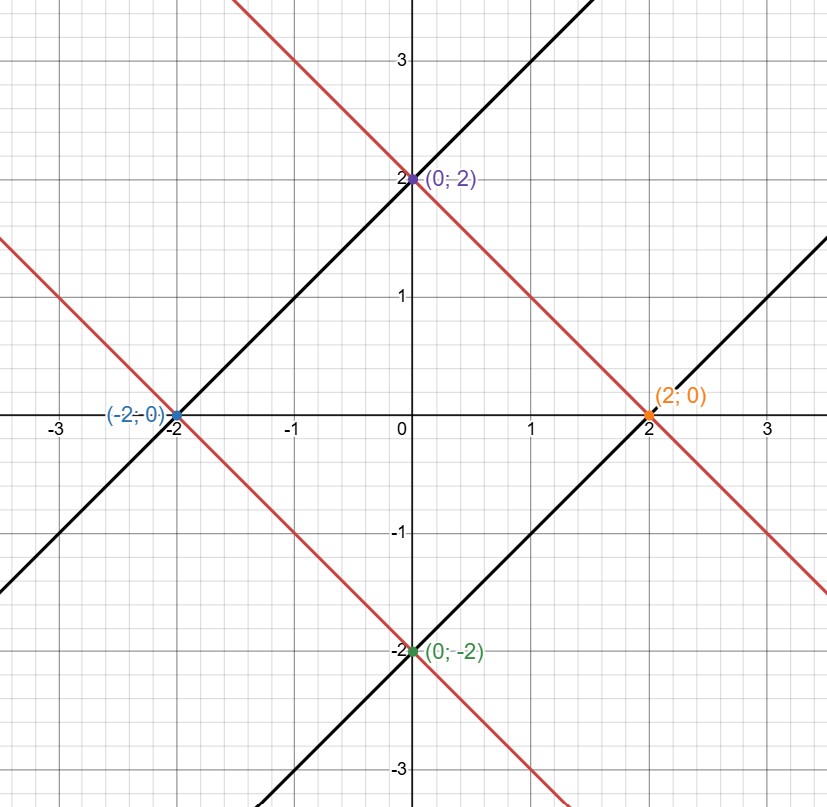
(g) Выясним, как будут выглядеть графики уравнений системы и изобразим их:
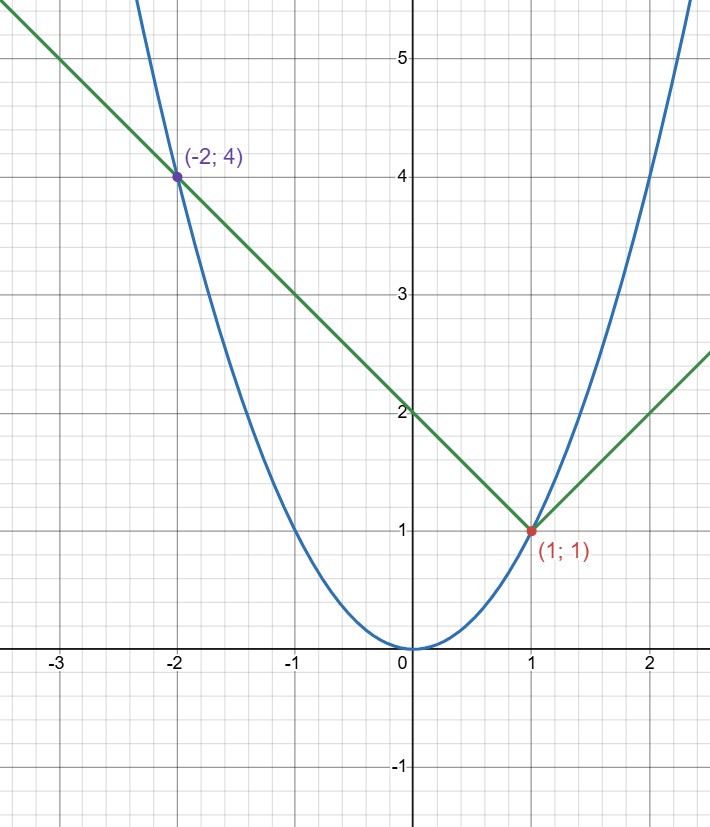
(h) Выясним, как будут выглядеть графики уравнений системы и изобразим их:
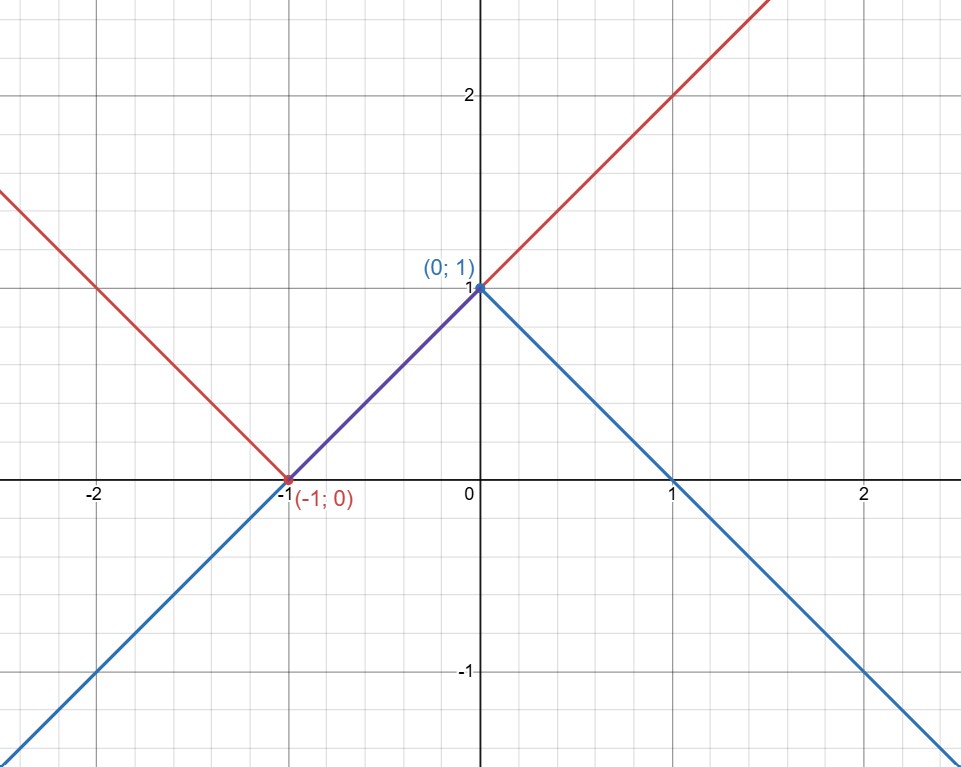
Ошибка.
Попробуйте повторить позже
Решите систему уравнений:
Источники:
Первое решение.
Вычтем из
Подставим в
Получается,
Второе решение.
Изобразим графики обоих уравнений и найдём точку их пересечения.
— прямая, пересекающая ось абсцисс в
ось ординат — в
— прямая, пересекающая ось абсцисс в
ось ординат — в
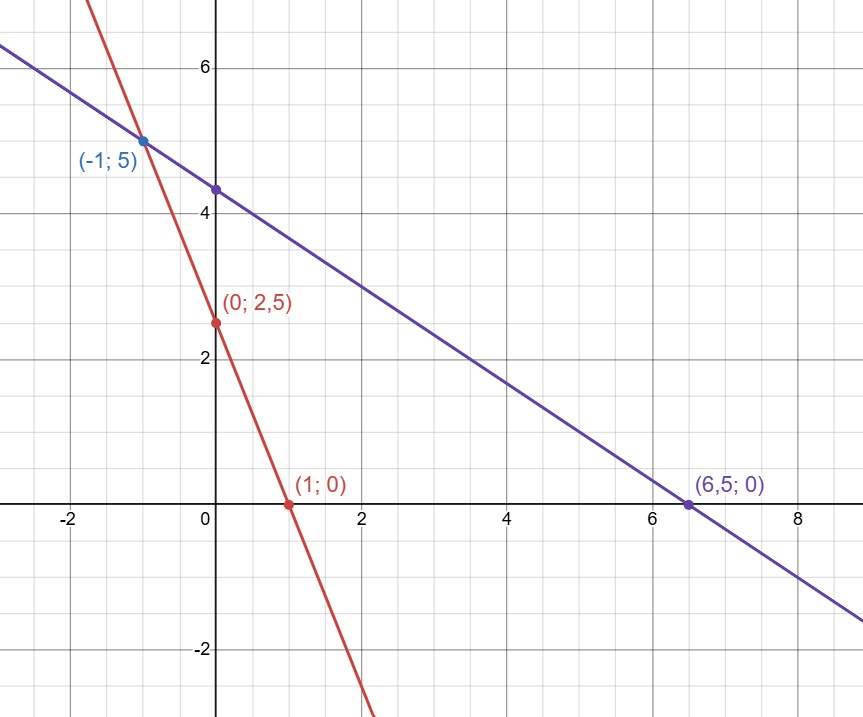
Получается,
Ошибка.
Попробуйте повторить позже
Выясните, сколько решений имеет система уравнений:
Источники:
Первое решение.
Вычтем из
Подставим в
Получается, уравнение имеет единственное решение —
Второе решение.
Изобразим графики уравнений и выясним, сколько у них точек пересечения.
— прямая, пересекающая ось абсцисс в
ось ординат — в
— прямая, пересекающая ось абсцисс в
ось ординат — в
Уже видно, что система будет иметь единственное решение потому что обе прямые проходят через эту точку и не могут
пересекаться в двух и более точках. Но для наглядности убедимся в этом, изобразив прямые:
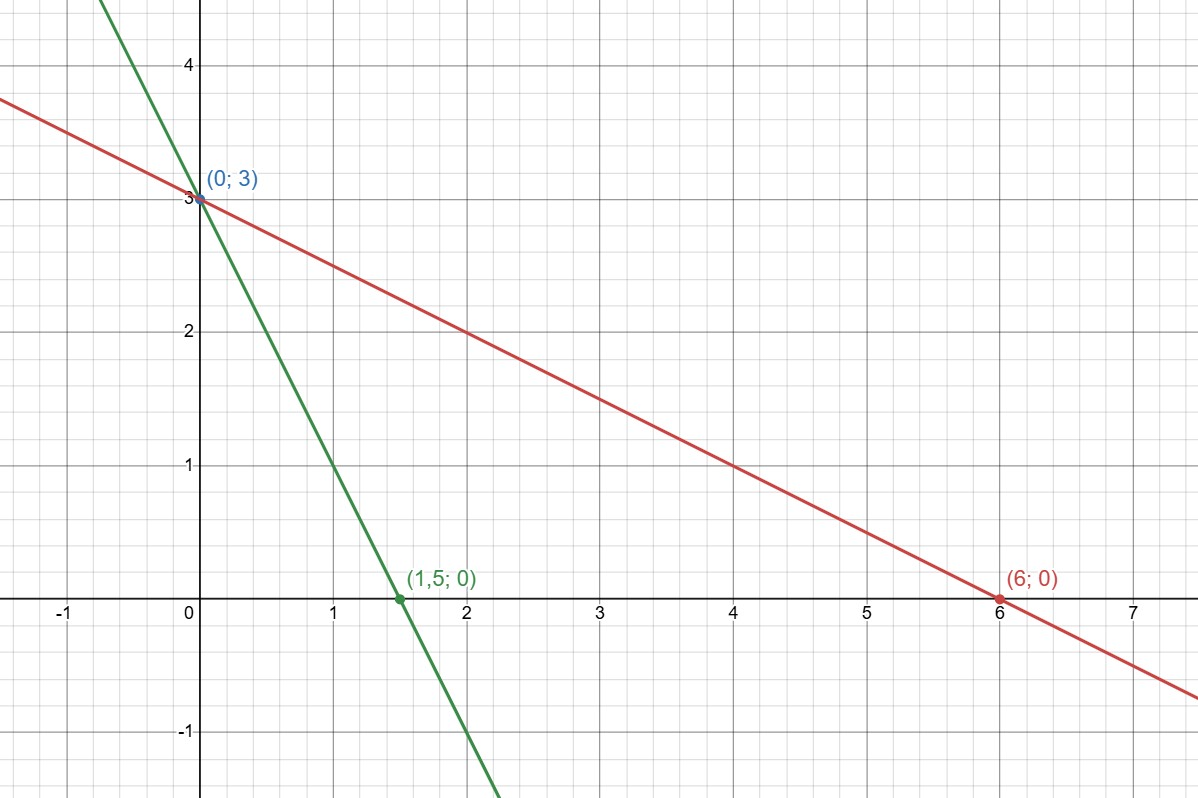
Получается, уравнение имеет единственное решение —
Ошибка.
Попробуйте повторить позже
Выясните, сколько решений имеет система уравнений:
Источники:
Первое решение.
Система не имеет решений.
Второе решение.
Изобразим графики уравнений и выясним, сколько у них точек пересечения.
— прямая, пересекающая ось абсцисс в
ось ординат — в
— прямая, пересекающая ось абсцисс в
ось ординат — в
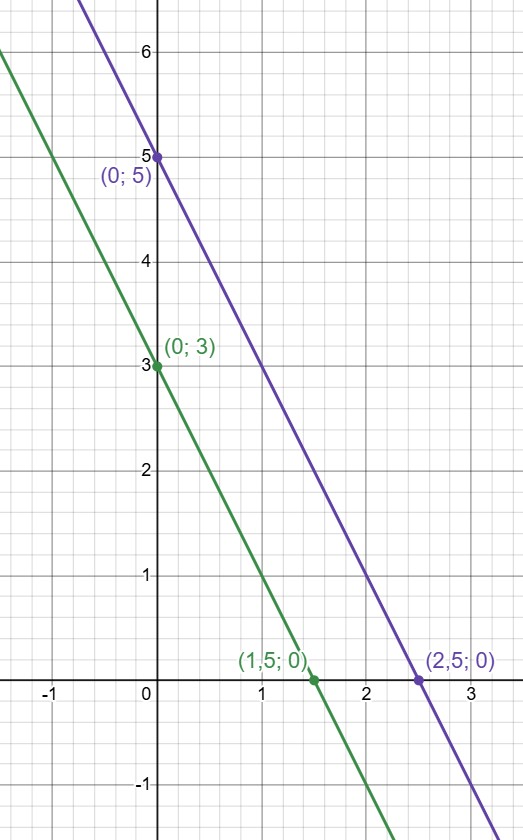
Прямые параллельны, система не имеет решений.
Ошибка.
Попробуйте повторить позже
Выясните, сколько решений имеет система уравнений:
Источники:
Первое решение.
Система имеет бесконечно много решений вида
Второе решение.
Изобразим графики уравнений и выясним, сколько у них точек пересечения.
— прямая, пересекающая ось абсцисс в точке
ось ординат — в точке
— прямая, пересекающая ось абсцисс в точке
ось ординат — в точке
Уже ясно, что прямые совпадут, т. к. две точки однозначно задают прямую. Но для наглядности убедимся в этом, изобразив прямые:
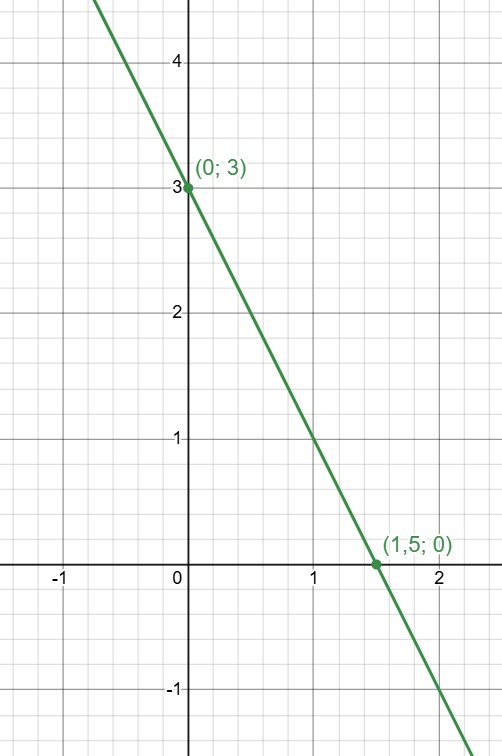
Прямые совпали. Системе удовлетворяют все точки, лежащие на получившейся прямой.
Бесконечно много решений вида
Ошибка.
Попробуйте повторить позже
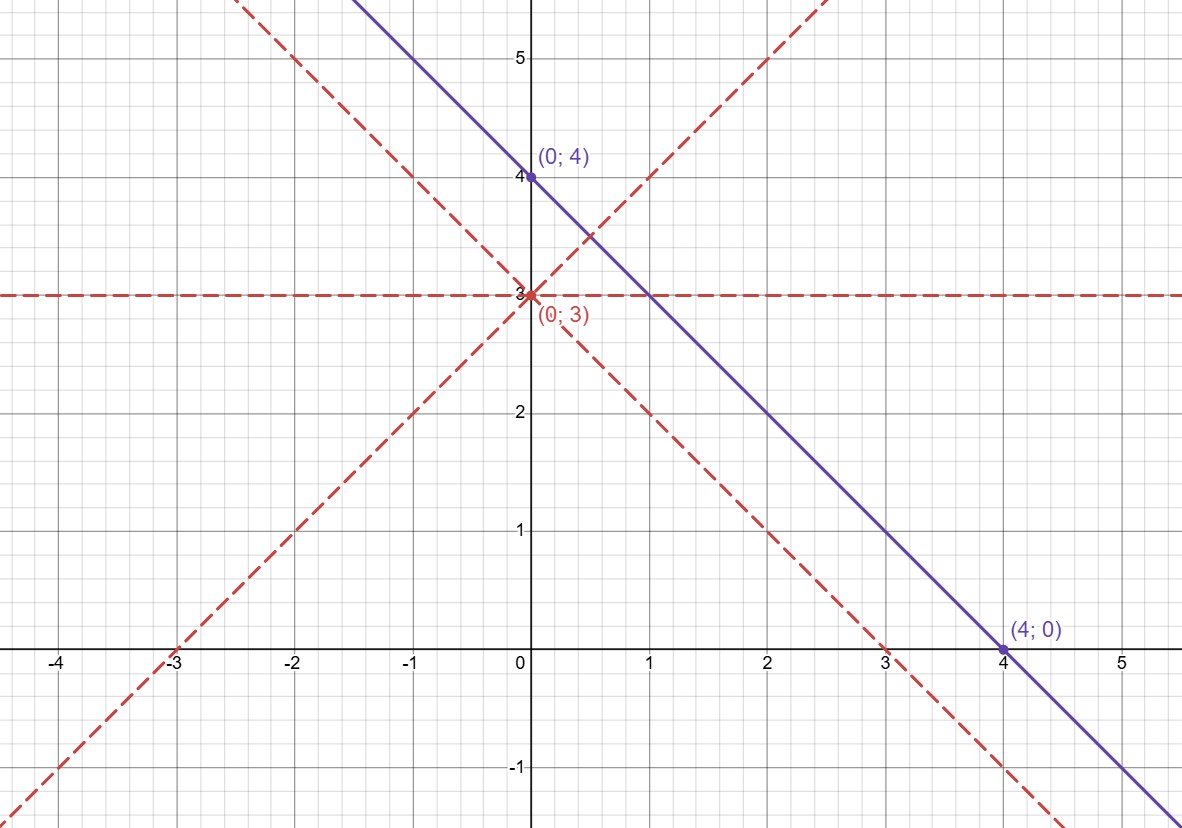
(a) Изобразим графики уравнений и выясним, где они пересекаются:
— прямая, пересекающая ось абсцисс в
ось ординат — в
— прямая, пересекающая ось абсцисс в
ось ординат — в
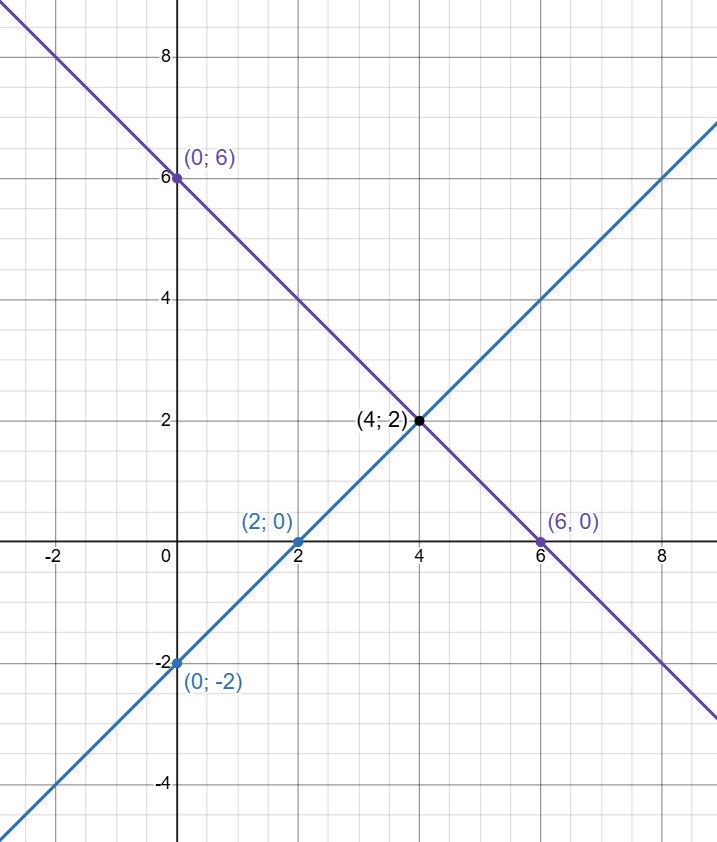
Уравнение имеет единственное решение
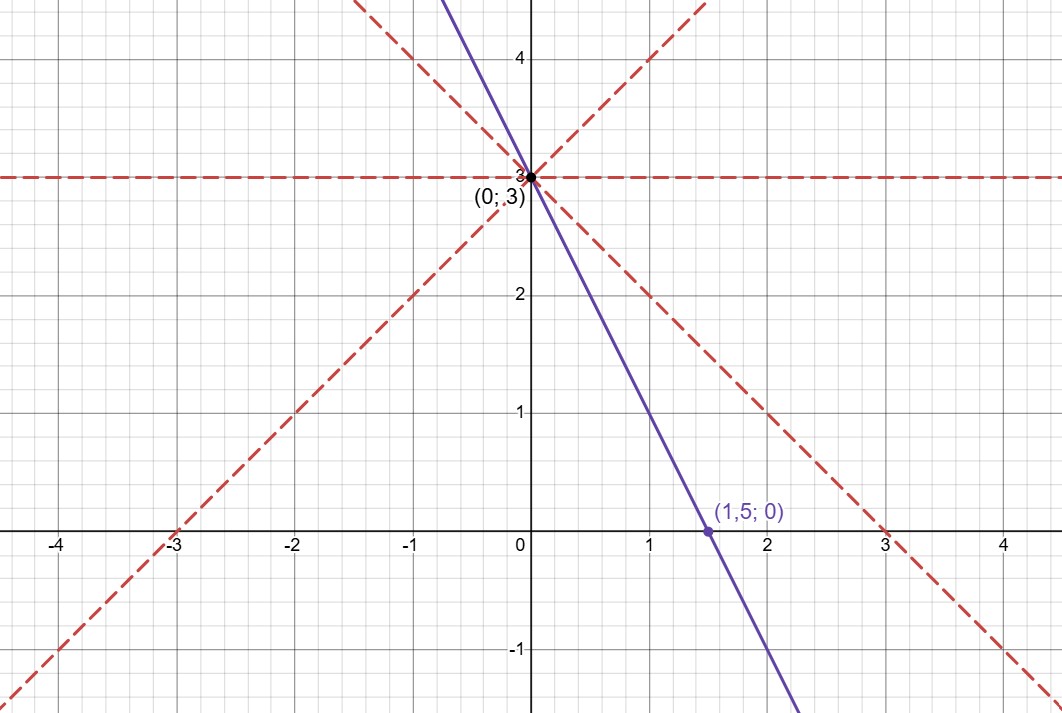
(b) Изобразим графики уравнений и выясним, где они пересекаются:
— прямая, пересекающая ось абсцисс в
ось ординат — в
— прямая, пересекающая ось абсцисс в
ось ординат — в
Уже ясно, что прямые совпадут, т. к. две точки однозначно задают прямую. Но для наглядности убедимся в этом, изобразив прямые:
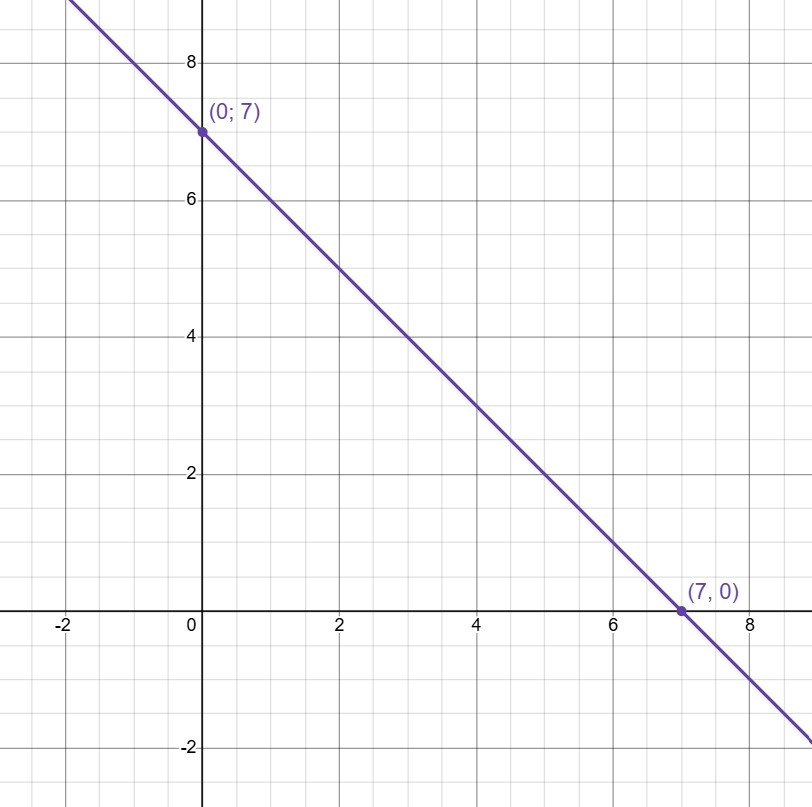
Прямые совпали. Системе удовлетворяют все точки, лежащие на получившейся прямой.
(c) Изобразим графики уравнений и выясним, где они пересекаются:
— прямая, пересекающая ось абсцисс в
ось ординат — в
— прямая, пересекающая ось абсцисс в
ось ординат —
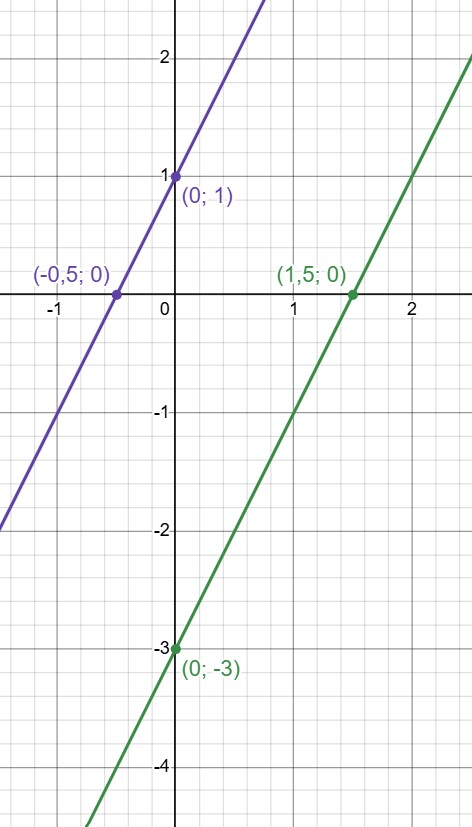
Прямые параллельны, система не имеет решений.



