Оценка + пример
Ошибка.
Попробуйте повторить позже
Во всех клетках таблицы записаны положительные числа. На некоторых
клетках отдыхают свиньи, заслоняя числа в этих
клетках. Костя посчитал сумму всех видимых чисел и получил
Потом каждая свинья перебралась в соседнюю по стороне клетку, и
Костя насчитал сумму
Потом свиньи снова перебрались, и у Кости получилась сумма
и т. д. — каждая новая
сумма оказывалась в
раз больше предыдущей. В одну клетку две свиньи не помещаются. Сколько раз такое могло
повторяться?
Оценка. На всех клетках, которые были видны вначале, стоят числа, не превосходящие Поскольку после первого перепрыгивания
сумма чисел сильно увеличилась, стали видны какие-то клетки, ранее заслоненные лягушками. Очевидно, числа, записанные на этих
клетках, не превосходят
После второго перепрыгивания сумма чисел опять сильно увеличилась, и это могло произойти лишь за счет
того, что стали видны еще какие-то клетки, которых не было видно ни в первый, ни во второй раз. При этом числа, стоящие на вновь
открывшихся клетках, заведомо не превосходят
Рассуждая таким образом, мы устанавливаем, что после каждого очередного перепрыгивания должны открыться клетки, которых до этого ни разу не было видно.
Поскольку вначале лягушки заслоняют всего клеток, количество перепрыгиваний, позволяющих сумме так сильно увеличиваться, не
может быть больше
Пример. Пусть лягушки занимают самые левые клеток нижней строки таблицы, и всякий раз каждая лягушка прыгает на соседнюю
справа клетку. Пусть на клетках, где стоят лягушки, написаны числа
а во всех остальных клетках таблицы написано число
Полагая
получаем требуемое
Пять раз
Ошибка.
Попробуйте повторить позже
Есть коробок, пронумерованных числами от
до
В одной коробке лежит приз, и ведущий знает, где он находится. Зритель
может послать ведущему пачку записок с вопросами, требующими ответа “да” или “нет”. Ведущий перемешивает записки в пачке и, не
оглашая вслух вопросов, честно отвечает на все. Какое наименьшее количество записок нужно послать, чтобы наверняка узнать, где
находится приз?
Чтобы можно было однозначно определить, в какой из коробок лежит приз, требуется возможность получить хотя бы
различных ответов на один набор вопросов. Так как ответы ведущего для различных положений приза могут отличаться
только числом “да” среди них, то требуется возможность получить в ответ хотя бы
различных количеств “да”. Значит,
требуется хотя бы
вопросов (от
до
“да”). Пример на
вопросов. Пусть
-ый вопрос: «Номер коробки, в
которой лежит приз, меньше либо равен
?». Тогда если ответов “да” ноль, то приз в сотой коробке, если один, то в
-й и
т.д.
Ошибка.
Попробуйте повторить позже
Король обошел шахматную доску, побывав на каждом поле по разу, и последним ходом вернулся на исходное поле. Ломаная, соединяющая последовательно центры полей в пути короля, не имеет самопересечений. Какую наибольшую длину она может иметь?
Король сделал хода. Поскольку длина каждого хода равна либо единице (прямой ход), либо
(диагональный ход), то длина всего
пути заведомо не меньше
Путь длины
изображён на рисунке.

Покажем, что длина пути короля не может быть больше Рассмотрим два соседних выхода A и B короля на границу доски.
Если эти граничные поля не соседние, то участок пути короля между ними разбивает доску на две части, в каждой из которых есть целые
клетки. Но тогда король не сможет пройти из одной части в другую, что противоречит условию. Значит, поля A и B — соседние и,
следовательно, разного цвета. Так как при диагональных ходах цвет поля не меняется, то между каждыми двумя соседними
выходами на границу должен быть прямой ход. Поскольку граничных полей
то и выходов на границу — тоже
и,
следовательно, прямолинейных ходов не меньше
Следующий рисунок показывает„ что можно обойтись ровно
"прямыми"ходами.

Наименьшая длина — наибольшая —
Ошибка.
Попробуйте повторить позже
В двух коробках лежат шарики: красные, синие и белые. Если вытащить 3 шарика из первой коробки, то среди них обязательно найдётся синий. Если вытащить 4 шарика из второй коробки, среди них обязательно будет красный. Если взять любые 5 шариков (только из 1-ой, только из 2 -ой или из двух коробок одновременно), то среди них обязательно найдется белый шарик. Какое наибольшее количество шариков может быть в двух коробках вместе?
Источники:
Оценка.
Рассмотрим условие на первую коробку. Из него следует, что в первой коробке не синих шариков не больше двух: иначе мы могли бы набрать 3 шарика, среди которых нет синих.
Рассмотрим условие на вторую коробку. Из него аналогично следует, что во второй коробке не красных шариков не больше трёх.
Таким образом, всего шариков не более , если не учитывать синие шарики из первой коробки и красные шарики из
второй.
Наконец, из условия на две коробки сразу следует, что всего не белых шариков не более четырёх. В частности, синих шариков из
первой коробки и красных шариков из второй в сумме не больше четырёх. Поэтому общее число шариков не превосходит
.
Пример.
Положим в первую коробку 2 белых шарика и 2 синих, а во вторую 2 красных шарика и 3 белых. Нетрудно убедиться, что все условия выполняются.
Ошибка.
Попробуйте повторить позже
В ресторанчик надо доставить несколько бочек кислого молока общей массой 10 тонн. Каждая бочка весит не более 1 тонны. Какого наименьшего количества трехтонок для этого заведомо хватит?
Четырёх трёхтонок может не хватить. Действительно, если у нас будет 13 бочек весом т каждая, то больше трёх бочек погрузить не
удастся
, а значит, в четьре трёхтонки будет погружено 12 бочек и одна останется.
Докажем, что пяти трёхтонок хватит при любом раскладе. Для этого построим алгоритм погрузки. Постепенно, ящик за ящиком начинаем грузить первую машину. Естественно, в некоторый момент времени, окажется, что после погрузки очередного ящика общая масса погруженного станет больше 3 т. Тогда снимаем обратно последний из ящиков - после этого в машине уже будет не более трёх тонн и не менее двух тонн (из-за того, что перед снятием последнего ящика масса груза была более трёх тонн, а снятый ящик весил не более тонны). Точно также поступаем со второй, третей и четвёртой машинами. Получим четыре автомобиля. В каждом из которых не менее 2 т груза, т.е. общая масса груза в них - не менее 8 т. Это значит, что масса оставшегося груза - не более 2 тонн и мы спокойно грузим его в последнюю машину.
Ошибка.
Попробуйте повторить позже
Рассмотрим узлы (вершины) клеток доски. Кораблик размера занимает ровно
узла. При этом каждый узел будет
занят ровно одним кораблем, потому что по правилам морского боя корабли не смежны по сторонам и вершинам клеток
доски.
Также заметим, что всего у доски будет
узлов.
Тогда на доске можно разместить не более
корабликов.
а) При получаем оценку, что кораблей не более
Так как число кораблей целое, то их максимум .
Пример на кораблей:

b) При ,
получаем оценку, что кораблей не более
Так как число кораблей целое, то их максимум .
Пример на кораблей:

a)
b)
Ошибка.
Попробуйте повторить позже
У Вити есть 9 альбомов с марками, причём в любых двух альбомах количество марок различается. Витя хочет отдать сестре один или два пустых альбома на её выбор. При этом Витя обнаружил, что, какой бы один или какие бы два альбома ни попросила сестра, марки из них можно распределить по остальным альбомам так, что во всех оставшихся семи или восьми альбомах станет поровну марок. Изначально у Вити меньше всего марок в красном альбоме. А какое минимальное количество марок может быть в синем альбоме?
Источники:
Подсказка 1
Подумаем, а как использовать условие на то, что можно разложить любой альбом по всем остальным альбомам так, чтобы марок в них было поровну? Какой альбом хочется попробовать расформировать?
Посмотрим, какое минимальное количество марок может изначально быть у Вити в красном альбоме.
_________________________________________________________________________________________________________________________________________________________________________________
Оценка: Упорядочим альбомы по количеству марок, начиная с наименьшего. Если во втором по количеству альбоме марок, то в
следующих не менее чем
. После расформирования первого альбома в каждом из остальных будет не менее
марок, то есть в них надо добавить не менее чем
марок.
Пример: 28, 35, 36, ..., 42. Суммарное количество марок тут делится на 7 и на 8 (
), поэтому можно сделать как 8
альбомов по 42 марки, так и 7 по 48 марок.
_________________________________________________________________________________________________________________________________________________________________________________
Итак, тогда общее число марок не меньше , к тому же кратно 7 и 8 , а потому не меньше
.
Если в этой сумме заменить
на
, то получим пример к ответу 32.
Предположим теперь, что в синем альбоме 31 марка или меньше. Тогда в красном не более 30 марок. В то же время общее количество
марок равно , где
. После расформирования красного альбома в остальных нужно сделать ровно по
марок. Значит, изначально
в каждом альбоме не более
марок. В синий альбом придётся добавить не менее
марок, а в остальные
суммарно не менее чем
марку. Однако в сумме это не менее 32 марок, а в красном альбоме лишь
30.
Ошибка.
Попробуйте повторить позже
Вредный учитель даёт ученикам тест из 12 вопросов, на каждый из которых надо ответить «да» или «нет». Учитель не только вредный, но и нечестный, поэтому «правильные» ответы он определяет только после того, как ученики сдадут работы. При этом учитель стремится выбрать «правильные» ответы так, чтобы ни один из учеников не угадал больше половины ответов. При каком наибольшем количестве учеников учитель гарантированно сумеет это сделать?
Источники:
Подсказка 1
Чтобы учитель смог провернуть свой коварный замысел, нужно чтобы возможных вариантов ответа было больше, чем учеников. Поэтому нам нужно рассмотреть цепочки ответов, но какой длины они должны быть?
Подсказка 2
Нам нужно, чтобы ученики ответили не более, чем на половину вопросов. А для какого числа очень легко посчитать половину? Для двойки! Рассмотрите цепочки ответов длины 2!
Подсказка 3
Существует 4 варианта ответить на два вопроса. Тогда сколько должно быть школьников, чтобы учитель смог сделать один из вариантов правильным? Дорешайте задачу и не забудьте про пример!
Если учеников три (или меньше), то учитель справится. Действительно, на первые два вопроса возможны 4 варианта ответа: ++, +-, –, -+. Поскольку учеников не больше трёх, то какую-то из этих комбинаций никто не выбрал, её-то учитель и объявляет «правильной». Так же он поступает с каждой следующей парой ответов. В результате у каждого ребёнка не больше половины верных ответов.
Четыре ученика смогут «обыграть» учителя. Для этого им надо разделить вопросы на две группы нечётного размера (например, первые 5 и последние 7 вопросов) и дать такие ответы: ++++++++++++,————, +++++——-,—–+++++++. Тогда найдётся ребёнок, угадавший больше половины ответов как в первой группе, так и во второй.
Ошибка.
Попробуйте повторить позже
В какое наименьшее количество цветов можно покрасить натуральные числа так, чтобы любые два числа, отличающиеся на два или в два раза, были покрашены в разные цвета?
Оценка. Рассмотрим числа очевидно их нельзя покрасить в два цвета.
Пример. Раскрасим числа в разные цвета, а дальше для каждого числа
будем красить его в цвет отличный от цветов чисел
и
Следовательно, мы сможем раскрасить все числа в три цвета.
В цвета
Ошибка.
Попробуйте повторить позже
В коробке лежат карандаши цветов. Известно, что если не глядя взять
карандашей, то среди них обязательно найдутся
карандаши
разных цветов. Какое наибольшее количество карандашей могло быть в коробке?
Поскольку среди любых 100 карандашей есть хотя бы 7 разных цветов, то в любой шестёрке цветов карандашей суммарно не больше 99 (иначе можно взять 100 карандашей только среди этих шести разных цветов, а по условию обязательно должен найтись седьмой).
Обозначим количества карандашей разных цветов за
Если то получаем
противоречие с выводом выше. Значит,
Тогда суммарно в коробке карандашей
Может ли быть ровно 1603 карандаша? Да, например, если было 19 карандашей одного цвета ( и по 16 карандашей всех
остальных цветов (
Ошибка.
Попробуйте повторить позже
На шахматной доске стоят 10 шахматных фигур – слоны и ладьи. Никакая фигура не бьёт ни одну другую. Какое наименьшее количество слонов может быть среди них?
Заметим, что ладей не может быть больше восьми, поскольку тогда по принципу Дирихле какие-то две стоят на одной вертикали и бьют друг друга. Если ладей ровно восемь, то они должны занимать все вертикали, поэтому слонов будет поставить некуда (их обязательно будет бить какая-то ладья). Отсюда следует вывод, что ладей на доске не более семи. Если ладей ровно семь, то они бьют 7 вертикалей и 7 горизонталей, откуда для слонов остаётся всего одна свободная клетка, поэтому ровно 7 также не может быть. Значит, ладей не более шести.
Ровно шесть ладей и четыре слона могут стоять, например, так:
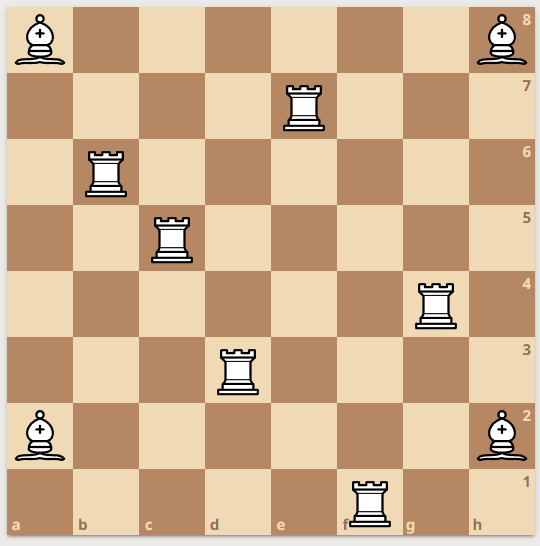
4
Ошибка.
Попробуйте повторить позже
На одной стороне каждой из 100 карточек написали одно из натуральных чисел от 1 до 100 включительно (каждое число записано ровно на одной карточке), после чего перевернули их обратными сторонами вверх и разложили в произвольном порядке на столе. За один вопрос Вася может указать на две любые карточки, после чего получает от ведущего ответ, являются ли записанные на них числа соседними (отличающимися на 1). За какое минимальное число вопросов Вася может гарантированно назвать хотя бы одну пару карточек, на которых написаны соседние числа?
Источники:
Подсказка 1
Поймём, что эта задача на оценку + пример! Чтобы придумать пример, подумайте о том, сколько соседей у каждого числа от 1 до 100.
Подсказка 2
Да, у каждого числа от 2 до 99 включительно — два соседа, а у чисел 1 и 100 — один сосед! Тогда можно увидеть алгоритм: задавать вопросы про одну и ту же карточку, постоянно меняю другую карточку. Какой ответ даёт этот алгоритм?
Подсказка 3
Верно, при таких действиях за 98 вопросов мы точно сможем назвать соседние числа! Осталось доказать, что за меньшее число вопросов доказать нельзя. Для этого нужно подумать о задаче в терминах теории графов. Тогда карточки — это вершины, а вопросы — это ребра! Что нужно найти в графе, чтобы доказать, что 98 — искомый ответ на задачу?
Подсказка 4
Да, надо найти Гамильтонов путь (такой путь, в котором каждая вершина встречается ровно один раз) по всем вершинам в графе, в котором ни одно ребро не является ребром, которое появилось вследствие вопроса Васи! Попробуйте посмотреть на задачу при малых n и доказать это утверждение по индукции!
Подсказка 5
База индукция тривиальна, поэтому давайте сразу подумаем о переходе! Такс, а что если посмотреть на вершину из которой выходит ровно одно ребро? А что будет в графе без неё? Можно ли в нём построить нужный нам путь?
Подсказка 6
Да. если есть такая вершина, то задача легко решается по индукции, ведь мы всегда можем переходить от случая с n вершинами к n+1 вершине с помощью добавления одного нужного нам ребра! Но вот незадача: что если нет вершин, из которых ихходит ровно одно ребро?
Подсказка 7
А если нет вершин с степенью 1, то можно точно утверждать, что есть хотя бы две вершины со степенью 0. Остаётся посмотреть на две этих вершин и еще одну вершину степень которой хотя бы 2!
Пример. Пусть Вася выберет какую-то карточку и задаст
вопросов, в каждом из которых он спросит про
и одну из
карточек, отличных от
Общее количество чисел, не соседних с числом, написанным на
не превосходит
если на
написано
или
и
если на
написаны числа от
до
Тогда либо в одном из
ответов будет дан
положительный ответ, и Вася нашёл нужную пару соседних чисел, либо все эти карточки содержат числа, не соседние с числом на
Следовательно, оставшаяся карточка содержит число, соседнее с числом на
Таким образом, Васе достаточно
вопросов.
Оценка. Докажем, что, если Вася задаст всего любых вопросов, он может не найти ни одной пары карточек с соседними числами.
Предположим противное, что задав некоторые
вопросов он смог точно указать на пару карточек с соседними числами. Переведём
задачу на язык теории графов. Карточки будем считать вершинами графа
а заданные Васей вопросы – рёбрами
(синими рёбрами),
соединяющими соответствующие пары карточек. К этим рёбрам нужно добавить ещё одно, соответствующее той паре карточек, на которых
написана пара соседних, по версии Васи, чисел. Теперь нужно доказать, что вершины
могут быть занумерованы в таком порядке, что ни
одно ребро не соединяет две вершины с соседними номерами. То есть, нужно дорисовать в графе путь из
рёбер, проходящий
последовательно по всем
вершинам, и не содержащих ни одного из
«Васиного» синего ребра. Это будет означать, что Васина
догадка не верна. Назовём такой путь красным и будем строить его методом математической индукции по числу вершин графа
Предположим, что в любом графе с числом вершин в котором проведено не больше
синих рёбер, существует красный
путь
по всем вершинам, не содержащий синих рёбер. Построим красный путь в
1) Пусть в есть «крайняя» вершина
из которой выходит ровно одно ребро
В графе
полученном из
удалением
вершины
и ребра
число вершин равно
а рёбер – не больше
выполнено предположение индукции, поэтому
в
можно построить красный путь длины
с началом в вершине
и концом в вершине
Тогда ребро
не
соединяет вершину
с одной из
или
проведя красное ребро из
в эту вершину, получим красный путь длины
в
2) Пусть в нет вершин, из которых выходит ровно одно ребро. В таком случае все синие рёбра инцидентны в сумме
вершинам
степени не меньше
каждая, следовательно, среди них не больше
различных. Следовательно, в
не меньше двух вершин
из
которых не выходит ни одного синего ребра. Удалим из
вершины
и два ребра, выходящие из некоторой четвёртой вершины
(но
не саму вершину). Полученный граф
снова удовлетворяет предположению индукции и в нём можно построить красный путь длины
с началом в вершине
и концом в вершине
Если он не проходит через
или проходит, но не проходит через удалённые рёбра,
соединим
с
и
с
и получим красный путь в
длины 99. В оставшихся случаях, обозначим за
и
вторые концы удалённых
рёбер. Если красный путь в
проходит через
заменим этот фрагмент на
Если он проходит только
через одно удалённое ребро, скажем, через
заменим его на
В обоих случаях получится красный путь в
База индукции - случаи графов с 3 и 4 вершинами - очевидна.
Ошибка.
Попробуйте повторить позже
В понедельник в школьную библиотеку пришло 8 учеников, во вторник — в среду —
в четверг —
в пятницу —
Никто из
учеников не был в библиотеке два дня подряд. Какое наименьшее количество учеников побывало в библиотеке с понедельника по
пятницу?
Подсказка 1
Нам говорят, что никто из учеников не был два дня подряд! Что можно сказать про учеников, которые были в первый и второй день?
Подсказка 2
Да, все эти ученики различны! То есть, мы нашли уже 12 различных учеников. Давайте заметим, что в четвертый день было всего 2 ученика, поэтому это наталкивает на мысль, что можно построить пример! Попробуем это сделать
Подсказка 3
Верно, в третий день можно отправить шесть учеников, которые были в первый день! В четвертый день отправим оставшихся 2 из первого дня. А на пятый день, уже можно отправить всех тех, кто был в третий день, кроме одного!
Понятно, что в первый день пришли различных людей. Раз никто не посещал библиотеку
дня подряд, то во второй пришли
новых
учеников, которые не пришли в первый день. Тогда можно сказать, что учеников хотя бы
Попробуем построить пример. Пронумеруем
каждого ученика от
до
В первый день пришли:
Во второй день пришли:
В третий день пришли:
В четвёртый день пришли:
В пятый день пришли:
Ошибка.
Попробуйте повторить позже
Однажды друзей, живущих в разных уголках земного шара, захотели обменяться друг с другом новостями. Для этого они собираются
устроить
видеовстреч, на каждой из которых каждый человек расскажет всем свои новости, а также все новости других людей, которые
он узнал ранее.
Для видеовстреч было предложено дней, но оказалось, что каждый из друзей может присутствовать только в какие-то
из них.
При каком наименьшем натуральном
можно гарантированно выбрать
дней для видеовстреч из предложенных
так, чтобы каждый
узнал новости каждого?
(Между предложенными днями у людей новых новостей не возникает, и никак иначе они друг с другом не общаются. В каждый из предложенных дней проходит одна видеовстреча, на которой собираются все, кто может в этот день присутствовать.)
Оценка. Приведём пример ситуации, в которой 4 дней не хватит. Пусть у каждого из 45 людей будет своя, не совпадающая с другими
людьми, пара дней, в которые он не может участвовать во встрече. Так как количество способов выбрать пару дней из 10
предложенных равно , то для любой пары дней найдётся человек, который не может присутствовать ровно в
эту пару дней. Предположим, что мы смогли выбрать какие-то 4 дня так, чтобы каждый узнал все новости. Но тогда
существует человек
, который не может присутствовать в первые два дня из этих четырёх, а также человек
, который
не может присутствовать в последние два из этих четырёх дней. Заметим, что тогда
не сможет узнать новостей
.
Противоречие.
Пример. Теперь поймём, что 5 дней всегда точно хватит. Выберем 5 дней произвольным образом. Докажем, что любые два человека будут вместе присутствовать на какой-то встрече. Действительно, среди этих 5 дней есть не более 2 дней, в которые не может присутствовать первый, а также не более 2 дней, в которые не может присутствовать второй. Значит, найдётся день, в который могут присутствовать оба человека. Таким образом, каждая пара людей сможет обменяться новостями, то есть каждый узнает новость каждого.
При
Ошибка.
Попробуйте повторить позже
В комоде лежат носка:
белых и
чёрных. Раз в минуту Марина подходит к комоду и вытаскивает из него носок. Если в какой-то
момент Марина достаёт суммарно больше чёрных носков, чем белых, она восклицает: “Наконец-то!” — и заканчивает процесс. Какое
наибольшее число носков может достать Марина, прежде чем воскликнет: «Наконец-то!»? В ответе учитывается носок, который Марина
достала последним.
Источники:
Подсказка 1
Рассмотрите случай, когда Марине очень не везёт с чёрными носками!
Подсказка 2
Что будет, если Марина сначала подряд будет вытаскивать только белые носки? До каких пор она сможет так делать и сколько чёрных ей пригодится еще достать, чтобы обрадоваться?
Подсказка 3
Сначала она может достать максимум 8 белых!
Если Марина достанет 17 носков, то среди них будет не больше 8 белых, а значит - хотя бы 9 чёрных. Поэтому в этот момент она точно воскликнет «Наконец-то!».
С другой стороны, если она достанет всего 16 носков, ей «может не повезти»: если она последовательно достаёт белый носок, чёрный носок, белый носок, чёрный носок, .... В этой ситуации после каждого чётного вытащенного носка чёрных и белых носков будет поровну, а после каждого нечётного - больше белых.
Ошибка.
Попробуйте повторить позже
В классе учеников. Известно, что у любых двух девочек класса количество друзей-мальчиков из этого класса не совпадает. Какое
наибольшее количество девочек может быть в этом классе?
Подсказка 1
Для начала попробуйте построить пример - например, если в классе x девочек, то их возможные значения количества дружб (минимально возможные) - 0, 1, 2 .... (х-1). Какой вывод мы можем из этого сделать?
Подсказка 2
Тогда у нас в классе при х девочках минимум х-1 мальчик. А теперь осталось понять, какое максимальное количество их может быть, найти х и не забыть пример!
Пусть девочек хотя бы . Так как у разных девочек разное количество друзей-мальчиков, то у девочки с наибольшим количеством
друзей-мальчиков таких друзей хотя бы
(так как может быть девочка, которая не дружит с мальчиками). Значит, мальчиков хотя бы
и всего детей хотя бы
?!
Значит, девочек не больше, чем . Докажем, что ровно
может быть. Пронумеруем мальчиков и девочек и скажем, что
-ая девочка дружит с
-ым мальчиком, если
. Тогда у первой девочки нет друзей, у второй девочки один друг и
т.д.
Ошибка.
Попробуйте повторить позже
В какое наибольшее число цветов можно раскрасить доску так, чтобы каждая клетка граничила по стороне хотя бы с двумя
клетками своего цвета?
Подсказка 1
Начать решение этой задачи можно с подбора примера - попробуйте интуитивные раскраски. Как можно расположить клетки одного цвета, чтобы любая клетка имела хотя бы двух покрашенных соседей? Например, можно попробовать располагать одноцветные клетки в квадрат 2*2
Подсказка 2
Взяв шахматную раскраску из квадратов 2*2 мы можем получить пример на 16, попробуем доказать, что он максимальный. Для этого логично использовать метод доказательства от противного. Что следует из наличия в таблице из 64 клеток хотя бы 17 различных цветов?
Пример. Разделим большой квадрат на 16 квадратиков и каждый из них закрасим в свой цвет. Тогда у каждой клетки есть два
соседа по стороне в квадрате того же цвета.
Оценка. Пусть можно раскрасить в 17 цветов. Тогда по принципу Дирихле найдётся цвет, в который раскрашены не более 3 клеток. Так как у каждой клетки должно быть 2 соседа того же цвета, то клеток может быть ровно 3. Но каждые 2 из этих трёх должны быть соседними?! Противоречие.
Ошибка.
Попробуйте повторить позже
Даны пять утверждений: “ — простое число”, “
— простое число”, “
— простое число”, “
— простое число”, “
— простое
число”. Какое наибольшее количество из них могут быть истинными одновременно?
Подсказка 1
Здесь у нас не очень большое поле для выбора ответа - от 0 до 5. Наверное, придумать пример, чтобы выполнялась часть утверждений - не очень сложно. (Можете попробовать). Выполнение всех 5 одновременно выглядит проблематично. Давайте пойдем сверху и попробуем доказать, что 5 одновременно не получится.
Подсказка 2
Нам нужно взять несколько утверждений и получить противоречие. Мы знаем, что х, у, х+у - простые числа. Попробуйте подумать, часто ли в жизни случается, что сумма двух простых чисел - простое число?
Оценка
Предположим, что все пять условий могут быть выполнены. Тогда числа ,
и
простые, но при этом одно из них чётное (так
как их сумма чётная, а сумма трёх нечётных чисел всегда нечётная).
Так как , то оно не
. Значит, четное или
, или
. Не умаляя общности, пусть
. Тогда число
чётное и
простое, то есть
, но тогда
?! Значит, правильных утверждений не более
.
Пример
Пусть и
. Тогда
,
и
. Получаются четыре верных условия из пяти (составным получилось
только
).
Ошибка.
Попробуйте повторить позже
В беседе курса “Боталка” 1337 участников. У каждого из них не больше трёх друзей. Дмитрий Алексеевич узнал, кто с кем дружит, и теперь хочет разбить одну беседу на несколько. Если два друга оказываются в одной беседе, то они немедленно начинают спамить. Какое наименьшее количество бесед нужно создать, чтобы спам прекратился (то есть любые два друга оказались в разных беседах)?
Подсказка 1
В данной задаче стоит начать с оценки снизу, то есть подумать, сколько минимум может быть бесед. Как думаете, скольких бесед точно не хватит, чтобы рассадить компанию из четырёх людей, в которой каждый знает каждого?
Подсказка 2
По принципу Дирихле, если мы возьмём три беседы, то в одной из них окажется не менее двух друзей, значит, три беседы будет недостаточно. Подумайте, получится ли распределить всех участников Боталки по четырём беседам, чтобы ни в одной из них не нашлось двух друзей!
Меньше четырёх бесед не хватит, ведь в соответствии с условием задачи могут найтись такие четыре ботальщика, что каждый из них знает
остальных трёх (то есть каждый человек дружит с остальными тремя). Эту компанию друзей нужно рассадить по разным беседам.
Очевидно, для них не хватит (или меньше) бесед, поскольку в какой-то окажутся двое и начнут спамить стикерами и флудить на не
связанные с обсуждением задач темы.
На беседы разделить ребят можно. Для этого Дмитрий Алексеевич может последовательно выбирать человека и смотреть на текущие
списки людей из бесед. У каждого ботальщика не больше трёх друзей, поэтому есть не больше трёх бесед, в которых уже находятся друзья
рассматриваемого человека. Значит, есть хотя бы одна беседа, в которой ботальщик пока никого не знает. Туда его и надо поместить (при
наличии нескольких таких бесед можно выбрать любую).
Ошибка.
Попробуйте повторить позже
Какое наименьшее число клеток доски нужно покрасить в чёрный цвет, чтобы в любом уголке из трёх клеток была хотя бы одна
закрашенная клетка?
Оценка: Поделим доску на квадраты , тогда в каждом из них должны быть закрашены хотя бы
клетки, потому что иначе в нём
найдётся уголок, который не содержит закрашенных, отсюда их не менее
.
Пример: Покрасим все строки доски с нечётными номерами ( клетки). Любой уголок содержит клетки двух каких-то соседних строк,
потому в нём будут закрашенные.



