04 Законы сохранения в механике
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
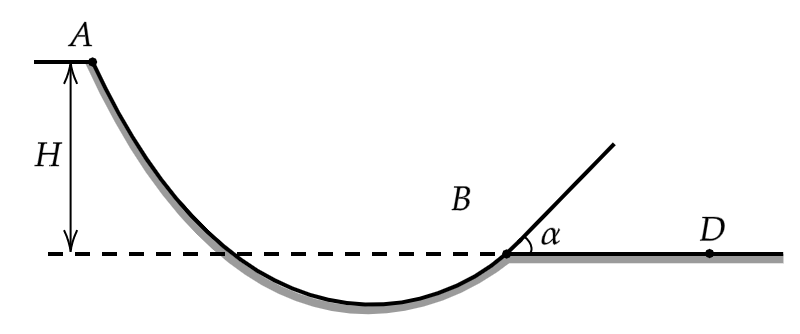
Шайба массой г начинает соскальзывать по поверхности желоба из точки А, расположенной на высоте
м. В точке
шайбы вылетает из желоба под углом
и падает в точке
. Найдите величину изменения механической энергии в
процессе движения шайбы по желобу, если
м. Сопротивлением воздуха пренебречь. Какие законы Вы используете для
решения задачи? Обоснуйте их применение.
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Шайба движется поступательно, её размеры малы по сравнению с размерами установки, будем описывать шайбу моделью материальной точки.
3. После отрыва от желоба шайба движется только под действием силы тяжести в отсутствии сопротивления воздуха. Сила тяжести является причиной ускорения свободного падения, направленного вертикально вниз.
4. При движении тела его сорость в направлении не изменяется, так как в направлении данной оси силы не действуют и
движение по данной оси является равномерным и описывается формулами кинематики прямолинейного равноменого движения. По
вертикальной оси
тело обладает ускорением, поэтому движение по этой оси равноускоренное и описывается формулами
кинематики прямолинейного равноускоренного движения.
5. Так как сопротивление воздуха отсутствует, сила реакции опоры всюду перпендикулярна вектору скорости и ее работа равняется нулю, а также есть сила сопротивления со стороны желоба (по условию есть изменение механической энергии), выполняется закон изменения механической энергии.
6. За нулевой уровень потенциальной энергии примем уровень, на котором находится точка .
Решение
В процессе движения по желобу будет справедлив закон изменения механической энергии
где – потенциальная энергия в точке
,
– кинетическая энергия в точке
, а
– изменение
механической энергии в процессе движения по желобу. Расписав энергии по формулам получим:
Движение шайбы после вылета из желоба рассмотрим с точки зрения кинематики. Движение по оси, направленной вдоль
поверхности земли будет равномерное, а движения по оси, перпендикулярной поверхности, будет равнозамедленное, с ускорение .
Напишем уравнение координаты в точке
. Пусть ось Ох направлена вдоль поверхности, ось Оу направлена перпендикулярно
поверхности движения. Тогда
|
|
где и
– начальная скорость,
– ускорение тела.
|
|
где – скорость шайбы в точке
,
– время полета шайбы. Выразим из второго уравнения время и подставим его в
первое.
Выразим из последнего уравнения
Подставим скорость в точке в закон сохранения энергии и выразим изменение механической энергии
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к шайбе модели материальной точки
3. Обосновано применение формул кинематики прямолинейного равномерного и равноускоренного движения
4. Обосновано применение закона изменения механической энергии
5. Введен нулевой уровень потенциальной энергии
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: закон сохранения энергии и формулы
кинематики движения тела, брошенного пооуглом к горизонту);
II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением
обозначений констант, указанных в варианте КИМ, и обозначений величин, используемых в условии
задачи);
III) проведены необходимые математические преобразования и расчеты, приводящие к правильному
числовому ответу (допускается решение «по частям» с промежуточными вычислениями);
IV) представлен правильный ответ с указанием единиц измерения искомой величины
2 балла ставится если:
_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности, и
проведены необходимые преобразования. Но имеются следующие недостатки.Записи, соответствующие
пункту II, представлены не в полном объеме или отсутствуют.
ИЛИ
В решении лишние записи, не входящие в решение (возможно, неверные), не отделены от решения (не зачеркнуты; не заключены в скобки, рамку и т.п.).
ИЛИ
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) преобразования/ вычисления не доведены до конца.
ИЛИ
Отсутствует пункт IV, или в нем допущена ошибка
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Представлены только положения и формулы, выражающие физические законы, применение которых
необходимо для решения задачи, без каких-либо преобразований с их использованием, направленных на
решение задачи, и ответа.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решения задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла.
Ошибка.
Попробуйте повторить позже
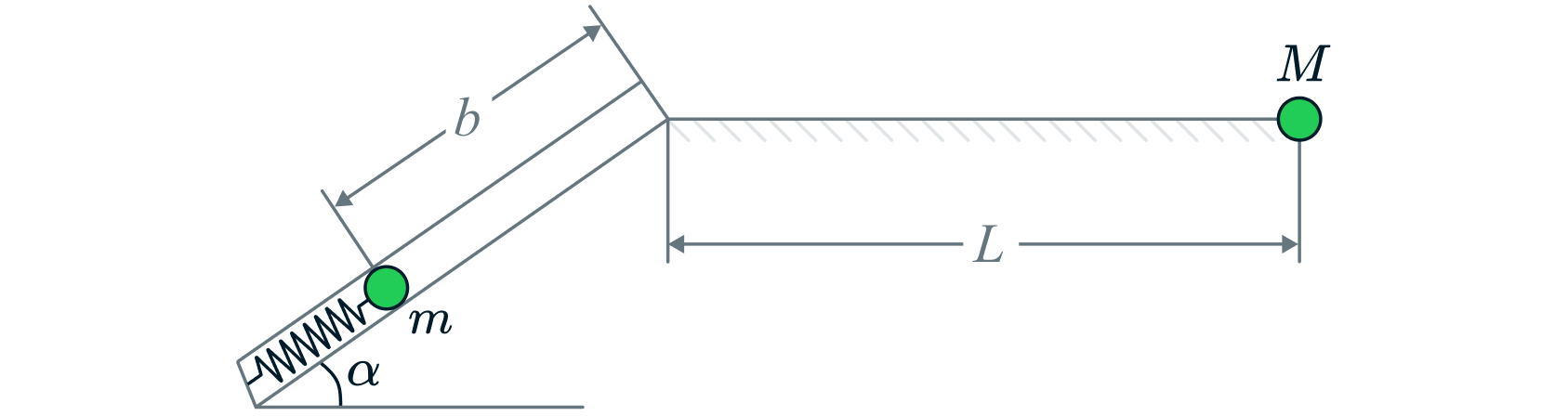
Пружинное ружье наклонено под углом к горизонту. Из ружья производят выстрел шарика, массой
он
проходит расстояние
и, вылетая из дула ружья, пролетает расстояние
от дула ружья и падает в точку
находящуюся на одном уровне с дулом ружья. Найдите энергию сжатия пружины. Трением о стенки дула пренебречь. Какие законы
Вы используете для решения задачи? Обоснуйте их применение.
Источники:
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Шарик движется поступательно, его размеры малы по сравнению с размерами установки, будем описывать шарик моделью материальной точки.
3. После отрыва от желоба шайба движется только под действием силы тяжести в отсутствии сопротивления воздуха. Сила тяжести является причиной ускорения свободного падения, направленного вертикально вниз.
4. При движении тела его сорость в направлении не изменяется, так как в направлении данной оси силы не действуют и
движение по данной оси является равномерным и описывается формулами кинематики прямолинейного равноменого движения. По
вертикальной оси
тело обладает ускорением, поэтому движение по этой оси равноускоренное и описывается формулами
кинематики прямолинейного равноускоренного движения.
5. Так как изменения механической энергии тела в ИСО равно работе всех непотенциальных сил, приложенных к телу, а в данной задаче единственной такой силой является сила нормальной реакции опоры, работа которой равна нулю, поскольку направление этой силы всюду перпендикулярно вектору перемещения при движении внутри стола, полня механическая энергия тела сохраняется.
6. За нулевой уровень потенциальной энергии примем уровень, на котором изначально находится шарик.
Решение
В процессе движения по дулу будет справедлив закон сохранения энергии
где – потенциальная энергия сжатой пружины,
– кинетическая энергия шарика при вылете из ружья, а
–
потенциальная энергия шарика при вылете из желоба. Расписав энергии по формулам получим:
Движение шайбы после вылета из дула рассмотрим с точки зрения кинематики. Движение по оси, направленной вдоль
поверхности земли будет равномерное, а движения по оси, перпендикулярной поверхности, будет равнозамедленное, с ускорение .
Напишем уравнение координаты в точке
. Пусть ось Ох направлена вдоль поверхности, ось Оу направлена перпендикулярно
поверхности движения.
|
|
Здесь – ускорение
|
|
где – скорость шарика при вылете из дула,
– время полета шарика. Выразим из второго уравнения время и подставим его в
первое.
Выразим из последнего уравнения
Подставим (2) в (1) и получим
| Критерии оценивания выполнения задачи | Баллы |
| Критерий 1 | |
| Верно обоснована возможность испольования законов | 1 |
| (закономерностей). В данном случае: выбор ИСО, модель материальной точки, возможность применения закона сохранения энергии | |
| В обосновании возможности использования законов | 0 |
| (закономерностей) допущена ошибка | |
|
ИЛИ
| |
| Обоснование отсутствует | |
| Критерий 2 | |
| Приведено полное решение, включающее следующие элементы: | 3 |
| I) записаны положения теории и физические законы, | |
| закономерности, применение которых необходимо для решения | |
| задачи выбранным способом (в данном случае - закон сохранения изменения и сохранения механической энергии с учётом энергии сжатой пружины, формулы кинематики тела, брошенного под углом к горизонту); | |
| II) описаны вновь вводимые в решении буквенные обозначения | |
| физических величин (за исключением обозначений констант, | |
| указанных в варианте КИМ, обозначений величин, используемых | |
| в условии задачи, и стандартных обозначений величин, | |
| используемых при написании физических законов); | |
| III) проведены необходимые математические преобразования | |
| и расчёты (подстановка числовых данных в конечную формулу), | |
| приводящие к правильному числовому ответу (допускается решение | |
| «по частям» с промежуточными вычислениями); | |
| IV) представлен правильный ответ с указанием единиц измерения | |
| фиизческой величины | |
| Правильно записаны все необходимые положения теории, | 2 |
| фиизческие законы, закономерности, и проведены необходимые | |
| преобразования, но имеется один или несколько из следующих | |
| недостатков. | |
|
| |
| Записи, соответствующие пункту II, представлены не в полном | |
| объёме или отсутствуют. | |
|
И(ИЛИ)
| |
| В решении имеются лишние записы, не входящие в решение | |
| (возможно, неверные), которые не отделены от решения и не | |
| зачёркнуты | |
|
И(ИЛИ)
| |
| В необходимых математических преобразованиях или вычислениях | |
| допущены ошибки, и(или) в математических преобразованиях/ | |
| вычислениях пропущены логически важные шаги. | |
|
И(ИЛИ)
| |
| Отсутствует пункт IV, или в нём допущена ошибка (в том числе | |
| в записи единиц измерений величины) | |
| Представлены записи, соответствующие одному из следующих | 1 |
| случаев. | |
| Представлены только положения и формулы, выражающие | |
| физические законы, применение которых необходимо для решения | |
| данной задачи, без каких-либо преобразований с их | |
| использованием, направленных на решение задачи. | |
|
ИЛИ
| |
| В решении отсутствует ОДНА из исходных формул, необходимая | |
| для решения данной задачи (или утверждение, лежащее в основе | |
| решения), но присутствуют логически верные преобразования | |
| с имеющимися формулами, направленные на решение задачи. | |
|
ИЛИ
| |
| В ОДНОЙ из исходных формул, необходимых для решения данной | |
| задачи (или в утверждения, лежащем в основе решения), допущена | |
| ошибка, но присутствуют логически верные преобразования | |
| с имеющимися формулами, направленные на решение задачи | |
| Все случаи решения, которые не соответствуют вышеуказанным | 0 |
| критериям выставления оценок в 1, 2, 3 балла | |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
С какой начальной скоростью надо бросить мяч с высоты м, чтобы он при ударе об землю отскочил на высоту
м,
если потеря модуля импульса при ударе об землю равна
. Силами сопротивления воздуха пренебречь. Какие законы Вы
используете для решения задачи? Обоснуйте их применение.
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Мяч движется поступательно, его размеры малы по сравнению с размерами установки, будем описывать мяч моделью материальной точки.
3. Так как изменение механической энергии тела в ИСО равно работе всех непотенциальных сил, приложенных к телу, а в данном случае таких сил нет (сопротивлением воздуха пренебрегаем), то полная механическая энергия мяча при его движении сохраняется.
4. Исходя из условия можно записать связь между импульсами мяча до и после соударения с землей.
5. За нулевой уровень потенциальной энергии примем поверхность земли.
Решение
Запишем систему уравнений, состоящую из закона сохранения импульса и закона сохранения энергии
|
|
где – потенциальная энергия мяча на высоте
,
– кинетическая энергия шара на высоте
,
– кинетическая
энергия шара при столкновении с землей,
– импульс до столкновения с землей,
– импульс после столкновения с землей.
Расписав по формулам, получим
|
|
где – масса шарика,
– начальная скорость,
– скорость перед столкновением с землей,
– скорость после столкновения с
землей. Из второго уравнения скорость после столкновения равна
.
Запишем закон сохранения энергии при движении вверх до высоты
Выразим скорость
Значит
Подставим (2) и (3) в (1) и выразим начальную скорость.
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к шайбе модели материальной точки
3. Обосновано применение закон сохранения импульса
4. Обосновано применение закона сохранения энергии
5. Введен нулевой уровень потенциальной энергии
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: закон сохранения импульса в векторной
форме и в проекции на координатную ось, формула импульса материальной точки, закон изменения и
сохранения механической энергии, формула кинетической энергии материальной точки, формула
потенциальной энергии тела в однородном поле тяжести).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)
И (ИЛИ)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
И (ИЛИ)
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Ошибка.
Попробуйте повторить позже
Кусок пластилина скользит по столу навстречу бруску и сталкивается с ним. Скорости пластилина и бруска перед ударом
направлены взаимно противоположно и равны м/с и
м/с. Масса пластилина в 4 раза меньше массы бруска.
Коэффициент трения скольжения между бруском и столом
На какое расстояние переместятся слипшиеся брусок с
пластилином к моменту, когда их скорость уменьшится в 2 раза? Какие законы Вы используете для решения задачи? Обоснуйте их
применение.
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Кусок пластилина и брусок движутся поступательно, будем описывать их моделью материальной точки.
3. После столкновения бруска и пластилина образуется система "брусок + пластилин которая движется поступательно, её также можно считать материальной точкой.
4. Описывать соудраение будем при помощи закона сохранения импульса в горизонтальном направлении, так как соударение мгновенное и действием внешних сил в момент удара можно пренебречь.
5. Для описания последующего движения системы тел будем использовать закон сохранения энергии с учетом того, что часть энергии расходуется на преодоление силы трения между бруском и столом.
Решение
Запишем систему уравнений, состоящую из закона сохранения импульса и закона сохранения энергии
|
|
где – кинетическая энергия пластилина и бруска после столкновения,
– кинетическая энергия бруска и пластилина после
уменьшения скорости в 2 раза,
– импульс системы после столкновения,
и
– импульс бруска и пластилина
соответственно. Расписав по формулам, получим
|
|
где – скорость после столкновения,
– скорость, при уменьшении в два раза
,
– искомое расстояние
Из второго уравнения найдем скорость после столкновения
Так как , то
м/с Подставим в (1) найденные скорости и выразим расстояние
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телам и системе тел после взимодействия модели материальной точки
3. Обосновано применение закона сохранения импульса
4. Обосновано применение закона сохранения энергии
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: записан закон сохранения импульса, закон
сохранения энергии формула импульса, формула кинетической энергии).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)
И (ИЛИ)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
И (ИЛИ)
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Ошибка.
Попробуйте повторить позже
Пластилиновый шарик массой кг, подвешенный на нити длиной
м, отводят в сторону и отпускают. В нижней
точке качения шарик налетает на покоящийся брусок. В результате абсолютно неупругого соударения брусок приобретает скорость
м/с. Определите массу бруска
, если в момент столкновения натяжение нити было
Н. Какие законы Вы
используете для решения задачи? Обоснуйте их применение.
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Шарик имеет малые размеры, будем описывать его моделью материальой точки
3. Так шарик является материальной точкой, то для описания его движения будем использовать второй закон Ньютона относительно ИСО.
4. Процесс соударения яляется мгновенным, при этом в горизонтальном направлении не действуют никакие внешние силы, поэтому описывать соударение будем при помощи закона сохранения импульса в проекции на горизонтальную ось.
5. Шарик дижется по коружности, поэтому он будет обладать центростремительным ускорением направленным к центрту окружности вращения.
Решение
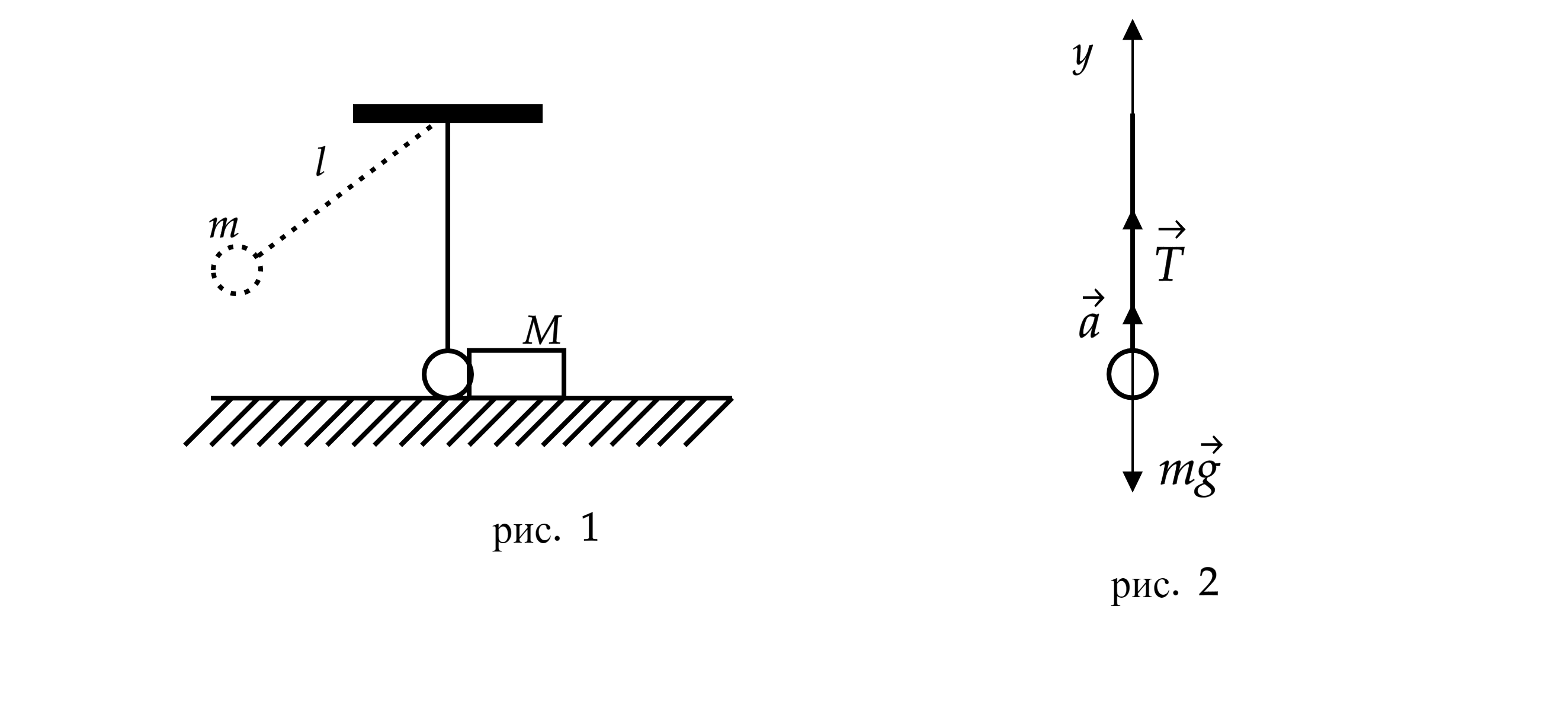
Запишем второй закон Ньютона в момент, когда шарик касается бруска (см. рис. 2)
В проекции на вертикальную ось, направленную вверх
где – сила тяжести,
– центростремительное ускорение,
– скорость шарика.
Распишем все составляющие закона по формулам и получим:
– скорость перед столкновением с бруском. Выразим скорость перед столкновением
Также запишем закон сохранения импульса при абсолютно неупругом ударе
где – импульс шарика,
– импульс бруска,
– импульс бруска и шарика после удара. Распишем все составляющие по
формулам, с учетом того, что брусок покоится
Выразим массу бруска
Подставим (1) в (2)
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность описания шарика моделью материальной точки
3. Обосновано применение второго закона Ньютона для описания движения шарика
4. Обосновано применение закона сохранения импульса
5. Обосновано наличие центростремительного ускорения
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: второй закон Ньютона, формула
центростремительного ускорения, закон сохранения импульса системы);
II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением
обозначений констант,указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при написании физических
законов);
III) проведены необходимые математические преобразования и расчёты, приводящие к правильному
числовому ответу (допускается решение «по частям» с промежуточными вычислениями);
IV) представлен правильный ответ с указанием единиц измерения искомой величины
2 балла ставится если:
_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности, и
проведены необходимые преобразования. Но имеются один или несколько из следующих
недостатков.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/ вычислениях пропущены логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Представлены только положения и формулы, выражающие физические законы, применение которых
необходимо для решения данной задачи, без каких-либо преобразований с их использованием,
направленных на решение задачи
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решения данной задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла
Ошибка.
Попробуйте повторить позже
Пуля массой кг и скоростью
м/с влетает в небольшое тело массой
, лежащее на вершине гладкой
полусферы. После их абсолютно неупругого столкновения бруска с пулей приходят в движение и скатываются с поверхности сферы,
на высоте
м тело отрывается от поверхности полусферы. Пренебрегая смещением сферы за удар, найдите радиус
полусферы. Высота отсчитывается от основания полусферы. Какие законы Вы используете для решения задачи? Обоснуйте их
применение.
Обоснование
1. Введем инерциальную систему отсчёта (ИСО), связанную с землей.
2. Пуля и тело имеют малые размеры по сравнению с установкой, значит можно описывать их моделью материальной точки. После
абсолютно неупругого соударения тела будут двигаться поступательно вместе, как единое целое, данную систему можно также
считать материальной точкой. Описывать соударение пули и тела будем при помощи закона сохранения импульса (так как
в горизонтальном направлении не действуют никакие силы во время удара, то он выполняется в горизонтальном
направлении).
3. Так как система тел является материальной точкой, то для описания её движения будем использовать второй закон Ньютона
относительно ИСО.
4. Применим закон сохранения энергии для описания движения тел, так как единственной не потенциальной силой является сила
реакции опоры, действующая на тело. Эта сила перпендикулярна вектору скорости в процессе движения, а значит ее мощность и
работа равняются нулю, полная механическая энергия системы тел не изменяется. За нулевой уровень потенциальной энергии
выберем уровень горизонтальной поверхности.
5. Так как система тел будет двигаться по окружности, то она будет обладать центростремительным ускорением, направленным к
центру окружности вращения.
Решение
.png)
Запишем второй закон Ньютона в момент, когда шарик оторвется от поверхности сферы, это означает, что сила реакции опоры будет равна нулю, и ускорение будет создаваться только силой тяжести. Запишем второй закон Ньютона
где – сила реакции опоры,
– центростремительное ускорение Так как
, то с учетом формулы
центростремительного ускорения
где
– скорость составного тела,
– радиус полусферы.
Тогда второй закон Ньютона на ось
С учетом того, что имеем
Запишем закон сохранения импульса в момент, когда пуля касается бруска
где – импульс пули,
– импульс составного тела после столкновения,
– скорость после
столкновения.
Закон сохранения импульса на горизонтальную ось
Отсюда скорость после столкновения
Также запишем закон сохранения энергии
где – кинетическая энергия после столкновения(на высоте
),
– потенциальная
энергия тела на высоте
,
– кинетическая энергия на высоте
,
– потенциальная
энергия на высоте
. Расписав все слагаемые по формулам получим
Подставим (1), (2) в (3)
Отсюда радиус полусферы
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телам и системе тел после взимодействия модели материальной точки
3. Обосновано применение второго закона Ньютона для описания движения системы тел
4. Обосновано применение закона сохранения энергии и закона сохранения импульса
5. Обосновано наличие центростремительного ускорения
6. Введен нулевой уровень потенциальной энергии
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: указано, что в момент отрыва груза сила
реакции опоры N = 0, записаны формулы второго закона Ньютона и закона сохранения импульса -
вначале в векторной форме, а затем в проекциях на выбранные координатные оси, формула
центростремительного ускорения материальной точки, закон сохранения и изменения механической
энергии, формулы для кинетической энергии материальной точки и потенциальной энергии тела в
однородном поле силы тяжести).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)
И (ИЛИ)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
И (ИЛИ)
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Ошибка.
Попробуйте повторить позже
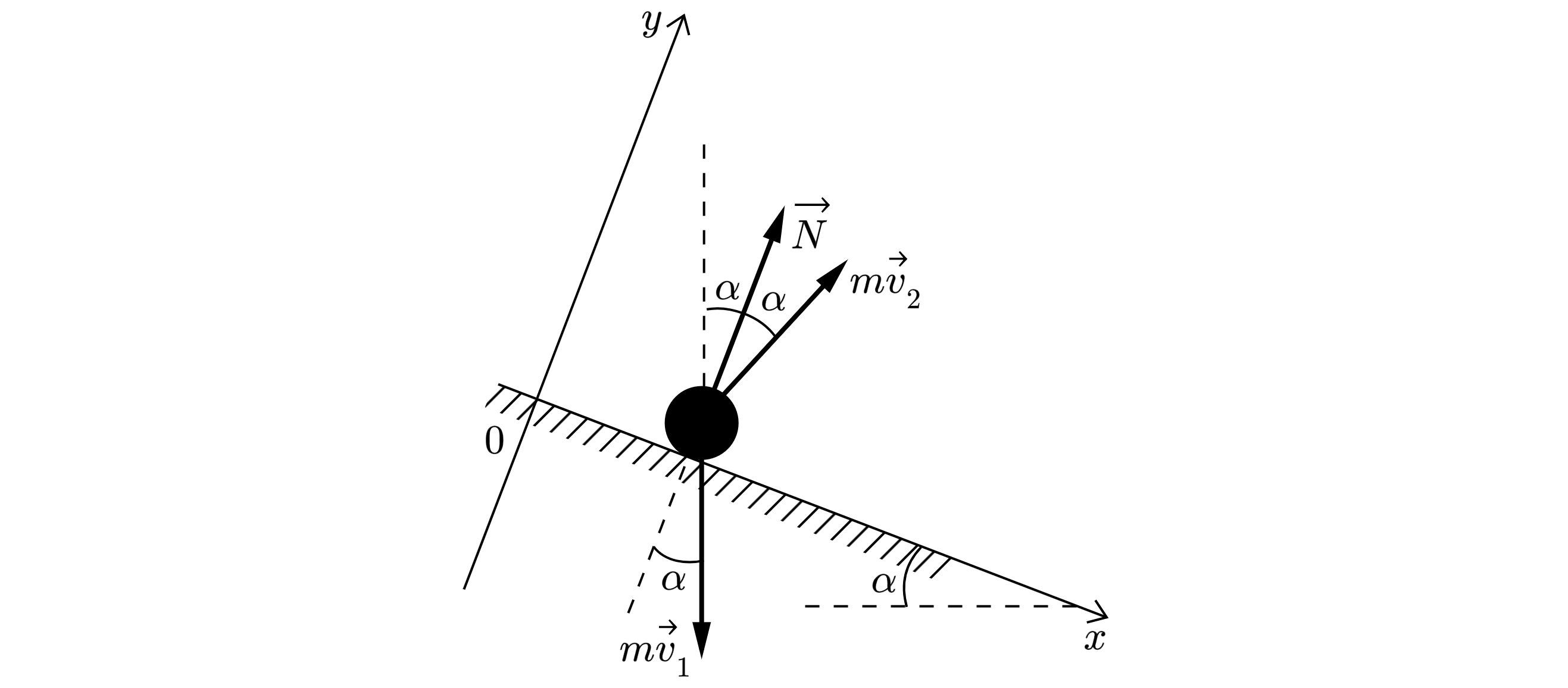
Шарик падает с высоты м над поверхностью Земли из состояния покоя. На высоте
м он абсолютно упруго ударяется
о доску, расположенную под углом
к горизонту (см. рисунок). На какую максимальную высоту
после этого удара
поднимется шарик от поверхности Земли? Сопротивлением воздуха пренебречь.
Обоснуйте применимость используемых законов к решению задачи.

Источники:
Обоснование
1. Рассмотрим задачу в системе отсчёта, связанной с Землёй. Будем считать эту систему отсчёта инерциальной
(ИСО).
2. Шарик движется поступательно, поэтому его можно принять за материальную точку.
3. При свободном падении шарика из начального положения на наклонную доску и после удара о доску до падения на землю на
шарик действует только потенциальная сила тяжести. Поэтому во введённой нами ИСО при этом движении сохраняется
механическая энергия шарика:
При абсолютно упругом ударе шарика о доску механическая энергия шарика сохраняется. Следовательно, сила
трения равна нулю, а направление силы реакции опоры , действующей на шарик при ударе, перпендикулярно
плоскости доски. Отметим, что
, так как время удара коротко, а изменение импульса шарика за время удара
конечно. Поэтому при описании удара пренебрегаем величиной
и записываем второй закон Ньютона для шарика в
виде:
Из того, что следует, что
. Из закона сохранения механической энергии при абсолютно упругом ударе
следует, что
, то есть модуль скорость шарика при таком ударе не меняется. Но точка
, и,
следовательно, угол падения шарика на доску равен углу отражения.
Решение

Движение шарика по вертикали описывается уравнением:
Здесь – начальная высота падения,
– начальная скорость тела,
– время движения,
– ускорение свободного
падения.
Тогда в спроецировав на вертикальную ось:
Скорость же описывается уравнением:
или
Объединив два уравнения, получим:
При отскоке его скорость по вертикали преобразуется в скорость по вертикали и горизонтали, по вертикали она станет равна
При это на максимальной высоте скорость равна 0, значит приращение высоты составит
Значит, высота подъема равна
с учетом (1) имеем
II способ
При падении шарика его потенциальная энергия на высоте преобразуется в кинетическую энергию на высоте
и
потенциальную на высоте
где – масса шарика,
– его скорость на высоте
.
Выразим скорость
При отскоке его скорость по вертикали преобразуется в скорость по вертикали и горизонтали, по вертикали она станет равна
При это на максимальной высоте скорость равна 0, значит приращение высоты составит
Значит, высота подъема равна
с учетом (1) имеем
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения закона сохранения механической энергии
3. Доказано равенство углов падения и отражения шарика
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: записаны законы кинематики
прямолинейного равноускоренного движения, закон сохранения механической энергии, формула
кинетической и потенциальной энергии).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)
И (ИЛИ)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
И (ИЛИ)
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Ошибка.
Попробуйте повторить позже
По гладкой наклонной плоскости, составляющей угол с горизонтом, скользит из состояния покоя брусок массой
г.
В тот момент, когда брусок прошёл по наклонной плоскости расстояние
м, в него попала и застряла в нём летящая
навстречу ему вдоль наклонной плоскости пуля. Скорость пули
м/с, масса пули
г. После попадания пули
брусок поднялся вверх вдоль наклонной плоскости на некоторое расстояние S от места удара. Определите расстояние
. Трение бруска о плоскость не учитывать. Какие законы Вы используете для решения задачи? Обоснуйте их
применение.
Источники:
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Брусок движется поступательно, его размеры малы по сравнению с размерами установки, будем описывать брусок моделью материальной точки.
3. По условию задачи сила трения отсутствует, ее работа равна нулю. Сила реакции опоры перпендикулярна вектору перемещения, значит работы не совершает. Значит, можно использовать закон сохранения энергии для описания движения бруска.
4. Процесс попадания пули мгновенный, значит, действием внешних сил можно пренебречь, можно применить закон сохранения импульса. Так как размеры пули меньше размера бруска, то ее также можно описывать моделью материальной точки.
5. За нулевой уровень потенциальной энергии примем уровень основания наклонной плоскости.
Решение
I способ
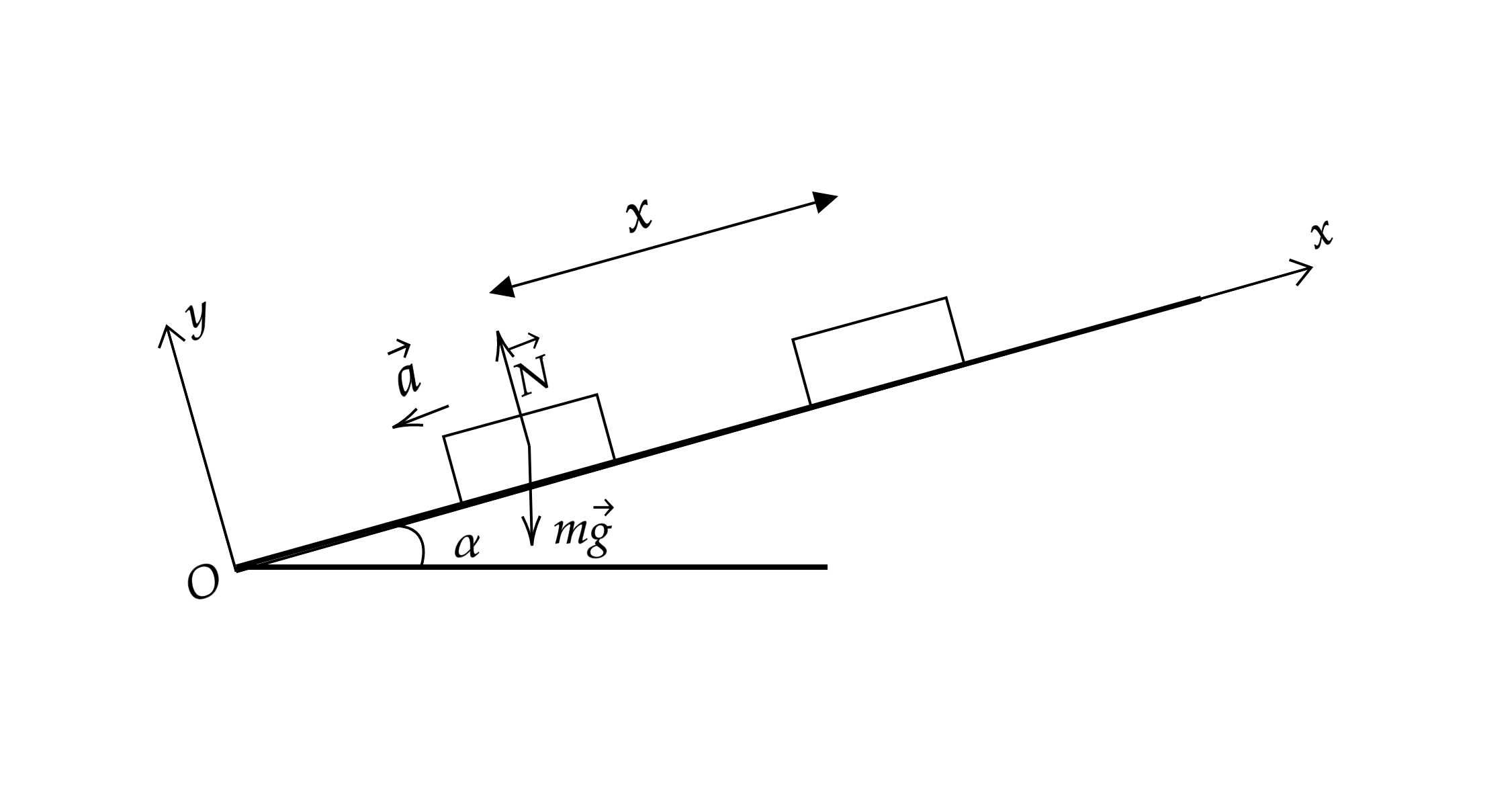
Запишем второй закон Ньютона
Здесь – сила реакции опоры,
– ускорение тела.
Спроецируем второй закон Ньютона на ось
Тело будет двигаться по наклонной поверхности с ускорением . У нас имеется формула расстояния
где и
– конечная и начальная скорости тела,
– ускорение тела.
В нашем случае тело двигается из состояния покоя, то есть
Отсюда конечная скорость равна
Воспользуемся законом сохранения импульса
Или в проекции на ось, совпадающую с движением тела
где – скорость составного тела сразу после попадания пули.
Отсюда
или же с учетом (1)
Дальше воспользуемся первоначальным уравнением расстояния, с учетом того, что ускорение , а конечная скорость
равна 0
или с учетом (2)
II способ Запишем закон сохранения энергии при движении бруска вниз по наклонной плоскости
где – конечная скорость тела.
Воспользуемся законом сохранения импульса
Или в проекции на ось, совпадающую с движением тела
где – скорость составного тела сразу после попадания пули.
Отсюда
или же с учетом (1)
Запишем закон сохранения энергии при движении тела вверх по наклонной плоскости
Тогда с учетом (2) равно
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к бруску и пуле модели материальной точки
3. Обосновано применение закона сохранения импульса
4. Обосновано применение закона сохранения энергии
5. Введен нулевой уровень потенциальной энергии
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: закон сохранения механической энергии,
закон сохранения импульса);
II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением
обозначений констант, указанных в варианте КИМ, обозначений величин, используемых в условии
задачи, и стандартных обозначений величин, используемых при написании физических законов);
III) представлены необходимые математические преобразования и расчёты (подстановка числовых
данных в конечную формулу), приводящие к правильному числовому ответу (допускается решение «по
частям» c промежуточными вычислениями);
IV) представлен правильный ответ с указанием единиц измерения искомой величины
2 балла ставится если:
_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности,
и проведены необходимые преобразования, но имеется один или несколько из следующих
недостатков.
Записи, соответствующие пункту II представлены не в полном объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях / вычислениях пропущены логически важные шаги.
И (ИЛИ)
Отсутствует пункт V, или в нём допущена ошибка (в том числе в записи единиц измерения величины)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Представлены только положения и формулы, выражающие физические законы, применение которых
необходимо для решения данной задачи, без каких-либо преобразований с их использованием,
направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решения данной задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла
Ошибка.
Попробуйте повторить позже
В маленький шар, висящий на нити длиной см, попадает и застревает в нём горизонтально летящая со скоростью
м/с пуля массой
г. Определите максимальную массу шара, при которой он после этого совершит полный оборот в
вертикальной плоскости. Сопротивлением воздуха пренебречь. Какие законы Вы используете для решения задачи? Обоснуйте их
применение.
Источники:
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Груз массой имеет малые размеры по сравнению с размерами нити, а пуля еще меньше, поэтому описываем груз и пулю
моделью материальной точки. После соударения систему тел "пуля + шарик"также будем описывать моделью материальной точки.
Относительно ИСО можно записать второй закон Ньютона.
3. Так как изменения механической энергии тела в ИСО равно работе всех непотенциальных сил, приложенных к телу, а в данном случае такой силой является только сила натяжения нити, (сопротивлением воздуха пренебрегаем, трения нет, поверхность гладкая), при этом в любой точке траектории сила натяжения нити перпендикулярна скорости, поэтому работа этой силы равняется нулю и полная механическая энергия системы тел "пуля + шарик"при его движении сохраняется.
4. Так как рассматриваем ИСО, то применим второй закон Ньютона, также применим закон сохранения импульса в горизонтальном направлении, поскольку момент соударения мгновенный и в горизонтальном напарвлении не действуют никакие силы.
5. Система тел "пуля + шарик"движется по окружности и обладает центростремительным ускорением, направленным к центр
окружности вращения. Условием прохождения верхней точки, является натяжение нити. Для того, чтобы нить не провисла, должно
выполняться условие, что сила натяжения больше, либо равна 0. Крайним случаем будет являться , будем рассматривать это
условие.
6. За нулевой уровень потенциальной энергии примем нижнюю точку траектории движения системы тел "пуля + шарик".
Решение
Запишем закон сохранения импульс в момент удара и закон сохранения энергии после удара и до подъема на максимальную высоту
|
|
где – скорость пули и шарика после удара,
– скорость в наивысшей точке,
– масса шарика.
Кроме того, максимальность груза означает, что в наивысшей точке сила натяжения нити обращается в ноль (но только в
наивысшей). Для второго закона Ньютона это выглядит следующим образом
Подставим в закон сохранения энергии и выразим
Из закона сохранения импульса найдем массу шарика
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телам и системе тел после взимодействия модели материальной точки
3. Обосновано применение закона сохранения импульса
4. Обосновано применение второго закона Ньютона
5. Обосновано применение закона сохранения энергии
6. Обосновано наличие центростремительного ускорения
7. Введен нулевой уровень потенциальной энергии
8. Описано условие прохождение верхней точки траектории.
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: закон сохранения импульса, сначала в
векторном виде, после в проекции на выбранные оси. Закон сохранения энергии. Второй закон
Ньютона.).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)
И (ИЛИ)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
И (ИЛИ)
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Ошибка.
Попробуйте повторить позже
На противоположных концах тележки массы M, находящейся на гладкой горизонтальной поверхности, стоят два ученика
одинаковой массы каждый. Длина тележки
. Вначале система неподвижна. Один ученик бросает мяч, а другой ловит. Масса
мяча
. В процессе полета горизонтальная составляющая скорости мяча относительно поверхности, на которой находится
тележка, равна
.
1. Найдите скорость тележки после броска.
2. Найдите продолжительность полета мяча.
3. Найдите скорость тележки после того, как второй ученик поймает мяч.
Силу сопротивления воздуха считайте пренебрежимо малой.
(«Физтех», 2020, 10 )
1. Запишем закон сохранения импульса
2. Так как тележка движется противоположно движению шарика, то
3. Запишем закон сохранения импульса
Ошибка.
Попробуйте повторить позже
Маятник массы вращается в вертикальной плоскости, совершая полный оборот. Найдите разность
максимальной и минимальной сил натяжения нити. Какие законы вы использовали для решения
задачи? Обоснуйте их применение.
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Грузик движется поступательно, его размеры малы по сравнению с размерами установки, будем описывать грузик моделью материальной точки.
3. Применим закон сохранения энергии, так как единственной не потенциальной силой в процессе движения является сила натяжения нити, при этом она направлена перпендикулярно вектору перемещения, а значит её работа равна 0.
4. При вращении грузика, он будет двигаться по окружности и будет обладать центростремительным ускорением, направленным к центру окружности.
5. За нулевой уровень потенциальной энергии примем нижнюю точку траектории движения грузика.
Решение
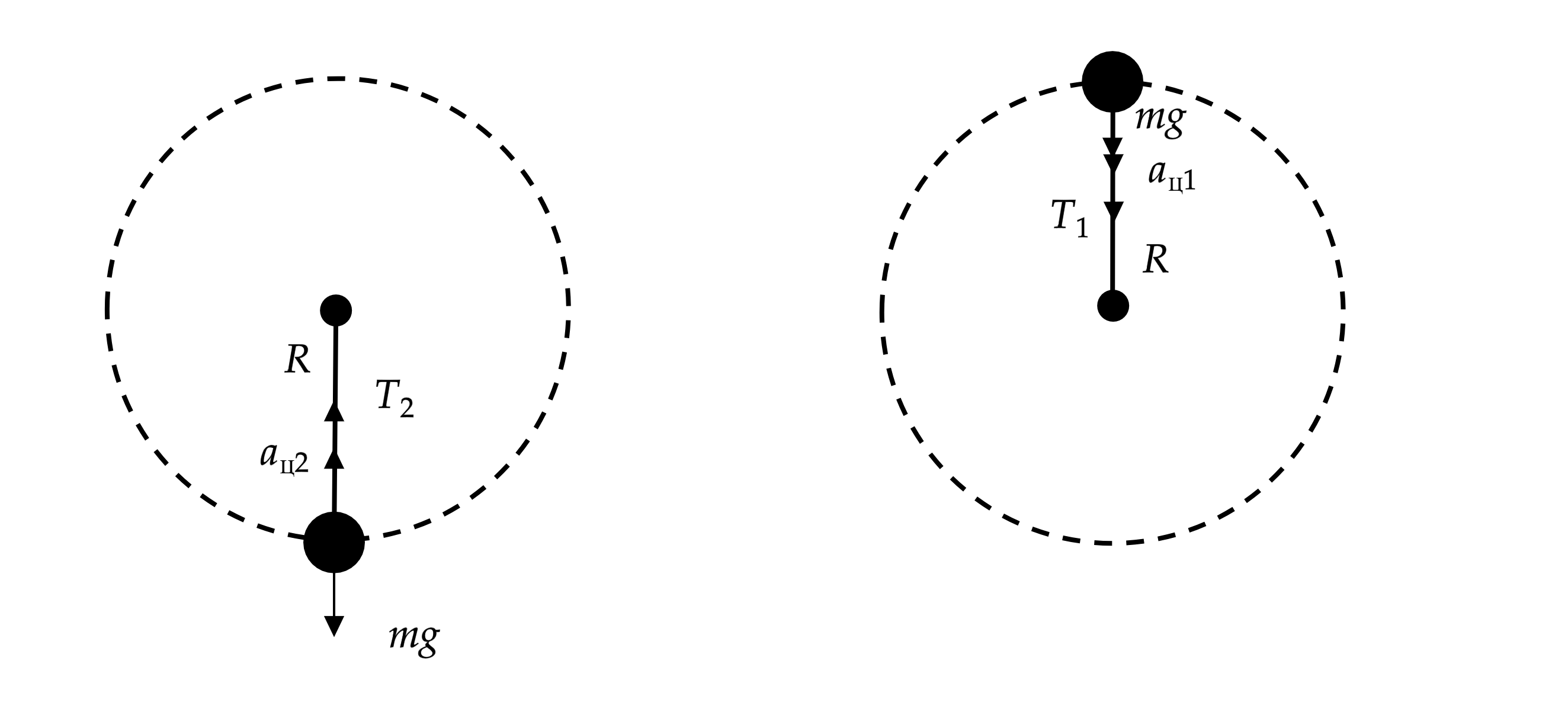
Пусть длина нити , скорость маятника в верхней точке равна
, а в нижней точке
соответственно,
и
– сила
натяжения нити в верхней и нижней точках тогда из закона сохранения энергии
Потенциальную энергию можно рассчитать по формуле , где
- высотана которой находится тело.
Кинетическую энергию можно рассчитать по формуле , где
- скорость с которой движется тело в рассматриваемый момент
вемени.
Запишем второй закон Ньютона:
где – центростремительное ускорение.
Спроецируем второй закон Ньютона на вертикальную ось для двух положений:
|
|
Вычтем из второго уравнения первое, с учетом (1)
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к грузику модели материальной точки
3. Обосновано применение второго закона Ньютона
4. Обосновано применение закона сохранения энергии
5. Введен нулевой уровень потенциальной энергии
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы: I) записаны положения теории и
физические законы, закономерности, применение которых необходимо для решения задачи выбранным
способом (в данном случае: закон сохранения механической энергии, закон сохранения импульса);
II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением
обозначений констант, указанных в варианте КИМ, обозначений величин, используемых в
условии задачи, и стандартных обозначений величин, используемых при написании физических
законов);
III) представлены необходимые математические преобразования и расчёты (подстановка числовых
данных в конечную формулу), приводящие к правильному числовому ответу (допускается решение «по
частям» c промежуточными вычислениями);
IV) представлен правильный ответ с указанием единиц измерения искомой величины
2 балла ставится если:
_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности,
и проведены необходимые преобразования, но имеется один или несколько из следующих
недостатков. Записи, соответствующие пункту II представлены не в полном объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях / вычислениях пропущены логически важные шаги.
И (ИЛИ)
Отсутствует пункт V, или в нём допущена ошибка (в том числе в записи единиц измерения величины)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев. Представлены только положения
и формулы, выражающие физические законы, применение которых необходимо для решения данной
задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решения данной задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла
Ошибка.
Попробуйте повторить позже
Маленький шарик массой проходит мёртвую петлю радиуса
, соскальзывая без начальной скорости с высоты
(см.
рисунок). Трения нет.
а) С какой силой шарик давит на опору в нижней и верхней точках петли, если =
?
б) Найдите минимальную высоту , необходимую для прохождения петли.
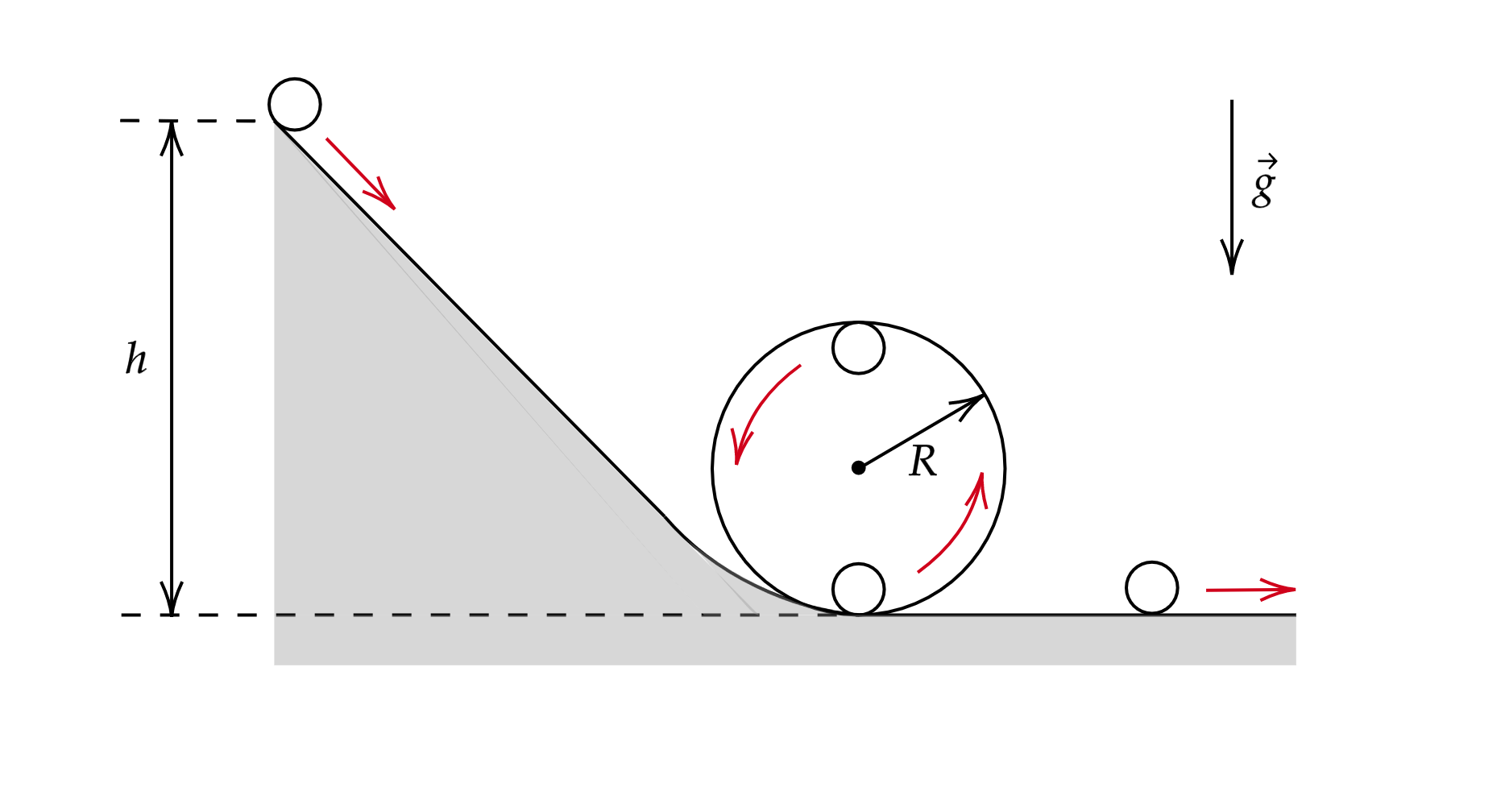
Сделаем рисунок сил
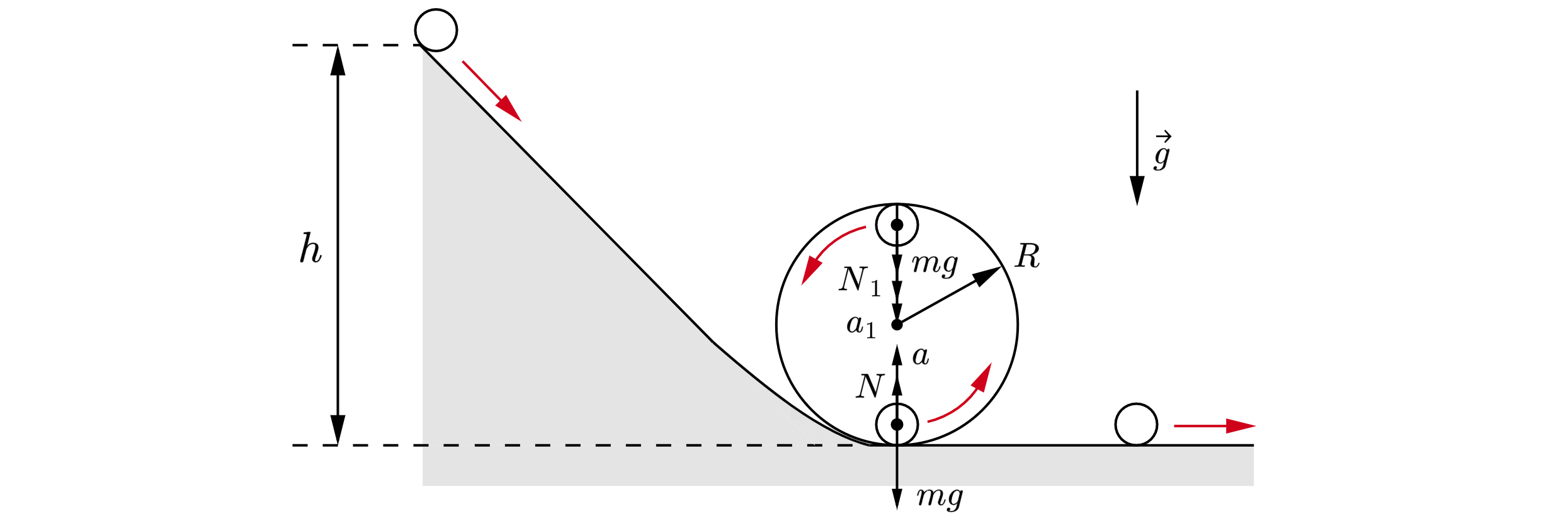
Где и
– сила реакции опоры в нижней и верхней точке,
и
– центростремительное ускорение в нижней и верхней
точке,
– сила тяжести.
1. Найдем скорость тела в нижней точке движения по закону сохранения энергии
Запишем второй закон Ньютона:
Спроецируем второй закон Ньютона на вертикальную ось:
Сила давления на петлю равна по модулю и обратна по направлению силе реакции опоры, следовательно, сила давления внизу
равна Скорость тела в верхней точке также можно найти из закона сохранения энергии
Тогда второй закон Ньютона запишется в следующей виде
2. Для того, чтобы тело прошло петлю, необходимо, чтобы сила реакции опоры во время прохождения ни разу не была равна 0,
минимальная сила реакции опоры наблюдается в верхней точке движения. Докажем это
Пусть угол между силой тяжести и силой реакции опоры равен , тогда второй закон в проекции на ось, направленную в центр
окружности:
Тогда из закона сохранения энергии
Тогда второй закон Ньютона запишется в виде
Тогда, для того, чтобы было минимально,
должен быть максимален, значит
, что возможно только в верхней
точке.
Из закона сохранения энергии скорость в верхней точке
Примем в верхней точке силу реакции опоры равно 0, тогда
Ошибка.
Попробуйте повторить позже
Горка массой с покоящейся на её вершине шайбой массой m скользит со скоростью
по гладкой горизонтальной
поверхности стола в направлении покоящейся незакреплённой горки массой
(см. рисунок). От незначительного
толчка шайба съезжает с горки, горка останавливается, а шайба движется по столу в направлении горки массой
.
1) Найдите высоту горки массой .
2) На какую максимальную высоту сможет подняться шайба на горке массой ?
Поверхности горок гладкие. Горки имеют плавный переход к поверхности стола. Шайба не отрывается от поверхности горок, а
поступательно движущиеся горки — от стола. Направления всех движений находятся в одной вертикальной плоскости.
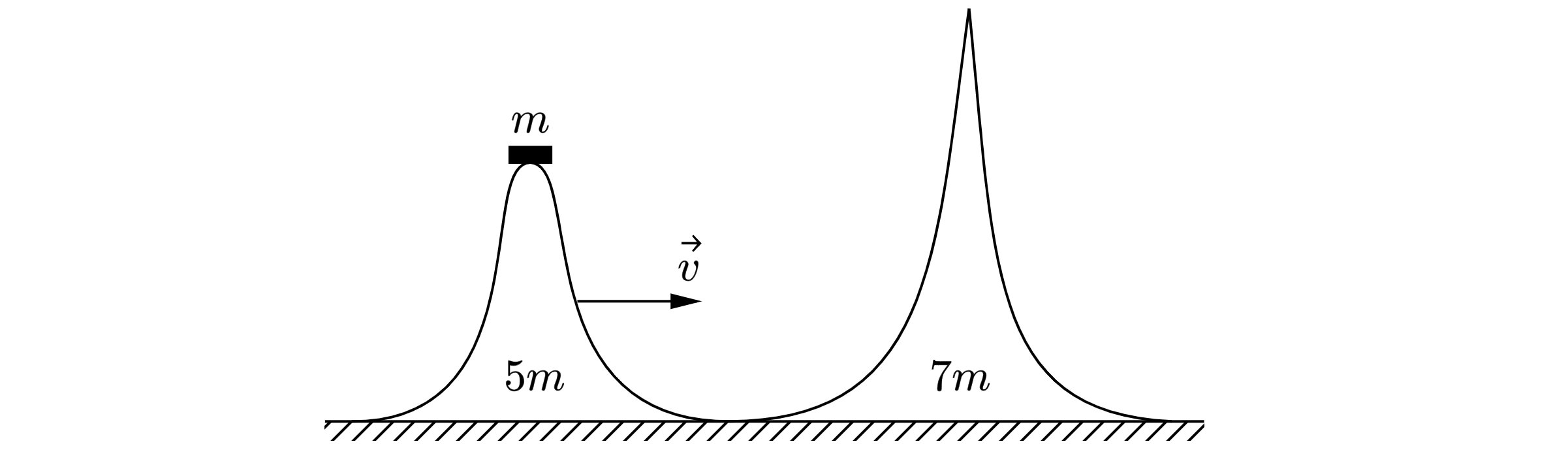
1) Запишем закон сохранения импульса при движении шайбы вниз с первой горки:
где – скорость горки массой
после скатывания горки,
– скорость шайбы внизу горки.
Спроецируем закон сохранения импульса на горизонтальную ось, с учётом, что по условию :
отсюда
Запишем закон сохранения энергии при движении шайбы вниз:
где – высота горки.
Тогда
2) Шайба перестанет подниматься на горку в момент, когда их скорости станут равны, пусть эта скорость равна . Запишем
закон сохранения импульса:
спроецируем на горизонтальную ось и подставим :
Запишем закон сохранения энергии при движении шайбы вверх по горке массой :
где – искомая высота.
С учётом и
имеем
Ошибка.
Попробуйте повторить позже
Два шарика, массы которых соответственно г и
г, висят, соприкасаясь, на одинаковых вертикальных
нитях длиной
см. Первый шар отклонили на угол
и отпустили. На какую высоту поднимутся шарики
после удара, если этот удар абсолютно неупругий? Обоснуйте применимость законов, используемых для решения
задачи.
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Движение тел является поступательным, а значит их можно считать материальными точками.
3. Так как грузы являются материальными точками и удар неупругий, описывать это будем при помощи закона сохранения импульса.
4. При движении тел силы натяжения нити направлены перпендикулярно вектору перемещения, а значит работа этих сил равна нулю, значит, полная механическая энергий тел остается неизменной и выполняется закон сохранения механической энергии.
Решение
Запишем закон сохранения энергии при движении первого шарика
где – скорость первого шарика перед столкновением.
Запишем закон сохранения импульса:
где – скорость шариков после соударения.
Спроецируем на горизонтальную ось:
Также запишем закон сохранения энергии после соударения:
где – искомая величина.
Из первого уравнения находим :
подставляем во второе и находим :
Подставляем в третье и выражаем :
Ошибка.
Попробуйте повторить позже
Два шарика подвешены на вертикальных тонких нитях так, что они находятся на одной высоте. Между шариками
находится сжатая и связанная нитью лёгкая пружина. При пережигании связывающей нити пружина распрямляется,
расталкивает шарики и падает вниз. В результате нити отклоняются в разные стороны на одинаковые углы. Во сколько
раз одна нить длиннее другой, если отношение масс шариков ? Считать величину сжатия пружины
во много раз меньше длин нитей. Какие законы Вы используете для решения задачи? Обоснуйте их применение.
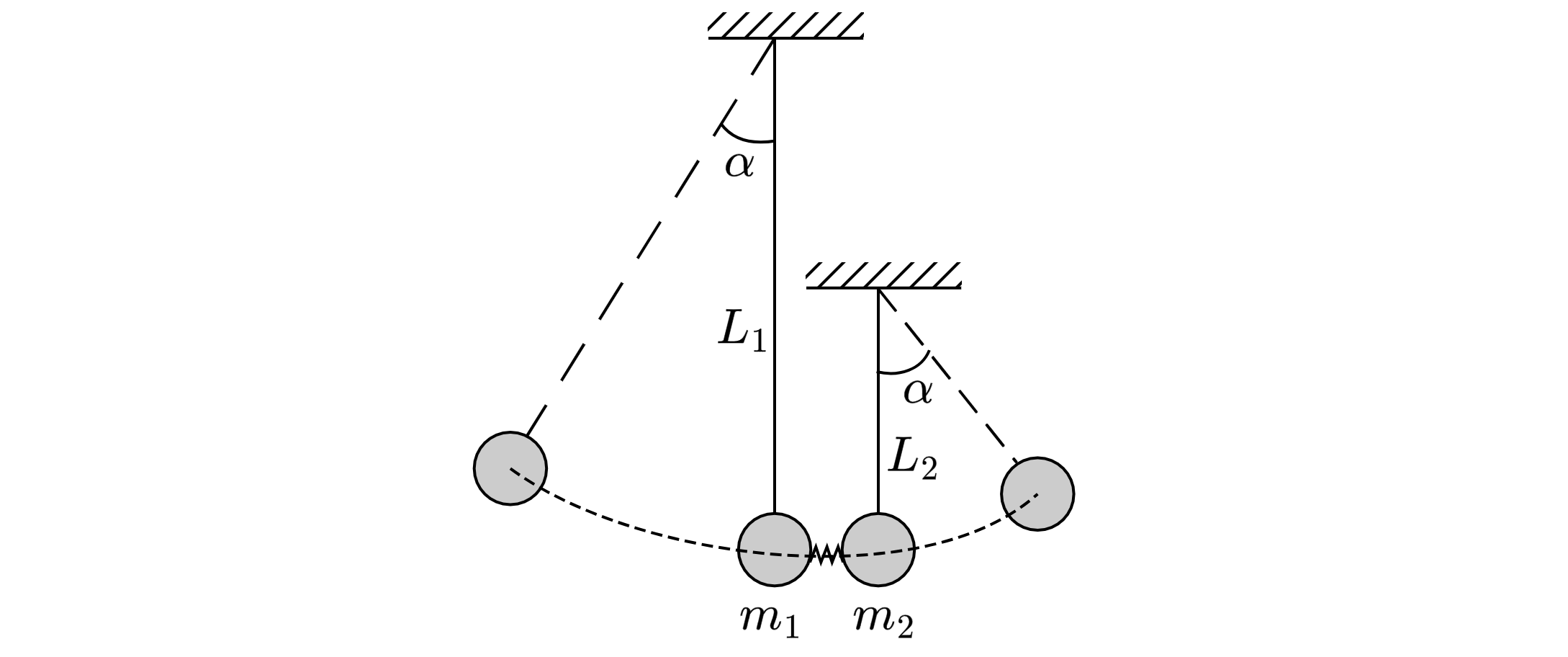
Обоснование
1. Введем инерциальную систему отсчёта (ИСО), связанную с землей.
2. Тела движутся поступательно, их размеры малы по сравнению с размерами установки, будем описывать тела моделью
материальной точки.
3. При пережигании нити пружина толкает оба шарика, действуя на шарики внутренней силой — силой упругости, все внешние
силы, действующие на систему двух шариков, направлены вертикально (силы тяжести и натяжения нитей), поэтому сохраняется
горизонтальная проекция импульса системы шариков, поскольку импульс пружины пренебрежимо мал из-за её малой
массы.
В процессе движения каждого шарика на нити к верхней точке своей траектории на каждый из них действуют сила тяжести и
сила натяжения нити
Изменение механической энергии шарика в ИСО равно работе всех непотенциальных сил, приложенных к
нему. В данном случае единственной такой силой является сила натяжения нити
В каждой точке траектории, она приложена
перпендикулярно вектору скорости
поэтому работа силы
равна нулю, а механическая энергия каждого шарика на этом
участке его движения сохраняется.
4. За нулевой уровень потенциальной энергии примем уровень, когда тела сцеплены пружиной и находятся на одном
уровне.
Решение
Высота равна
тогда
Потенциальная энергия тела на высоте равна
где – масса тела.
Кинетическая энергия
– скорость тела.
По закону сохранения импульса
А по закону сохранения энергии
Сократив массы с двух сторон уравнений, получим
Разделив первое уравнение на второе и, учитывая, что , получим
Откуда
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телам модели материальной точки
3. Обосновано применение закона сохранения импульса
4. Обосновано применение закона сохранения энергии
5. Введен нулевой уровень потенциальной энергии
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: закон сохранения импульса, закон
сохранения энергии, формула импульса, формула кинетической энергии, формула потенциальной
энергии).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)
И (ИЛИ)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
И (ИЛИ)
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Ошибка.
Попробуйте повторить позже
Шар массой 1 кг, подвешенный на нити длиной 90 см, отводят от положения равновесия на угол и отпускают. В момент
прохождения шаром положения равновесия в него попадает пуля массой 10 г, летящая навстречу шару. Она пробивает его и
продолжает двигаться горизонтально. Определите изменение скорости пули в результате попадания в шар, если он, продолжая
движение в прежнем направлении, отклоняется на угол
. (Массу шара считать неизменной, диаметр шара – пренебрежимо
малым по сравнению с длиной нити,
.) Какие законы Вы используете для решения задачи? Обоснуйте их
применение.
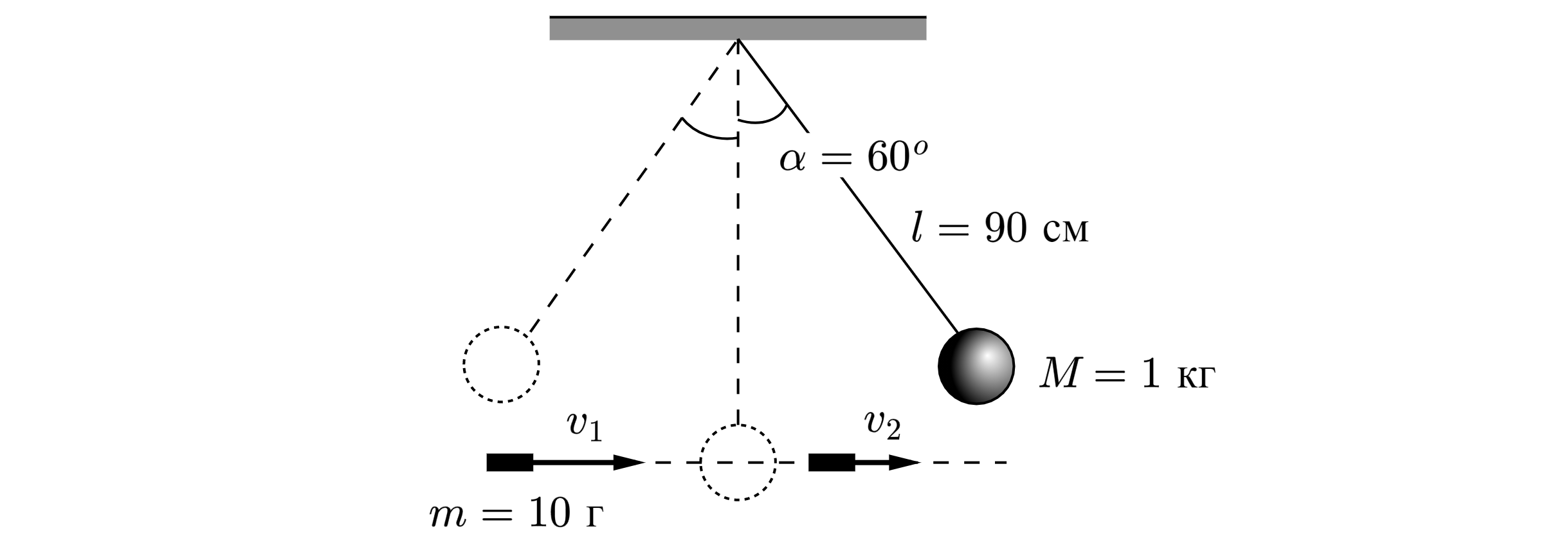
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тела движутся поступательно, размеры шарика малы по сравнению с размерами нити, а пуля еще меньше, поэтому будем описывать шарик и пулю моделью материальной точки.
3. Будем считать, что время соударения шарика и пули мало, а значит нить за это время не успевает заметно отклониться,
поэтому в момент столкновения все силы направлены вертикально. Следовательно, в ИСО при попадании пули в шарик сохраняется
горизонтальная составляющая импульса системы тел "шарик + пуля
".
4. После попадания пули в шарик при движении тел по вертикальной окружности механическая энергия равна сумме кинетической и потенциальной энергии тел. То есть
Так как изменения механической энергии тела в ИСО равно работе всех непотенциальных сил, приложенных к телу, а в данном
случае такой силой является только сила натяжения нити (сопротивлением воздуха пренебрегаем), при этом в любой точке
траектории сила натяжения нити перпендикулярна скорости, поэтому работа силы натяжения нити
равняется
нулю.
5. За нулевой уровень потенциальной энергии примем уровень положения равновесия шара.
Решение
Потенциальная энергия на высоте равна
где – высота подъема,
– масса тела,
– длина нити,
– угол отклонения нити.
Кинетическая энергия в нижней точке
где – скорость шара в нижней точке.
Запишем закон сохранения энергия для движения шарика вниз
Запишем закон сохранения импульс в момент удара и закон сохранения энергии после удара и до подъема на максимальную высоту
|
|
где – высота подъема,
– масса пули,
– скорости шара после столкновения.
Тогда
Искомая величина равна:
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телам модели материальной точки
3. Указано, что время прохождения пули через шарик мало, и за это время нить вместе с шариком не изменяет своего положения
4. Обосновано применение закона сохранения энергии
5. Сказано, что работа силы натяжения нити при движении шарика равна нулю, так как в любой момент времени она перпендикулярна траектории движения шарика
6. Введен нулевой уровень потенциальной энергии
7. Сказано, что при прохождении пули через шарик на нее действуют силы трения, поэтому удар следует рассматривать как не упругий
8. Обосновано применение закона сохранения импульса
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
Приведено полное правильное решение, включающее следующие элементы:
1) верно записаны формулы, выражающие физические законы, применение которых необходимо для
решения задачи выбранным способом (в данном решении — закон сохранения импульса и закон
сохранения энергии);
2) проведены необходимые математические преобразования и расчеты, приводящие к правильному
числовому ответу, и представлен ответ. При этом допускается решение "по частям"(с промежуточными
вычислениями).
2 балла ставится если:
_________________________________________________________________________________________________________________
— Представлено правильное решение только в общем виде, без каких-либо числовых расчетов.
ИЛИ
— Правильно записаны необходимые формулы, записан правильный ответ, но не представлены преобразования, приводящие к ответу.
ИЛИ
— В математических преобразованиях или вычислениях допущена ошибка, которая привела к неверному ответу.
1 балл ставится если:
_________________________________________________________________________________________________________________
— В решении содержится ошибка в необходимых математических преобразованиях, и отсутствуют
какие-либо числовые расчеты.
ИЛИ
— Записаны и использованы не все исходные формулы, необходимые для решения задачи, или в ОДНОЙ из них допущена ошибка
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла (использование неприменимого закона, отсутствие более одного исходного уравнения, разрозненные записи и т.п.).
Ошибка.
Попробуйте повторить позже
От груза, неподвижно висящего на невесомой пружине жёсткостью = 400 Н/м, отделился с начальной скоростью, равной нулю,
его фрагмент. После этого при возникших колебаниях оставшаяся часть груза поднималась на максимальную высоту
= 3 см
относительно первоначального положения. Какова масса m отделившегося от груза фрагмента? Какие законы Вы использовали для
описания движения? Обоснуйте их применение к данному случаю.

Источники:
Обоснование
1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.
2. Кубик массой и
имеет малые размеры по сравнению с пружиной и движутся поступательно, поэтому описываем
кубики моделью материальной точки. Так как тела являются материальными точками, то описывать их движение в ИСО будем с
помощью второго закона Ньютона
3. Так как изменения механической энергии тела в ИСО равно работе всех непотенциальных сил, приложенных к телу, а в данном случае таких сил нет, (сопротивлением воздуха пренебрегаем, трения нет) полная механическая энергия кубика при его движении сохраняется.
4. Так как деформации упругие, то применим закон Гука для нахождения силы упругости, действующей на тело во время возникших колебаний.
Решение
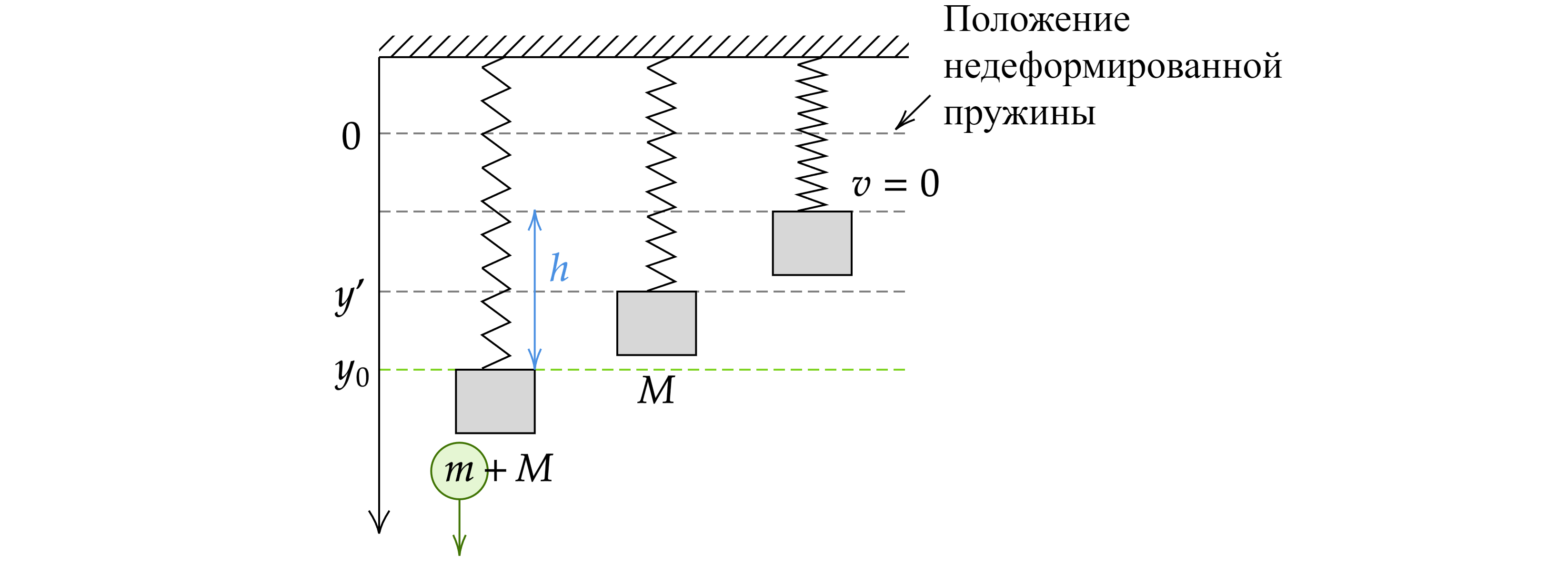
В начальном положении тело находилось в равновесии, то есть сила тяжести уравновешивает силу Гука
где – сила Гука. Или в проекции на ось
Так как начальная скорость куска равна нулю, то и скорость
после отделения также равна нулю. После отделения части
груза, будут совершаться гармонические колебания, значит по закону сохранения энергии
Раскроем скобки
Отсюда
| Критерии оценивания выполнения задачи | Баллы |
| Критерий 1 | |
| Верно обоснована возможность испольования законов | 1 |
| (закономерностей). В данном случае: выбор ИСО, модель материальной точки, использование закона Гука, использование второго закона Ньютона, использование закона сохранения энергии | |
| В обосновании возможности использования законов | 0 |
| (закономерностей) допущена ошибка | |
|
ИЛИ
| |
| Обоснование отсутствует | |
| Критерий 2 | |
| Приведено полное решение, включающее следующие элементы: | 3 |
| I) записаны положения теории и физические законы, | |
| закономерности, применение которых необходимо для решения | |
| задачи выбранным способом (в данном случае - закон Гука, второй закон Ньютона, закон сохранения механической энергии, формула потенциальной энергии упруго деформированного тела); | |
| II) описаны вновь вводимые в решении буквенные обозначения | |
| физических величин (за исключением обозначений констант, | |
| указанных в варианте КИМ, обозначений величин, используемых | |
| в условии задачи, и стандартных обозначений величин, | |
| используемых при написании физических законов); | |
| III) проведены необходимые математические преобразования | |
| и расчёты (подстановка числовых данных в конечную формулу), | |
| приводящие к правильному числовому ответу (допускается решение | |
| «по частям» с промежуточными вычислениями); | |
| IV) представлен правильный ответ с указанием единиц измерения | |
| фиизческой величины | |
| Правильно записаны все необходимые положения теории, | 2 |
| фиизческие законы, закономерности, и проведены необходимые | |
| преобразования, но имеется один или несколько из следующих | |
| недостатков. | |
|
| |
| Записи, соответствующие пункту II, представлены не в полном | |
| объёме или отсутствуют. | |
|
И(ИЛИ)
| |
| В решении имеются лишние записы, не входящие в решение | |
| (возможно, неверные), которые не отделены от решения и не | |
| зачёркнуты | |
|
И(ИЛИ)
| |
| В необходимых математических преобразованиях или вычислениях | |
| допущены ошибки, и(или) в математических преобразованиях/ | |
| вычислениях пропущены логически важные шаги. | |
|
И(ИЛИ)
| |
| Отсутствует пункт IV, или в нём допущена ошибка (в том числе | |
| в записи единиц измерений величины) | |
| Представлены записи, соответствующие одному из следующих | 1 |
| случаев. | |
| Представлены только положения и формулы, выражающие | |
| физические законы, применение которых необходимо для решения | |
| данной задачи, без каких-либо преобразований с их | |
| использованием, направленных на решение задачи. | |
|
ИЛИ
| |
| В решении отсутствует ОДНА из исходных формул, необходимая | |
| для решения данной задачи (или утверждение, лежащее в основе | |
| решения), но присутствуют логически верные преобразования | |
| с имеющимися формулами, направленные на решение задачи. | |
|
ИЛИ
| |
| В ОДНОЙ из исходных формул, необходимых для решения данной | |
| задачи (или в утверждения, лежащем в основе решения), допущена | |
| ошибка, но присутствуют логически верные преобразования | |
| с имеющимися формулами, направленные на решение задачи | |
| Все случаи решения, которые не соответствуют вышеуказанным | 0 |
| критериям выставления оценок в 1, 2, 3 балла | |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Система из грузов и
связывающей их лёгкой нерастяжимой нити в начальный момент покоится вертикальной плоскости,
проходящей перпендикулярно оси О закреплённой сферы. Груз
находится в точке
на вершине сферы (см. рисунок). В ходе
возникшего движения груз отрывается от поверхности сферы, пройдя по ней дугу
. Найдите массу
, если
кг.
Размеры груза
ничтожно малы по сравнению с радиусом сферы. Трением пренебречь. Сделайте схематический
рисунок с указанием сил, действующих на грузы. Какие законы Вы используете для решения задачи? Обоснуйте их
применение.
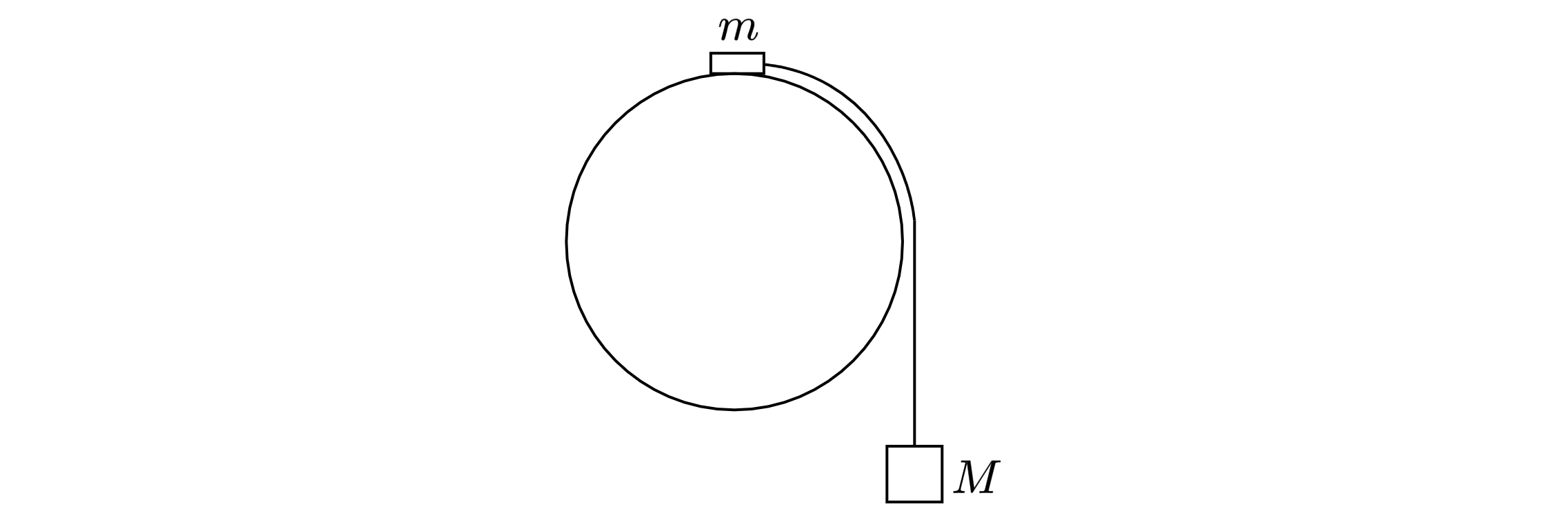
Основная волна 2012
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тела движутся поступательно, их размеры малы по сравнению с размерами установки, будем описывать тела моделью материальной точки.
3. Используя пункты 1 и 2 описывать момент отрыва будем использовать второй закон Ньютона относительно ИСО.
4. Так как нить легкая и трение отсутствует, натяжение нити в любой ее точке одинаково. Так как нить нерастяжимая то тела будут двигаться с одинаковыми скоростями.
5. В процессе движения на грузы действуют непотенциальные силы - сила реакции опоры и силы натяжения
нити. Сила реакции опоры перпендикулярна скорости, поэтому её работа равняется нулю. Силы натяжения нити
действующая на груз сонаправлена с ее скоростью, сила натяжения нити действующая на груз
направлена
против ее скорости. Значит, суммарная работа двух этих сил равняется нулю, следовательно выполняется закон
сохранения энергии для системы тел. (Нить - является идеальной связью, суммарная работ ее в системе равняется
нулю).
6. Так как груз будет двигаться по окружности, то он будет обладать центростремительнм ускорением, направленным к
центру окружности вращения.
7. За нулевой уровень потенциальной энергии примем уровень центра сферы.
Решение
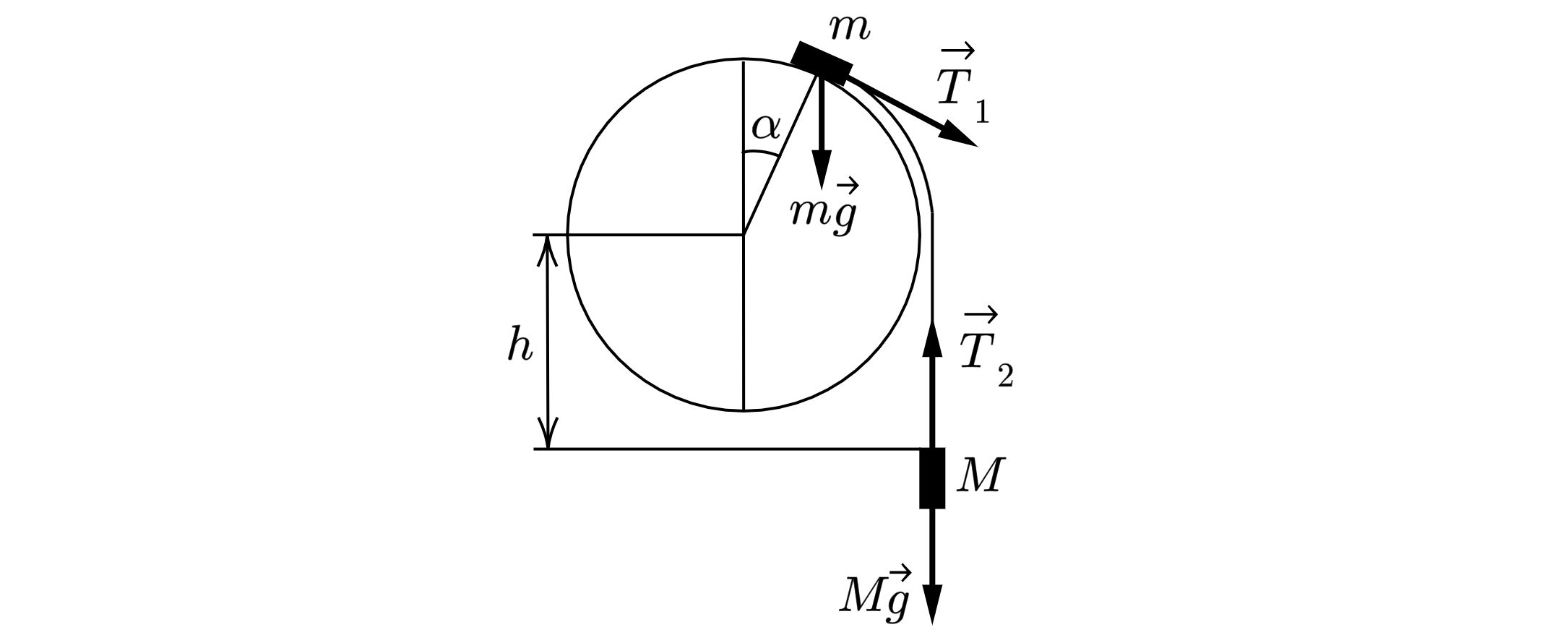
Найдем модуль скорости груза в точке отрыва его от поверхности сферы. Для этого приравняем друг другу значения
механической энергии системы грузов в начальном состоянии и в состоянии, когда груз m находится в точке отрыва (потенциальную
энергию грузов в поле тяжести отсчитываем от уровня центра сферы, в начальном состоянии груз
находится ниже центра
сферы на величину
):
где – радиус трубы,
. Отсюда
Груз в точке отрыва еще движется по окружности радиусом
, но уже не давит на сферу. Поэтому его
центростремительное ускорение вызвано только силой тяжести, так как сила
направлена по касательной к сфере (см.
рисунок):
Подставляя сюда значение , получим:
Отсюда:
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телам модели материальной точки
3. Обосновано применение второго закона Ньютона для, сказано, что в момент отрыва сила реакции опоры обращается в ноль
4. Обосновано применение закона сохранения энергии
5. Обосновано равенство скоростей грузов
6. Введен нулевой уровень потенциальной энергии
7. Обосновано равенство натяжения нитей
8. Обосновано наличие центростремительного ускорения
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) записаны положения теории и физические законы, закономерности; применение которых необходимо
для решения задачи выбранным способом (в данном случае: закон сохранения механической энергии,
формула для величины центростремительного ускорения);
II) описаны все вводимые в решении буквенные обозначения физических величин (за исключением
обозначений констант, указанных в варианте КИМ, и обозначений, используемых в условии задачи);
III) представлен схематический рисунок с указанием сил, поясняющий решение;
IV) проведены необходимые математические преобразования (допускается вербальное указание на их
проведение) и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям»
с промежуточными вычислениями);
V) представлен правильный ответ с указанием единиц измерения искомой величины
2 балла ставится если:
_________________________________________________________________________________________________________________
Правильно записаны необходимые положения теории и физические законы, закономерности; проведены
необходимые преобразования, и представлен правильный ответ с указанием единиц измерения искомой
величины. Но имеется один из следующих недостатков. Записи, соответствующие одному
или нескольким пунктам: II, III, IV, – представлены не в полном объёме или отсутствуют
И (ИЛИ)
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)
ИЛИ
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
ИЛИ
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) преобразования/вычисления не доведены до конца.
ИЛИ
При ПОЛНОМ решении отсутствует пункт V, или в нём допущена ошибка 1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Представлены только положения и формулы, выражающие физические законы, применение которых
необходимо для решения задачи, без каких-либо преобразований с их использованием, направленных на
решение задачи, и ответа.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решения задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла
Ошибка.
Попробуйте повторить позже
На горизонтальном гладком столе лежит длинная доска массой а на её левом конце – деревянный брусок массой
(см. рисунок). В брусок попадает и прилипает к нему пластилиновый снаряд массой
летевший
горизонтально по направлению вдоль доски со скоростью
после чего брусок скользит до остановки по шероховатой
доске, не сваливаясь с неё. Какая часть начальной кинетической энергии «пули» перейдёт в этой системе в теплоту в течение всего
процесса? Выразите в процентах. Какие законы Вы используете для решения задачи? Обоснуйте их применение.

Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Пуля и брусок движутся поступательно, их размеры малы по сравнению с размерами установки, будем описывать их моделью материальной точки.
3. Система «доска-брусок-пуля» является замкнутой, т.к. плоскость гладкая, сила трения не действует. Сила реакции опоры и сила тяжести направлены по вертикали, поэтому не оказывают влияния на горизонтальную скорость. В инерциальной системе отсчета применим закон сохранения импульса при абсолютно неупругом ударе.
4. При абсолютно неупругом ударе в инерциальной системе отсчета применим закон превращения энергии.
Решение
1) Остановка бруска с пулей относительно доски произойдет в момент равенства их скоростей относительно стола. Запишем закон сохранения импульса для системы "брусок + пуля + доска":
где – скорость движения доски (системы) относительно стола после остановки бруска.
Спроецируем закон сохранения импульса на горизонтальную ось:
Таким образом равна
2) В начальном состоянии механическая энергия системы равна только кинетической энергии пули а в
конечном – кинетической энергии всей системы
3) Разность кинетических энергий и будет искомое количество теплоты:
4) Найдем какая часть начальной кинетической энергии «пули» перейдёт в этой системе в теплоту
Т.е. 96.
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телу модели материальной точки
3. Обосновано применение закона сохранения импульса
4. Обосновано применение закона сохранения энергии
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: формула импульса, закон сохранения
импульса в векторном виде и в проекции на координатную ось, закон превращения энергии, формула
кинетической энергии).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)
И (ИЛИ)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
И (ИЛИ)
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Ошибка.
Попробуйте повторить позже
На горизонтальном шероховатом столе лежит брусок массой кг, соединённый через систему идеальных блоков невесомой и
нерастяжимой нитью с грузом массой
кг, висящим на высоте
м над столом (см. рисунок). Груз начинает движение
без начальной скорости и абсолютно неупруго ударяется о стол. Какое количество теплоты
выделяется при этом ударе?
Коэффициент трения бруска о стол равен
. Какие законы Вы используете для решения задачи? Обоснуйте их
применение.

Обоснование
1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.
2. Размеры тел небольшие по сравнению с размерами установки, будем описывать их моделью материальной точки.
3. Так как тела являются материальными точками, то для описания их движения будем использовать второй закон Ньютона относительно ИСО.
4. При абсолютно неупругом ударе вся энергия перейдет в тепловую.
5. Так как нить невесома, то силы натяжения нитей, действующие на грузы равны между собой. Так как нить нерастяжима, то можно утверждать, что тела движутся с одинаковыми по модулю ускорениями
Решение
Расставим силы, действующие на бруски.

Где – сила реакции столы,
– сила натяжения нити,
– сила трения,
– ускорения брусков. Ускорения брусков
равны, так как нить нерастяжима.
Запишем второй закон Ньютона для каждого из брусков:
Спроецируем вторые законы Ньютона на оси и
|
|
Сила трения же равна
Сложение первых двух уравнений дает:
При абсолютно неупругом ударе вся кинетическая энергия второго груза выделится в виде тепла
где – скорость груза перед соударением.
Запишем уравнение кинематики на вертикальную ось
где – начальная скорость,
– проекция ускорения.
Вертикальная проекция скорости изменяется по закону:
Тогда в момент падения на землю:
Тогда
И искомая величина:
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к грузам модели материальной точки
3. Обосновано применение второго закона Ньютона для описания движения грузов
4. Обосновано постоянство силы натяжения нити в любом ее сечении и равенство ускорений движения грузов
5. Сказано как находится количество теплоты в случае абсолютно не упругого удара тел
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: закон сохранения и превращения энергии,
второй закон Ньютона в векторной форме и в проекциях на координатные оси, формулы силы трения
скольжения, кинетической энергии точки, формулы для расчета скорости и координаты при
равноускоренном движении тела).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)
И (ИЛИ)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
И (ИЛИ)
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.



