Тема Окружности

Вписанные углы и счёт углов в окружности

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела окружности

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#80740

В выпуклом четырёхугольнике $ABCD$ выполнено $AB = BC = CD$ . Его диагонали $AC$ и $BD$ пересекаются в точке $E$ . Описанная окружность треугольника $ADE$ пересекает сторону $AB$ в точке $P ⁄= A$ и продолжение стороны $CD$ в точке $Q⁄= D$ . Найдите отношение отрезков $AP$ и $DQ$ .

Источники: Высшая проба - 2024, 11.3 (см. olymp.hse.ru)

Подсказки к задаче

Подсказка 1

Заметьте, что AP и QD – хорды окружности, описанной около треугольника AED. Значит, чтобы доказать, что они равны, нам требуется доказать, что на данные хорды опираются равные вписанные углы. То есть если мы докажем, что углы QAD и ADP равны, то решим задачу. Подумайте, при каком условии данные углы могут быть равны.

Подсказка 2

Обратите внимание, что углы QAD и ADP – накрест лежащие для прямых PD и AQ, а значит, если мы докажем параллельность данных прямых, то решим задачу.

Подсказка 3

В условии не просто так нам дали, что три стороны четырехугольника попарно равны. Давайте рассмотрим равнобедренные треугольники ABC и BCD, а конкретно, рассмотрим их равные углы при основаниях. Подумайте, как они могут помочь в доказательстве параллельности прямых PD и AQ.

Подсказка 4

Рассмотрим два соответственных угла AQD и PDC. Из вписанности четырехугольника AQDE следует равенство ∠AQD = ∠DEC. Обратите внимание, что DEC является внешним углом треугольника BCE, значит, он равен сумме углов EBC и ECB. Вспомним про равнобедренные треугольники: в них есть два равных угла ∠EBC = ∠BDC. Значит, для решения задачи остается доказать, что ∠PDB = ∠ECB. Подумайте, как в этом может помочь окружность.

Подсказка 5

Четырехугольник APDQ является вписанным, значит, углы PAE и PDE будут равными, а угол PAE будет равен углу BCA, так как это углы при основании равнобедренного треугольника.

Показать доказательство

Первое решение.

Из вписанности четырехугольника $APED$ следует, $∠P AE = ∠EDP$ . Треугольник $ABC$ является равнобедренным, а значит $∠BAC =∠BCA$ , следовательно, $∠BCA = ∠BDP$ .

Из равнобедренности треугольника следует, что $∠DBC = ∠CDB$ .

$PIC$

Наконец, в силу вписанности четырехугольника $AEDQ$

∠PDC = ∠PDB + ∠BDC = ∠BCE + ∠DBC = ∠CED =∠AQD

Второе решение.

Достаточно показать, что хорды $AP$ и $QD$ стягивают равные дуги в окружности $(AED )$ , то есть доказать равенство $∠P EA =∠QED$ . По теореме о внешнем угле верно, $∠P EA =∠BP E − ∠P AE.$

Поскольку треугольник $ABC$ является равнобедренным $∠BAE = ∠BCE$ , а из вписанности четырехугольника $AP ED$ следует, что $∠BP E =∠EDA$ . Таким образом,

∠PEA = ∠BP E− ∠PAE = ∠EDA − ∠BCE

Аналогично,

∠DEQ = ∠DAE − ∠EBC

$PIC$

Наконец, исходное равенство углов можно переписать в виде

∠EDA − ∠BCE = ∠DAE − ∠EBC

∠EDA +∠EBC =∠DAE +∠BCE,

что верно, так как суммой углов в каждой части равна углу между диагоналями четырехугольника.

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#80747

Биссектриса угла $A$ параллелограмма $ABCD$ пересекает сторону $BC$ и продолжение стороны $DC$ за точку $C$ в точках $K$ и $M$ соответственно, как показано на рисунке:

$PIC$

Доказать, что центр описанной окружности треугольника $KCM$ лежит на описанной окружности треугольника $BCD$ .

Источники: Всесиб-2024, 11.4 (см. sesc.nsu.ru)

Подсказки к задаче

Подсказка 1

Когда в параллелограмме проведена биссектриса, так и хочется поискать равнобедренные треугольники. Видно, что △KCM — равнобедренный. С чем тогда хочется соединить центр О описанной окружности △KCM?

Подсказка 2

Верно, с точкой C! Тогда OC будет серединным перпендикуляром к KM. Но ведь не любая точка на нём будет центром окружности, поэтому надо как-то еще попользоваться ей. Предлагаю отметить, что OK=OC. А как нам подобраться к описанной окружности △BCD?

Подсказка 3

Можно попытаться доказать, что уголочки ∠OBC и ∠ODC равны. Какие у нас есть для этого инструменты? В самом удачном случае мы просто найдем равные треугольнички... У нас уже есть равенство отрезков OK и OC, поэтому можно попытаться установить равенство △BOK и △DOC...

Подсказка 4

Равенство сторон BK и DC следует из равнобедренности △ABK. Осталось лишь показать, что уголки ∠BKO и ∠DCO равны. Посмотрите на смежные им уголки и завершите решение!

Показать доказательство

Так как $AK$ — биссектриса, то $∠BAK = ∠DAK = α$ . В силу параллельности $BC ||AD$ и $AB ||CD$ также $∠BKA =∠KMC = α$ .

Пусть $O$ — центр окружности, описанной около $MCK$ . Тогда $OC ⊥ KM$ , так как $MCK$ — равнобедренный треугольник. Откуда $∘ ∠MCO = ∠KCO = 90 − α$ .

$PIC$

Также равнобедренными будут треугольники $KOC$ ( $KO =OC$ как радиусы) и $ABK$ (углы $∠BAK$ и $∠BKA$ равны по вышесказанному). Значит,

∠BKO = 180∘ − ∠OKC = 180∘− ∠MCO =∠OCD

Тогда $△BKO = △DCO$ по двум сторонам и углу между ними, потому что $BK =AB = CD$ , радиусы $OK =OC$ , а углы $∠BKO = ∠OCB.$

Следовательно, $∠OBC = ∠ODC$ и тогда точки $O,B,C,D$ лежат на одной окружности.

Ошибка.
Попробуйте повторить позже

Задача 3#83235

В остроугольном треугольнике $ABC$ проведены биссектриса $BL$ и высота $BK.$ Прямые $BL$ и $BK$ пересекают вторично описанную окружность треугольника $ABC$ в точках $W$ и $T$ соответственно. Оказалось, что $BC = BW.$ Докажите, что $TL ⊥ BC.$

Источники: КМО - 2024, вторая задача второго дня для 10-11 классов, автор Шурыгин В.Е. (cmo.adygmath.ru)

Показать доказательство

Из вписанности $∠BAL =∠BAC =∠BW C$ . Получается, что в треугольниках $BAL$ и $BW C$ равны две пары соответствующих углов, значит, равные углы и в третьей паре: $∠BLA = ∠BCW$ . Но из условия $BC = BW$ следует $∠BW C = ∠BCW$ , отсюда $∠BAL = ∠BLA.$

$PIC$

Получается, что треугольник $BAL$ равнобедренный $(BA = BL )$ , тогда $BT$ — его ось симметрии. Значит, $∠BTL =∠BT A$ . Но $∠BT A= ∠BCA =90∘− ∠CBK$ . Видим, что $∠BTL = 90∘− ∠CBT$ , откуда $TL⊥ BC.$

Замечание.

После установления симметрии треугольника $BAL$ относительно $BT$ , можно завершить решение разными способами. Например, заметив, что

∠TCW + ∠CW B =∠T BW + ∠CAB = ∠TBA +∠CAB = 90∘.

Тогда $CT ⊥ BW$ , и в силу $CK ⊥ BT$ , получаем, что $L$ — точка пересечения двух высот в треугольнике $BCT.$ Значит, $TL$ — третья высота, то есть $TL ⊥ BC.$

Ошибка.
Попробуйте повторить позже

Задача 4#85482

В остроугольном треугольнике $ABC$ высоты $AH ,BH A B$ и $CH C$ пересекаются в точке $H$ . Через точки, в которых окружность радиуса $HHA$ с центром $H$ пересекает отрезки $BH$ и $CH$ , проведена прямая $ℓA$ . Аналогично проведены прямые $ℓB$ и $ℓC$ . Докажите, что точка пересечения высот треугольника, образованного прямыми $ℓA,ℓB,ℓC$ , совпадает с центром окружности, вписанной в треугольник $ABC$ .

Источники: ММО - 2024, второй день, 11.4 (см. mmo.mccme.ru)

Показать доказательство

Покажем, что биссектрисы треугольника $ABC$ содержат высоты треугольника, образованного прямыми $ℓ ,ℓ ,ℓ A B C$ . Для этого докажем, что точка пересечения прямых $ℓB,ℓC$ лежит на биссектрисе угла $∠BAC$ , а прямая $ℓA$ перпендикулярна этой биссектрисе.

_________________________________________________________________________________________________________________________________________________________________________________

Докажем, что прямая $ℓA$ перпендикулярна биссектрисе угла $∠BAC$ .

Пусть $R$ и $S$ - это точки пересечения окружности с центром в $H$ радиуса $HHA$ с отрезками $BH$ и $CH$ соответственно. Тогда треугольник $RHS$ - равнобедренный с основанием $RS$ , поэтому прямая $RS$ (она же $ℓA$ ) перпендикулярна прямой $pA$ , содержащей биссектрису угла $∠BHC$ . Поэтому достаточно доказать, что прямая $pA$ параллельна биссектрисе угла $∠BAC$ .

$PIC$

Пусть $MA$ и $NA$ — середины дуг $HCHHB$ и $⌣ HBAHC$ окружности $ωA$ , построенной на $AH$ как на диаметре. Из свойств вписанных углов следует, что $AMA$ — биссектриса $∠BAC,HNA$ — биссектриса $∠HCHHB$ . Заметим также, что $MANA$ - диаметр окружности $ωA$ . Значит, отрезки $MANA$ и $AH$ пересекаются в центре окружности $ωA$ как её диаметры и делятся точкой пересечения пополам. То есть четырёхугольник $AMAHNA −$ параллелограмм (и даже прямоугольник, поскольку его углы - вписанные, опирающиеся на диаметры окружности $ωA$ , то есть прямые). В частности, $AMA ∥HNA$ , что и требовалось.

_________________________________________________________________________________________________________________________________________________________________________________

Докажем, что прямые $ℓ B$ и $ℓ C$ пересекаются на биссектрисе угла $∠BAC$ .

Пусть прямые $ℓ B$ и $ℓ C$ пересекают отрезки $BH, CH$ в точках $P$ и $Q$ соответственно, а точку пересечения $ℓ B$ и $ℓ C$ обозначим через $X$ . Также обозначим углы $∠A,∠B$ и $∠C$ треугольника $ABC$ через $2α,2β$ и $2γ$ соответственно.

$PIC$

Поскольку $HP = HHC$ и $HQ = HHB$ , то треугольники $HHCP$ и $HHBQ$ - равнобедренные с углами, равными $∠HCHB = ∠BAC = 2α$ , напротив оснований. Поэтому $∠HP HC = ∠HQHB =90∘− α= β+ γ$ . Пусть прямые $ℓB$ и $ℓC$ пересекают отрезок $AH$ в точках $U$ и $V$ соответственно. Тогда треугольник $PUH$ - равнобедренный с основанием $PU$ , значит $∠XP H = ∠UPH = 180∘−∠2BHA-= γ$ . Рассуждая аналогично для треугольника $QV H$ , получаем, что $∠XQH = β$ . Тогда получаем

∠XP HC =∠HP HC − ∠HP X = β+ γ− γ = β =∠XQHC,

откуда следует, что $X$ лежит на окружности, описанной около треугольника $HCP Q$ . Аналогично точка $X$ лежит на окружности, описанной около треугольника $HBP Q$ . Таким образом, пять точек $X,HB$ , $P,Q,HC$ лежат на одной окружности.

Тогда по свойству вписанных углов $∠XHBHC = ∠XQHC =β$ . Четырёхугольник $BHCHBC −$ вписанный, поскольку $∠BHCC = ∠BHBC = 90∘$ . Значит, $∠HCHBC = 180∘− ∠ABC =180∘− 2β$ , то есть $∠AHBHC = 2β$ . Отсюда следует, что $HBX$ - биссектриса угла $∠AHBHC$ . Аналогично $HCX −$ биссектриса угла $∠AHCHB$ . Значит, точка $X$ является центром окружности, вписанной в треугольник $AHBHC$ , в частности, лежит на биссектрисе угла $∠BAC$ .

_________________________________________________________________________________________________________________________________________________________________________________

Повторяя рассуждения для двух других биссектрис треугольника $ABC$ , получаем, что точка пересечения биссектрис треугольника $ABC$ совпадает с точкой пересечения высот треугольника, образованного прямыми $ℓ ,ℓ ,ℓ . A B C$

Ошибка.
Попробуйте повторить позже

Задача 5#85494

В остроугольном треугольнике $ABC$ проведена высота $AH$ . Точки $M$ и $N$ - середины отрезков $BH$ и $CH$ . Докажите, что точка пересечения перпендикуляров, опущенных из точек $M$ и $N$ на прямые $AB$ и $AC$ соответственно, равноудалена от точек $B$ и $C$ .

Источники: ММО - 2024, первый день, 11.2 (см. mmo.mccme.ru)

Подсказки к задаче

Подсказка 1

Пусть перпендикуляры через M и N пересекаются в точке P. Тогда над каким дополнительным построением можно подумать, чтобы сделать MP и NP чем-то хорошим? Не забудьте, что M и N являются серединами отрезков.

Подсказка 2

Да, давайте попробуем опустить перпендикуляры X и Y из точки H на стороны треугольника. В таком случае MP и NP являются средними линиями, так как они параллельны основаниям и делят одну из сторон пополам. Но как тогда можно переформулировать вопрос задачи удобным образом для нас?

Подсказка 3

Верно, это значит, что четырёхугольник CXYB должен быть вписанным, так как в таком случае P центр описанной окружности и равноудален от B и C. Теперь только осталось посчитать уголочки, используя вписанный четырёхугольник и равные углы в прямоугольном треугольнике с проведённой высотой. Победа!

Показать доказательство

Первое решение.

Обозначим точку пересечения перпендикуляров, опущенных из точек $M$ и $N$ на прямые $AB$ и $AC$ соответственно, через $P$ , а точки, симметричные $B$ и $C$ относительно прямых $MP$ и $NP$ , через $B0$ и $C0$ . Тогда прямые $MP$ и $NP$ — cерединные перпендикуляры к отрезкам $BB0$ и $CC0$ , поэтому достаточно доказать, что четырёхугольник $BB0C0C$ — вписанный.

$PIC$

Заметим, что $MP$ и $NP$ содержат средние линии треугольников $BB0H$ и $CC0H$ , параллельные сторонам $B0H$ и $C0H$ соответственно. Значит, $HB0 ⊥ AB,HC0 ⊥ AC.$

Четырёхугольник $HB0AC0$ вписан в окружность, построенную на $AH$ как на диаметре, поэтому $∠B0C0A = ∠B0HA$ по свойству вписанных углов. При этом $∠B0HA =90∘− ∠HAB0 = ∠ABC$ . Значит, четырёхугольник $BB0C0C$ вписанный.

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение.

Обозначим точку пересечения перпендикуляров, опущенных из точек $M$ и $N$ на прямые $AB$ и $AC$ соответственно, через $P$ , а точку пересечения высот треугольника $ABC$ — через $K$ .

$PIC$

Тогда заметим, что треугольники $△BKC$ и $△NP M$ подобны по двум углам. Действительно, $∠MNP = 90∘− ∠BCA = ∠CBK$ . Аналогично, выполнено равенство $∠NMP = ∠BCK$ . Также заметим, что коэффициент подобия этих треугольников равен $2$ , поскольку $MBNC = 2$ .

Опустим из $P$ перпендикуляр $P L$ на $BC$ . Тогда из доказанного подобия следует, что $HLCM-= 2,$ т. е. $LM = NH$ . Следовательно, $BL = BM + ML = BM + NH = 12BC,$ а значит, $P$ лежит на серединном перпендикуляре к отрезку $BC$ , откуда следует требуемое.

Ошибка.
Попробуйте повторить позже

Задача 6#85508

Точки $P,Q$ лежат внутри окружности $ω$ . Серединный перпендикуляр к отрезку $PQ$ пересекает $ω$ в точках $A$ и $D$ . Окружность с центром $D$ , проходящая через $P$ и $Q$ , пересекает $ω$ в точках $B$ и $C$ . Отрезок $PQ$ лежит внутри треугольника $ABC$ . Докажите, что $∠ACP =∠BCQ$ .

Источники: Турнир городов - 2024, весенний тур, 11.2 (см. turgor.ru)

Подсказки к задаче

Подсказка 1

Про окружность ω пока толком ничего не известно, а вот окружность с центром в D даёт сразу 4 равных отрезка (равенство радиусов) на чертеже. Посмотрите, что из этого можно взять для окружности ω.

Подсказка 2

Так как BD=DC, то дуги ВD и DC в ω равны, значит, AD — биссектриса ∠BAC.

Подсказка 3

Пусть I — точка пересечения отрезка АD и дуги BPQC, тогда по теореме о трилистнике I — центр вписанной в ΔABC окружности. Что же можно взять из этого факта, если в задаче нам нужно доказать равенство углов?

Подсказка 4

Конечно! То, что CI — биссектриса ∠BСА. Для завершения доказательства не хватает равенства ∠PCI и ∠ICQ, но это совсем несложно получить, если Вы ещё не забыли, чем по условию является AD для отрезка PQ.

Показать доказательство

$PIC$

Первое решение.

Пусть $I$ — точка пересечения отрезка $AD$ и дуги $BPQC$ . Так как $DB = DC$ , то $AD$ — биссектриса угла $BAC$ и по теореме о трилистнике $I$ — центр вписанной в треугольник $ABC$ окружности. Следовательно, $CI$ — биссектриса угла $ACB$ . С другой стороны, так как $AD −$ серединный перпендикуляр к $P Q$ , то $PI = QI$ , то есть $CI$ — биссектриса угла $PCQ$ . Из этих двух утверждений следует утверждение задачи.

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение.

Обозначим $∠ACQ =α,∠QCP = β,∠PCB = γ$ . Необходимо доказать, что $γ = α$ .

Заметим, что

α+ β+ γ = ∠ACB = ∠ADB = ∠BDP +∠PDA

Далее, $∠BDP = 2∠BCP = 2γ$ , как центральный и вписанный в окружность ( $DP Q$ ), а также $∠P DA = 12∠PDQ = 12 ⋅2∠PCQ = β$ , как центральный и вписанный в окружность ( $DPQ$ ). Тогда

α+ β+ γ = ∠BDP + ∠PDA = 2γ+β

γ =α

______________________________________________________________________________________________________________________________________________________

Замечание.

В условии задачи дано, что точки $P$ и $Q$ лежат не только внутри окружности $ω$ , но и внутри вписанного в неё треугольника $ABC$ . Последнее условие на самом деле излишне. Из остальных условий задачи следует, что точки $P$ и $Q$ изогонально сопряжены относительно треугольника $ABC$ . Но если обе изогональные точки лежат внутри описанной окружности, то они лежат и внутри треугольника, поскольку при изогональном сопряжении три сегмента, ограниченные сторонами треугольника и дугами описанной окружности, переходят в три угла, вертикальных углам треугольника

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#86029

Дан треугольник $ABC, A 1$ и $B 1$ — две точки на сторонах $BC$ и $AC,$ а $P$ и $Q$ — две точки на отрезках $AA 1$ и $BB 1$ соответственно такие, что прямая $P Q$ параллельна $AB.$ На луче $P B1,$ за точку $B1$ выбрана точка $P1$ так, что $∠PP1C = ∠BAC.$ Аналогично, на луче $QA1,$ за пределами $A1,$ выбрана точка $Q1$ так, что $∠CQ1Q = ∠CBA.$ Покажите, что точки $P,Q,P1$ и $Q1$ лежат на одной окружности.

Показать доказательство

$PIC$

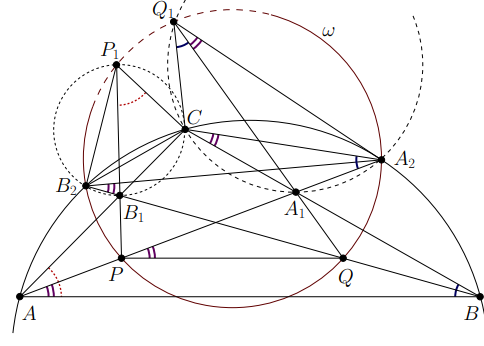
Пусть лучи $AA1$ и $BB1$ пересекают описанную окружность треугольника $ACB$ в точках $A2$ и $B2.$ Поскольку $∠QP A2 = ∠BAA2 = ∠BB2A2 =∠QB2A2,$ точки $P,Q,A2,B2$ лежат на одной окружности; обозначим эту окружность через $ω.$ Докажем, что $P1$ и $Q1$ также лежат на $ω.$

Поскольку $∠CA2A1 = ∠CA2A =∠CBA =∠CQ1Q = ∠CQ1A1,$ точки $C,Q1,A2,A1$ также лежат на одной окружности. Отсюда получаем $∠QQ1A2 =∠A1Q1A2 = ∠A1CA2 =∠BCA2 = ∠BAA2 = ∠QPA2,$ а значит $Q1$ лежит на $ω.$ Аналогично доказывается, что $P$ лежит на $ω.$

Ошибка.
Попробуйте повторить позже

Задача 8#86095

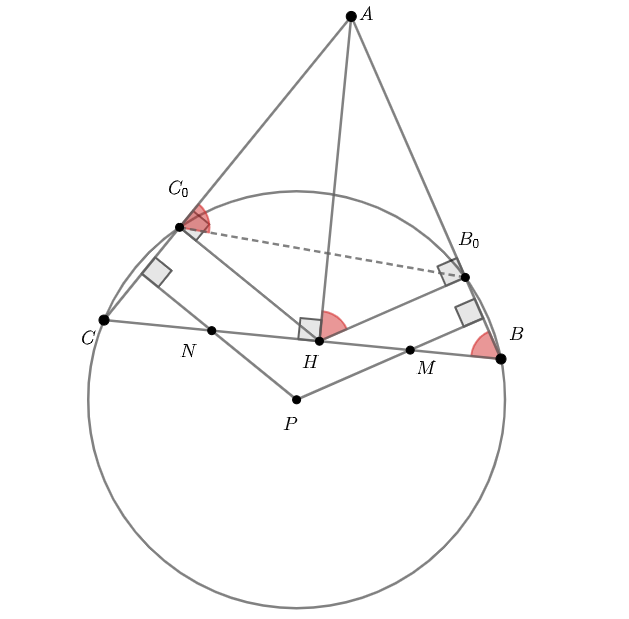
На окружности по часовой стрелке поставлены точки $A$ , $B$ , $C$ , $D$ , $E$ . Известно, что $AE =DE$ . Пересечение отрезков $AC$ и $BD$ обозначим через $P$ . На продолжении отрезка $AB$ за точку $A$ выбрали точку $Q$ так, что $AQ = DP$ . На продолжении отрезка $CD$ за точку $D$ выбрали точку $R$ так, что $AP = DR$ . Докажите, что прямые $P E$ и $QR$ перпендикулярны.

Источники: Бельчонок - 2024, 11.4 (см. dovuz.sfu-kras.ru)

Подсказки к задаче

Подсказка 1

Угол BAP равен углу BDC как вписанный, а значит углы QAP и RDP тоже равны. Треугольники QAP и RDP равны, тогда PQ=QR.

Подсказка 2

Попробуем выделить равные уголки за счет вписанных четырёхугольников ACDE и ABDE. Каким углам равны соответственно RDE и QAE?

Подсказка 3

Что можно сказать про треугольники RDE и EAP, а также EQA и EDP? Они равны по 2 сторонам и углу между ними. Следовательно QE=RE=PE, тогда что можно сказать про точку E?

Подсказка 4

Е — центр описанной окружности, а следовательно PE — часть биссектрисы в равнобедренном треугольнике, а следовательно и часть высоты

Показать доказательство

Отметим равные углы: $∠BAP = ∠BDC,$ как вписанные углы, отсюда следует, что $∠P AQ= ∠P DR.$ Рассмотрим треугольники $△P AQ$ и $△P DR.$ У них равны две стороны и угол между этими сторонами. Следовательно, эти треугольники равны, тогда $PQ = PR.$ Тогда нужно доказать , что $QE$ является частью высоты в равнобедренном треугольнике.

$PIC$

Рассмотрим вписанные четырехугольники $ACDE$ и $ABDE.$ Из вписанности получаем $∠PAE = ∠EDR$ и $∠PDE = ∠EAQ.$ Рассмотрим треугольники $△AP E$ и $△DRE.$ У них равны две стороны и угол между этими сторонами. Следовательно, эти треугольники равны, тогда $PE = ER.$ Используя аналогичные рассуждения для треугольников $△PDE$ и $△QAE,$ получаем что $P E = QE.$

В итоге получили, что точка $E$ равноудалена от вершин треугольника $△P QR,$ то есть является центром описанной окружности равнобедренного треугольника. Следовательно, $PE$ является частью высоты треугольника $△PQR,$ то есть $P E ⊥ QR.$

Ошибка.
Попробуйте повторить позже

Задача 9#87411

Дан остроугольный треугольник $ABC$ , меньший угол которого $∠ABC = 40∘$ . Внутри треугольника выбрана такая точка $D$ , что

∘ ∘ ∠BAC + ∠ADB = 180 и 2∠ACB + ∠DBA = 180.

Через точку $C$ провели прямую, параллельную прямой $AD$ , она пересекла прямую $BD$ в точке $E.$ Биссектрисы углов $∠ABD$ и $∠CAD$ пересекаются в точке $F.$ Найдите угол $∠DF E.$

Источники: СПБГУ - 2024, 11.3 (см. olympiada.spbu.ru)

Подсказки к задаче

Подсказка 1

Попробуем посчитать какие-то углы…обозначим угол DBF как х. Что интересного можно сказать о четырехугольнике AFDB?

Показать ответ и решение

Положим для краткости $∠ABF =φ$ , тогда $∠DBF = φ$ и $∠DBA =2φ$ . По условию

∘ 2∠ACB +2φ =2∠ACB + ∠DBA = 180

и, значит, $∠ACB =90∘− φ$ .

∘ ∘ ∘ ∠BAD =180 − ∠DBA − ∠ADB = 180 − 2φ− (180 − ∠BAC )=∠BAC − 2φ.

Следовательно,

∠DAF = ∠DAC-= ∠BAC--− ∠BAD = φ 2 2

и четырехугольник $AF DB$ вписанный.

Таким образом, $∠ADF = ∠ABF = φ$ , значит, треугольник $AFD$ равнобедренный и, в частности, $F A= FD$ . Поскольку $AF −$ биссектриса угла $∠CAD$ , а прямые $AD$ и $CE$ параллельны, $∠ACE =∠CAD =2φ =∠ABE$ . Следовательно, четырехугольник $AECB$ является вписанным

$PIC$

В силу вписанности

∘ ∠AF-D ∠AED =∠AEB =∠ACB =90 − φ= 2 ,

стало быть, точка $F$ является центром описанной окружности треугольника $ADE$ и, значит, $∠DF E = 2∠DAE$ . Осталось заметить, что

∠DAE =180∘− AED − ∠ADE = 180∘− ∠ACB − ∠BAC = ∠ABC = 40∘,

откуда получаем ответ $∠DF E =80∘$ .

Ответ:

$80∘$

Ошибка.
Попробуйте повторить позже

Задача 10#87882

Пусть $M$ и $N$ — середины “меньшей” и “большей” дуг $BC$ описанной окружности треугольника $ABC$ соответственно. Докажите, что

(a) $AM$ — биссектриса угла $BAC$ ;

(b) $AN$ — биссектриса внешнего угла $BAC$ .

Показать доказательство

$M$ — середина “меньшей” дуги $BC,$ то есть дуги $MB$ и $MC$ равны. Тогда будут равны и вписанные углы $∠BAM =∠MAC,$ опирающиеся на равные дуги одной окружности. Значит, $AM$ — биссектриса угла $BAC.$

$PIC$

$M$ и $N$ — диаметрально противоположные точки, так как эти точки — середины “меньшей” и “большей” дуги $BC$ соответственно. Следовательно, вписанный угол $∠NAM =90∘,$ как опирающийся на диаметр.

Тогда

∠CAN =90∘− ∠MAC =90∘− 1∠BAC = 1(180∘ − ∠BAC ) 2 2

Значит, $AN$ делит пополам внешний угол, смежный с $BAC$ , то есть является биссектрисой внешнего угла $BAC.$

Ошибка.
Попробуйте повторить позже

Задача 11#87884

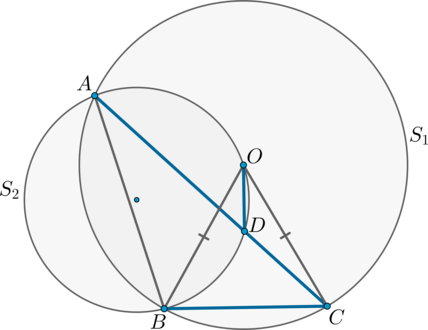
Окружности $S 1$ и $S 2$ пересекаются в точках $A$ и $B$ , центр $O$ окружности $S 1$ лежит на окружности $S 2$ . Хорда $AC$ окружности $S 1$ пересекает окружность $S2$ в точке $D$ . Оказалось, что $D$ лежит внутри треугольника $BOC$ . Докажите, что отрезки $OD$ и $BC$ перпендикулярны.

Подсказки к задаче

Подсказка 1

Проведите отрезки OB, OC и AB. Каким является треугольник BOC? Две его стороны являются чем-то хорошим в окружности...

Подсказка 2

Действительно, треугольник BOC − равнобедренный. Нужно доказать, что OD принадлежит высоте, проведенной к основанию BC. Но высота в этом треугольнике является и биссектрисой. Давайте доказывать равенство углов BOD и COD. Какому углу равен вписанный в окружности S2 угол BOD?

Подсказка 3

BOD = BAD, ведь они опираются на дугу BD. А теперь посмотрите на окружность S1 − каким является угол BAD (то же самое, что угол BAC) в этой окружности? Чему он равен?

Подсказка 4

Он равен половине градусной меры дуги BC. А каким является угол BОC в этой окружности? Чему он равен?

Подсказка 5

Он равен градусной мере дуги как центральный угол. Так получается, что угол BOC в два раза больше угла BOD. Значит, OD делит угол пополам, точка D лежит на биссектрисе, а значит, и на высоте − задача решена!

Показать доказательство

Проведем отрезки $OB, OC,AB.$ Заметим, что $△BOC$ равнобедренный, следовательно, необходимо доказать, что прямая $OD$ содержит высоту, опущенную к основанию $BC.$

Докажем, что прямая $OD$ содержит биссектрису $∠BOC,$ тогда отсюда будет следовать утверждение задачи. Таким образом, необходимо доказать, что $∠BOD = ∠COD.$

$PIC$

Заметим, что вписанные углы окружности $S2,$ опирающиеся на одну и ту же дугу $B⌣D ,$ равны:

∠BOD = ∠BAD = α

С другой стороны, $∠BAC,$ он же $∠BAD$ , — вписанный угол окружности $S1,$ опирающийся на дугу $⌣ BC ,$ следовательно,

⌣ BC= 2∠BAC = 2α

Так как $∠BOC$ — центральный угол окружности $S1,$ опирающийся на дугу $⌣ BC ,$ то

⌣ ∠BOC = BC= 2α

Отсюда имеем:

∠COD = ∠BOC − ∠BOD = 2α− α= α

Следовательно, $OD$ — часть биссектрисы равнобедренного треугольника $BOC,$ а следовательно, и часть высоты.

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#89903

В четырёхугольнике $ABCD$ внешний угол при вершине $A$ равен углу $∠BCD, AD =CD.$ Докажите, что $BD$ — биссектриса угла $ABC.$

Подсказки к задаче

Подсказка 1

Внешний угол при вершине A равен углу при вершине С. Что тогда можно сказать про сумму углов DAB и BСD? А про сам четырехугольник?

Подсказка 2

Сумма этих углов равна 180 градусов, а значит четырехугольник ABCD вписанный! Теперь воспользуемся вторым условием и вспомним, что равные хорды стягивают равные дуги, а на равные дуги описаются равные углы.

Показать доказательство

Т.к. внешний угол при вершине $A$ равен углу $∠BCD,$ то по признаку четырёхугольник $ABCD$ является вписанным.

$PIC$

Значит, раз $AD =CD,$ то $∠ABD$ и $∠DBC$ опираются на равные дуги, следовательно, $∠ABD =∠DBC,$ т.е. $BD$ — биссектриса $∠ABC.$

Ошибка.
Попробуйте повторить позже

Задача 13#89937

Докажите, что все углы, образованные сторонами и диагоналями правильного $n$ -угольника, могут быть представлены как $180∘⋅k- n$ для некоторого натурального $k$ (для разных углов это $k$ может быть разным).

Подсказки к задаче

Подсказка 1

Поскольку мы имеем дело с правильным n-угольником, полезной идеей может быть рассмотреть описанную около него окружность.

Подсказка 2

Давайте поймём, откуда у нас могут появиться углы вида 180k/n и почему все рассматриваемые углы выражаются ровно так.

Подсказка 3

Итак, рассматриваемые нами углы - углы между прямыми, содержащими хорды окружности, описанной около многоугольника. Для них есть формулы, выражающие их через дуги, на которые опираются хорды. Осталось понять, чему могут быть равны величины дуг, на которые опираются хорды.

Показать доказательство

Углы, образованные сторонами и диагоналями правильного $n−$ угольника — это углы между прямыми, содержащими хорды, а значит равны полусумме либо полуразности дуг. Угловые меры дуг в правильном $n−$ угольнике вида $360∘⋅k- n$ для какого-то натурального $k.$ Ясно, что полусумма и полуразность углов такого вида будет иметь вид $180∘⋅k n$ для какого-то целого $k,$ и поскольку углы имеют какую-то величину, $k$ является положительным, а значит, натуральным.

Ошибка.
Попробуйте повторить позже

Задача 14#89939

Дан равнобедренный треугольник $ABC$ $(AB = BC).$ На меньшей дуге $AB$ описанной около него окружности взята точка $D.$ На продолжении отрезка $BD$ за точку $D$ выбрана точка $E.$ Описанная окружность треугольника $AED$ пересекает сторону $AB$ в точке $F.$ Докажите, что прямые $EF$ и $AC$ параллельны.

Подсказки к задаче

Подсказка 1

Раз уж речь про равнобедренный треугольник, пару вписанных четырёхугольников, и доказать требуют параллельность, логично заняться переписыванием равных уголочков.

Подсказка 2

Для этих целей идеально подойдёт уголок CAB, сразу видно равный ему уголок, также ясно, что доказывать стоит его равенство с EFA.

Подсказка 3

Итак, из равнобедренности ABC CAB=CBA. Теперь с помощью вписанностей нужно найти равный им уголок поближе к прямой EF.

Показать доказательство

Поскольку $AB =BC,$ углы $∠CAB = ∠BAC.$ Из вписанности $ACBD$ следует $∠ABC + ∠ADC = 180∘.$ Тогда угол, смежный $∠ADC,$ то есть угол $∠EDA,$ равен $∠ABC.$ В свою очередь из вписанности $AEDF$ получаем $∠EDA = ∠EFA.$ Итак, мы доказали, что $∠CAB =∠EF A.$ А из равенства таких уголочков следует $AC||EF.$

$PIC$

Ошибка.
Попробуйте повторить позже

Задача 15#89940

В остроугольном треугольнике $ABC$ через центр $O$ описанной окружности и вершины $B$ и $C$ проведена окружность $S.$ Пусть $OK$ — диаметр окружности $S,D$ и $E$ соответственно точки ее пересечения с прямыми $AB$ и $AC.$ Докажите, что $ADKE$ — параллелограмм.

Подсказки к задаче

Подсказка 1

Нам даны окружности, доказать требуется параллельность. Логично тогда посчитать какие-нибудь уголочки. Докажем равенство углов ∠BAC=∠BDK.

Подсказка 2

Заметим, что точка K лежит на серединном перпендикуляре к BC. Какие выводы из этого можно сделать?

Подсказка 3

Верно, ∠BOK=∠COK. Самое время воспользоваться вписанностью BDOK и завершить доказательство параллельности AC и DK. Аналогично докажем параллельность другой пары сторон параллелограмма.

Показать доказательство

Поскольку $O$ — центр описанной окружности $ABC$ получаем $∠BCO =2⋅∠BAC.$ Центр описанной около $OBC$ окружности лежит на серединном перпендикуляре к $BC,$ как и точка $O,$ тогда точка $K$ лежит на нём же. Тогда $∠BOK = ∠COK,$ значит, $∠BOK = ∠BAC.$ Из вписанности $BDOK$ знаем, что $∘ ∠BOK = 180 − ∠BDK.$ Итак, $∘ ∠BAC =180 − ∠BDK,$ а значит, $AC ||DK,$ по аналогии доказывается, что $AB ||EK.$ Таким образом, в четырёхугольнике $ADKE$ пары противоположных сторон параллельны, а значит он является параллелограммом.

$PIC$

Ошибка.
Попробуйте повторить позже

Задача 16#90904

Окружность, вписанная в угол с вершиной $O,$ касается его сторон в точках $A$ и $B,K$ — произвольная точка на меньшей из двух дуг $AB$ этой окружности. На прямой $OB$ взята точка $L$ такая, что прямые $OA$ и $KL$ параллельны. Пусть $M$ — точка пересечения окружности $ω,$ описанной около треугольника $KLB,$ с прямой $AK,$ отличная от $K.$ Докажите, что прямая $OM$ касается окружности $ω.$

Подсказки к задаче

Подсказка 1

В задаче есть какие-то углы. Никогда не бывает лишним поотмечать уголочки. Можно заметить вписанность, коллинеарность, подобие. Найдите что-нибудь из этого в этой задаче.

Подсказка 2

Оказывается, что можно понять многое счетом углов. Докажите, что ABMO - вписанный, BKM - равнобедренный. Поймите, как перейти от равнобедренности к касанию.

Подсказка 3

Касательная в вершине равнобедренного треугольника имеет понятное направление. Тогда нужно доказывать, что OM || BK. Поймите это, посчитав углы.

Показать доказательство

Покажем, что $M$ лежит на окружности $(OAB ).$ Действительно, $∠AOB = ∠KLB = ∠KMB,$ откуда имеем требуемое.

$PIC$

Докажем, что $KM = MB.$ Пусть $D$ — точка, диаметрально противоположная точке $O$ в окружности $(AOB ).$ Тогда $∠BDA =180∘− ∠AOB.$ Тогда, поскольку D — центр описанной окружности $(KLB )$

∠AKB =180∘− ∠BDA-= 90+ ∠AOB- 2 2

следовательно, $∠MKB = 90− ∠AOB-=∠OAB. 2$ Кроме этого, $∠AOB =∠AMB$ в силу вписанности четырехугольника $AOMB.$ Таким образом, треугольник $KMB$ подобен треугольнику $AOB,$ следовательно, является равнобедренным.

Наконец, $MO$ — биссектриса внешнего угла $AMB,$ поскольку $O$ — центр дуги $AB$ окружности $AMB,$ следовательно, $KB || OM,$ то есть, поскольку $M$ — середина дуги $KB$ окружности $ω,$ прямая $OM$ касается $ω.$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#91436

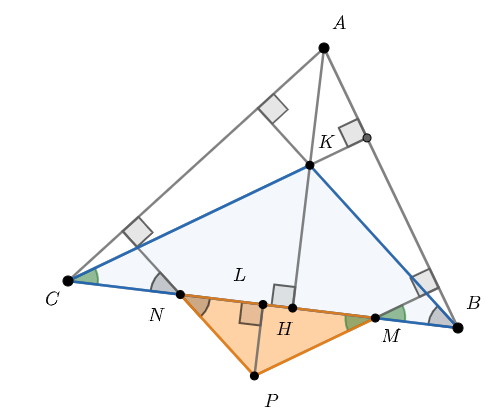
В остроугольном треугольнике $ABC$ проведены высоты $AA 1$ и $CC . 1$ Из точек $A 1$ и $C 1$ опустили перпендикуляры на прямые $AB$ и $BC.$ Докажите, что прямая, проходящая через основания этих перпендикуляров, параллельна $AC.$

Подсказки к задаче

Подсказка 1

Как правило, параллельность доказывается через равенство каких-нибудь углов, например, соответственных. Попробуйте посчитать углы.

Подсказка 2

Для этого поищите вписанные четырёхугольники. Найдите равные углы, стягивающие один и тот же отрезок.

Показать доказательство

Обозначим основания перпендикуляров через $X$ и $Y.$

$PIC$

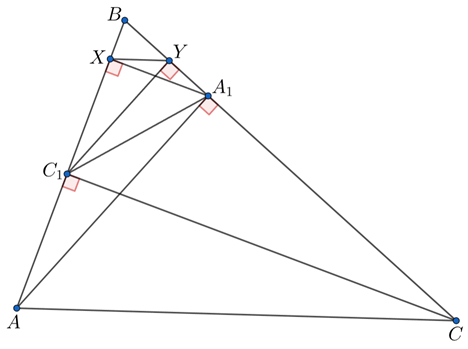
Заметим, что четырёхугольники $AC1A1C$ и $C1XY A1$ вписанные. Значит, $∠C1AC = ∠YA1C1 = ∠BXY.$ Это и даёт параллельность.

Ошибка.
Попробуйте повторить позже

Задача 18#91437

В равнобедренном треугольнике $ABC (AC =BC )$ точка $O$ — центр описанной окружности, точка $I$ — центр вписанной окружности, а точка $D$ на стороне $BC$ такова, что прямые $OD$ и $BI$ перпендикулярны. Докажите, что прямые $ID ∥AC.$

Подсказки к задаче

Подсказка 1

Для начала подумайте над взаимным расположением точек I и O. Стоит ли рассмотреть несколько случаев?

Подсказка 2

Поищите на рисунке вписанные четырёхугольники. Впрочем, на рисунке четырëхугольников не слишком много.

Подсказка 3

Проведите высоту CE, проходящую через O и I. Подумайте, как еë наличие может помочь в реализации предыдущей подсказки.

Показать доказательство

Если данный треугольник равносторонний (точки $O$ и $I$ совпадают), то утверждение очевидно.

Проведём высоту $CE.$ Пусть точка $O$ лежит между точками $I$ и $∘ C (∠B > 60),$ а прямые $OD$ и $BI$ пересекаются в точке $K.$ Положим $∠B =∠A = 2α.$ Тогда

∘ ∘ ∘ ∠EBI =∠DBI =α,∠BIE = 90 − α =∠BDK, ∠BIO = 180 − ∠BIE = 90 + α

$PIC$

Сумма противоположных углов $BIO$ и $BDO$ четырёхугольника $BIOD$ равна $180∘,$ то есть он — вписанный. Вписанные углы $BDI$ и $BOI$ его описанной окружности равны. Кроме того, $BOI$ — внешний угол равнобедренного треугольника $BOC.$ Значит,

∠BDI =∠BOI = 2∠BCE = 180∘ − 4α =∠DCA

Следовательно, $DI ∥AC.$

Случай, когда точка $I$ лежит между точками $O$ и $∘ C(∠B < 60 ),$ разбирается аналогично.

Ошибка.
Попробуйте повторить позже

Задача 19#91979

Вокруг остроугольного треугольника $ABC$ описана окружность. На дуге $CA$ (не содержащей точку $B$ ) этой окружности отмечена некоторая точка $P$ . Прямая, проходящая через точки $B$ и $H$ , где $H$ — точка пересечения высот треугольника $ABC$ , пересекает отрезок $AP$ в точке $Q$ . Найдите отношение $AC$ к $BC$ , если известно, что точки $C,P,Q,H$ лежат на одной окружности.

Источники: ДВИ - 2024, вариант 242, задача 5 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Вспомните свойства вписанных четырёхугольников, что мы можем сказать об их противоположных углах? Итак, ∠CHQ + ∠CPQ = 180°, попробуем связать каждый из этих углов с углами △АВС.

Подсказка 2

Свойства вписанных четырёхугольников помогут нам с ∠CPQ, а работа с прямоугольными треугольниками поможет с ∠CHQ. Сделайте вывод!

Показать ответ и решение

$PIC$

Заметим, что

∠AHcH + ∠AHbH = 90∘+90∘ = 180∘,

поэтому четырёхугольник $AHbHHc$ вписанный, а значит, $∠A = ∠CHQ.$

Точки $A,B,C,P$ лежат на одной окружности по условию, поэтому

∠AP C = 180∘ − ∠B.

Вспоминая то, что по условию ещё и точки $C,P,Q,H$ лежат на одной окружности, получим:

∘ ∠CHQ = 180 − ∠AP C = ∠B

Значит, $∠A= ∠B =⇒ AC = BC.$

Ответ: 1 : 1

Ошибка.
Попробуйте повторить позже

Задача 20#92116

На стороне $BC$ остроугольного треугольника $ABC$ отмечена точка $D$ , отличная от $B$ и C. Пусть $E$ — точка пересечения отрезка $AC$ с окружностью, описанной около треугольника $ABD$ , отличная от $A$ . Пусть $F$ — точка пересечения отрезка $AB$ с окружностью, описанной около треугольника $ACD$ , отличная от $A$ . Пусть $′ ′ ′ D ,E ,F$ — точки пересечения окружности, описанной около треугольника $ABC$ , с прямыми $AD,BE,CF$ соответственно, отличные от точек $A,B,C$ . Найдите угол $′ ′′ ∠E D F$ , если известно, что $∘ ∠EDF =30 .$

Источники: ДВИ - 2024, вариант 243, задача 5 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Из условия понятно, что, так как многие точки были построены как пересечение окружностей с прямыми, на картинке есть вписанные четырехугольники (и, следовательно, углы). Быть может, тогда рассмотрим, чему равны части нужного нам угла?

Подсказка 2

Нужный нам угол состоит из двух частей, обе из которых вписаны в окружность (ABC). Какие углы, вписанные в эту же окружность, им равны?

Подсказка 3

Углы ∠AD’E´и ∠ABE’ равны, аналогично и ∠AD’F’ с ∠ACF’. То есть вместо одного угла нам нужно посчитать сумму углов ∠ABE’ и ∠ACF’. А в каких вписанных четырехугольниках они присутствуют?

Подсказка 4

∠ABE’ расположен во вписанном четырехугольнике ABDE, а ∠ACF’ — в ACDF!

Показать ответ и решение

Докажем, что $∠E ′D′F′ = ∠EDF.$ Для этого покажем, что они состоят из одинаковых углов.

$PIC$

$∠AD′F′ = ∠ACF′,$ так как они опираются на одну дугу окружности, описанной около треугольника $ABC.$ А также из того, что $AF DC$ вписанный следует, что $∠ACF ′ = ∠ADF.$

Таким образом, показано, что $∠AD′F′ = ∠ADF.$ Совершенно аналогично доказывается, что $∠AD ′E ′ =∠ADE.$

В итоге $∠E′D′F ′ =∠EDF = 30∘.$

Ответ:

$30∘$

Предыдущий раздел

Следующий раздел