Тема Окружности

Касание с окружностью и касание окружностей

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела окружности

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#64954

В неравнобедренном треугольнике $ABC$ серединные перпендикуляры к сторонам $AB$ и $AC$ пересекают высоту из вершины $A$ в точках $P$ и $Q$ соответственно. Найдите радиус описанной около этого треугольника окружности, если $AP =a,AQ = b.$

Источники: Муницип - 2024, 9 класс

Показать ответ и решение

Пусть для определенности углы $B,C$ — острые, обозначим $∠B = β,∠C = γ$ . Так как $AP$ — высота, то $∠BAP = π− β,∠CAP = π− γ. 2 2$ Пусть $E,K$ — середины $AB,AC$ соответственно.

Первое решение.

$PIC$

Отметим точку $O$ пересечения серединных перпендикуляров $EP$ и $KQ$ к сторонам треугольника $ABC$ . Эта точка является центром описанной около треугольника окружности. Заметим, что угол $AOK$ вдвое меньше центрального угла $AOC,$ поэтому равен вписанному углу $ABC,$ то есть $β.$ При этом $∠APE = ∠B = β$ из вписанности четырёхугольника $BEP H$ (два прямых угла дают вписанность). Тогда обратим внимание, что $AO$ касается описанной окружности треугольника $OQP$ , так как угол между ней и хордой $OQ$ равен углу $OPQ,$ опирающемуся на эту хорду. По теореме о касательной и секущей получаем $AO2 = AQ ⋅AP = a⋅b.$

Второе решение.

$PIC$

Не будем думать и посчитаем в синусах: из прямоугольных треугольников

AE =asinβ,AK =bsinγ =⇒ AB = 2asinβ,AC =2bsinγ

Тогда получается

AB AC sinβ √b sin-γ = sinβ =⇒ sinγ = √a

Наконец, по теореме синусов радиус описанной окружности равен

-AB-- √ -- 2sinγ = ab

Ответ:

$√ab$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#76189

Дед Мороз нарисовал на снегу две окружности с радиусами $2023$ и $r> 2023$ , которые касаются друг друга и ветвей параболы $y = x2$ . Найдите $r.$

Показать ответ и решение

Первое решение.

Посмотрим при каких условиях окружность касается параболы. Пусть есть окружность радиуса $R1$ с центром в точке $A$ , $B$ — точка касания окружности и параболы. Проведем касательную $BE$ . Тогда $∘ ∠ABE = 90$ .

$PIC$

Проведем через точку $B$ прямую, параллельную оси $Ox$ ( $C$ — точка пересечения прямой и оси $Oy$ ). Тогда $∠CBA +∠EBC1 = 90∘$ . Значит, $tg∠EBC1 = ctg∠ABC$ , но $tg∠EBC1 = 2x1$ , так как $EB$ — касательная $y = x2$ в точке $x1$ .

Значит, $CB 1 AC-= 2x1 ⇒ AC = 2$ . Тогда по теореме Пифагора получаем, что $1 R21 = x21 +4$ .

Теперь рассмотрим случай с двумя окружностями

$PIC$

Пусть $CB =x1$ и $C1B1 = x2$ . Тогда

R2= x2+ 1 1 1 4

2 2 1 R2 = x2+ 4

R22− R21 = x22− x21 (1)

Также знаем, что

2 2 R2 +R1 =CC1 = x2− x1 (2)

Из (1) и (2) получаем

R2 − R1 = 1⇒ R2 = R1+ 1= 2023+1 =2024

Второе решение.

Пусть $(0,Y)$ — координаты центра первой окружности. Тогда $(0,Y + 2023+ r)$ — координаты центра второй окружности, где $r$ — искомый радиус.

$PIC$

Запишем систему уравнений для первой (1) и второй (2) окружности. Первое уравнение – пересечение окружности и параболы. Второе – условие касания

( |{ x2+ (x2− Y)2 = 20232 |( −-21-- = 2 x − Y

(|{ 2 1 Y =20231+ 4 |( x2 = Y − 2

( ||{ x2+ (x2− (Y + 2023+ r))2 = r2 | −----------1----------= 2 |( x2− (20232+ 1+ 2023+ r) 4

({x2+ (x2− (Y +2023+ r))2 = r2 ( 2 1 x =− 2 + (Y + 2023+ r)

Получаем, что $2 2 2023 + 2023 +r= r ⇒ r1 = −2023$ и $r2 = 2024$ . Так как $r≥ 0$ , то нам подходит только $r2 = 2024.$

Ответ: 2024

Ошибка.
Попробуйте повторить позже

Задача 3#76652

Окружности $ω 1$ и $ω 2$ пересекаются в точках $A$ и $B$ . Прямая $l 1$ , проходящая через точку $A$ , второй раз пересекла окружность $ω 1$ в точке $C$ , а $ω2$ — в точке $D$ . Прямая $l2$ , проходящая через точку $B$ , второй раз пересекла окружность $ω1$ в точке $E$ , а $ω2$ — в точке $F.$ Оказалось, что прямая $CE$ касается $ω2$ в точке $G$ (точка $E$ лежит на отрезке $CG$ ). Докажите, что $BG$ — биссектриса $∠DBE$ .

Источники: по мотивам отборочного тура ЮМШ 23/24

Подсказки к задаче

Подсказка 1

Посчитаем уголочки! Как использовать вписанность? Выразим угол FBE и подумаем, как считать углы дальше.

Подсказка 2

Угол между касательной равен вписанному углу, опирающему на хорду. Найдите угол DFC и свяжите его с DAF :) Чему равен угол FBE?

Показать доказательство

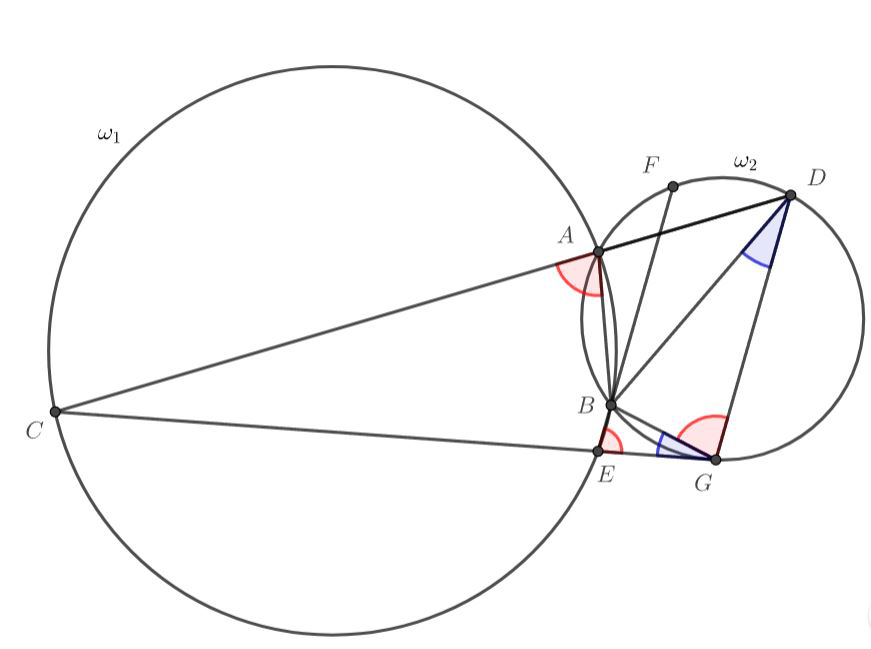
Поскольку четырехугольники $ABEC$ и $ADGB$ вписанные, то

∠BEG = ∠CAB = ∠BGD

Также, поскольку прямая $CE$ касется окружности $ω2$ , по теореме об угле между касательной и хордой

∠BDG = ∠BGE

Теперь рассмотрим треуугольники $△BEG$ и $△BGD.$ В них имеются две пары равных углов $(∠BEG = ∠BGD, ∠BGE = ∠BDG ),$ значит, третьи углы у них тоже равны, т.е.

∠DBG = ∠GBE

Получаем, что $BG$ — биссектриса угла $∠DBE.$

$PIC$

Замечание. Если точка $G$ лежит внутри отрезка $CE,$ то чертёж меняется, но решение остаётся аналогичным. Попробуйте решить задачу и для этого расположения точек.

Ошибка.
Попробуйте повторить позже

Задача 4#76754

Три окружности с центрами в точках $A,B,C$ и радиусами $a= 1,b= 2,c=3$ соответственно попарно касаются друг друга внешним образом в точках $X,Y,Z.$ Найдите радиус описанной окружности треугольника $XY Z.$

Показать ответ и решение

Заметим, что точки $X, Y, Z$ лежат на сторонах $AB, BC, AC$ соответственно, так как радиусы в точку касания перпендикулярны общей касательной в этой точке.

Докажем, что линии центров $AB, BC, AC$ являются касательными к окружности, описанной около треугольника $XY Z.$

$PIC$

$AX =AZ, BY =BY, CZ = CY$ как отрезки касательных.

Обозначим $∠BAC =α, ∠ABC =90∘− α$ . Считая углы, получаем, что $∠AXZ = ∠XYZ$ , а значит, по критерию касательной $XA$ касается окружности, описанной около $XY Z$ . Аналогично для остальных отрезков. Итого получаем, что окружность, вписанная в $ABC$ , совпадает с окружностью, описанной около $XY Z.$

Треугольник $ABC$ со сторонами $3, 4, 5$ — прямоугольный. Радиус вписанной в него окружности равен

S- --42⋅3- p = 3+52+4-= 1

Ответ: 1

Ошибка.
Попробуйте повторить позже

Задача 5#79332

Высоты $AA ,BB ,CC 1 1 1$ остроугольного треугольника $ABC$ пересекаются в точке $H.$ Пусть $M$ — середина стороны $BC,K$ — середина $B1C1.$ Докажите, что окружность, проходящая через $K,H$ и $M,$ касается $AA1.$

Показать доказательство

$PIC$

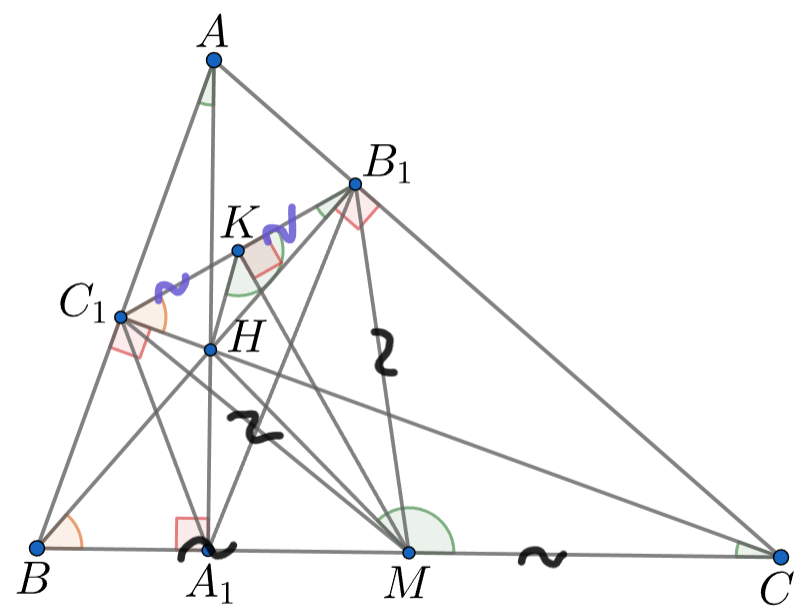
Заметим, что отрезок $BC$ виден под прямым углом из точек $B1$ и $C1.$ Значит, точки $B,C,B1,C1$ лежат на одной окружности с центром в точке $M.$ Поскольку $MK$ является медианой, направленной к основанию равнобедренного треугольника $B1C1M$ , она же является высотой. Заметим, что $∠BCC1 = 90∘− ∠B = ∠BAH = ∠C1B1B,$ так как четырёхугольник $AB1HC1$ вписанный $(∠AC1H = ∠AB1H = 90∘).$ Аналогично $∠B1C1C = ∠B1BC.$ Значит, треугольники $BCH$ и $C1B1H$ подобны. Точки $K$ и $M$ являются серединами соответствующих сторон, так что подобны также $B1HK$ и $CHM.$ Отсюда $∠B1KH =∠CMH.$ Тогда $∠MKH = ∠HKB1 − 90∘ = 90∘ − ∠A1MH = ∠MHA1.$ Значит, по свойству касательной прямая $AA1$ касается окружности, описанной около $MHK.$

Ошибка.
Попробуйте повторить позже

Задача 6#80767

Две окружности $ω 1$ и $ω 2$ пересекаются в точках $A$ и $B$ , общая касательная касается окружностей $ω 1$ и $ω 2$ в точках $C$ и $D$ соответственно (точка $B$ лежит ближе к $CD$ , чем точка $A$ ). Луч $CB$ пересекает окружность $ω2$ в точках $B$ и $E$ . Найдите $ED :CD$ , если диагональ $AD$ четырехугольника $ACDE$ делит прямую $CE$ в отношении $3:10,$ считая от вершины $C$ .

Источники: Физтех - 2024, 11.4 (см. olymp-online.mipt.ru)

Подсказки к задаче

Подсказка 1

Сразу попробуем воспользоваться условием и отметим равные углы. А чему равен угол ACD? Как воспользоваться тем, что CD - касательная?

Подсказка 2

Угол ADC равен AED, а угол ACD равен 180 - ABC. Что полезного можно вывести из этого? Как поближе подобраться к углам треугольника AED?

Подсказка 3

Угол ABE равен углу ACD (почему?). Как воспользоваться вписанностью? Нам было бы очень хорошо, если бы мы понимали, как воспользоваться тем, на какие отрезки AM делит AM...

Подсказка 4

Оказывается, треугольники AED и ADC подобны! Тогда что можно сказать интересного о прямой AM?

Подсказка 5

Это биссектриса угла AEC! Как воспользоваться найденным подобием? Вспоминаем свойство биссектрисы и находим требуемую дробь!

Показать ответ и решение

$PIC$

Отметим равные углы. $∠ADC = ∠AED,$ по свойству угла между касательной и хордой. Градусная мера угла $∠ACD$ вдвое меньше дуги $AC,$ содержащую $B,$ окружности $ω1,$ по свойству угла между касательной и хордой. Тогда $∠ABC = 180∘− ∠ACD,$ так как градусная мера дуги $AC,$ не содержащую $B$ равняется $360∘− 2∠ACD.$ Следовательно, $∠ABE = ∠ACD.$ Также $∠ACD =∠ADE,$ как вписанные. Из этого следует, что треугольники $△AED$ и $△ADC$ подобны. Это значит, что $∠EAD = ∠DAC,$ то есть $AM$ — биссектриса угла $∠EAC.$ Запишем соотношения из подобия $△AED$ и $△ADC$

( ) ED-= EA-= AD- =⇒ ED- 2 = EA- CD AD AC CD AC

По теореме о биссектрисе $AM$ получаем

EA EM 10 AC-= MC- = 3-

Тогда получаем, что

( )2 √-- ED- = EA-= EM- = 10- =⇒ ED- = √10 CD AC MC 3 CD 3

Ответ:

$√10-:√3$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#82291

Окружности $S 1$ и $S 2$ находятся внутри трапеции $ABCD$ , касаясь друг друга, оснований трапеции, и каждая — своей боковой стороны. Лучи $AB$ и $DC$ пересекаются в точке $K$ . Оказалось, что радиус вписанной окружности треугольника $BCK$ равен радиусу окружности $S1$ и равен $r.$ Также известно, что $BC = x$ . Найдите площадь треугольника $ADK.$

Источники: ИТМО-2024, 11.6 (см. olymp.itmo.ru)

Подсказки к задаче

Подсказка 1

Для начала нужно заметить, что радиусы двух окружностей S1 и S2 равны (доказать этот факт не составит труда). После этого надо вписать окружность, которая является вписанной для BCK, в трапецию. Далее можно отметить все точки касания, равные углы и, может быть, заметить какие-то равенства.

Подсказка 2

После того, как мы отметили все равные отрезки, останется выразить высоту треугольника АDK через известные нам величины и найти площадь.

Показать ответ и решение

Радиусы $S 1$ и $S 2$ равны друг другу и высоте трапеции. Из условия про пересечение лучей следует, что $BC$ — меньшее основание.

Проведём вторую касательную к вписанной окружности треугольника $BCK$ параллельную основаниям трапеции. Обозначим за $X$ и $Y$ точки пересечения этой касательной с отрезками $BK$ и $CK.BXY C$ — трапеция.

Точки касания окружностей и оснований трапеции образуют квадрат со стороной $2r$ . Если вырезать этот квадрат из трапеции и склеить оставшиеся части между собой, получится трапеция, равная $BXY C$ .

Более точно, обозначим точки касания окружностей $S1$ и $S2$ с основаниями трапеции $ABCD$ : пусть $M$ и $N$ лежат на $BC$ ( $M$ ближе к $B$ ), $P$ и $Q$ лежат на $AD$ ( $P$ ближе к $A$ ). Кроме того, пусть $U,V,W,Z$ - точки касания вписанной окружности $BCK$ с $XY,BC,BK, CK$ соответственно. Кроме того, пусть $R$ и $T$ - точки касания окружностей $S1$ и $S2$ с боковыми сторонами трапеции, $O1,O2$ и $O$ - центры окружностей $S1,S2$ и вписанной окружности треугольника $BCK$ .

$PIC$

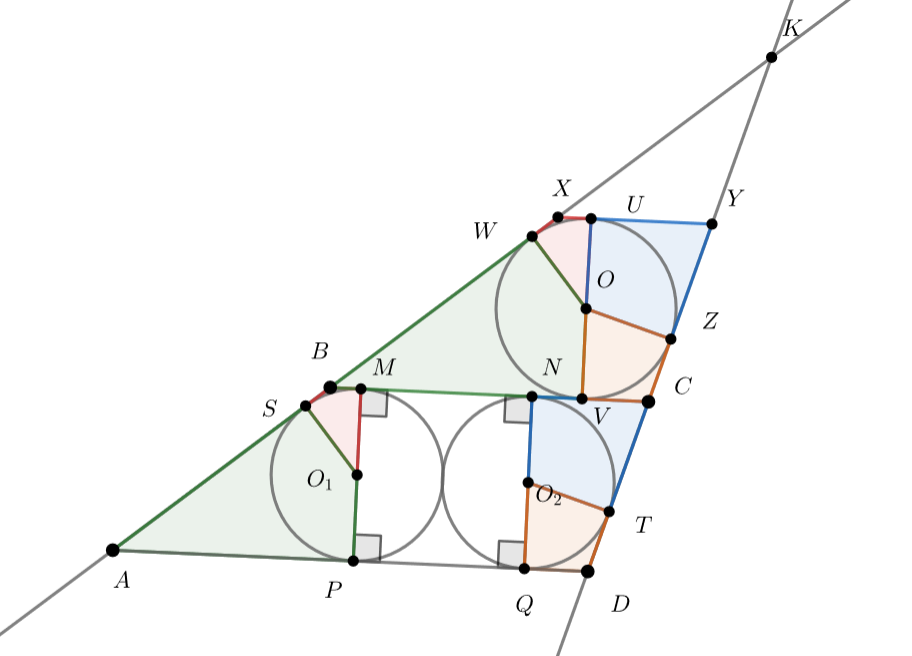
Рассмотрим четырёхугольники $SBMO1$ и $W XUO :$

$∠SBM = ∠W XU,$ как соответственные. $∠O1SB,∠BMO1, ∠OW X$ , $∠XUO$ прямые.

Значит оставшиеся углы, $∠MO1S$ и $∠UOW$ также равны. Значит, треугольники $MO1S$ и $UOW$ равны. Следовательно, треугольники $SBM$ и $W XU$ также равны, а значит четырёхугольники $SBMO1$ и $W XUO$ равны. Аналогично

SAP O1 = WBV O,TDQO2 = ZCV O,TCNO2 = ZYUO

Значит,

BC = BV +CV = AP + QD =AD − PQ = AD − 2r

AD =BC + 2r= x+ 2r

Пусть $h$ - длина высоты треугольника $BCK$ , проведённой из точки $K$ . Тогда длина высоты треугольника $ADK$ , проведённой из точки $K$ равна $h+ 2r$ . Значит, коэффициент подобия треугольников $ADK$ и $BCK$ с одной стороны равен $h+2r- h$ , а с другой $AD- x+2r BC = x$ , откуда $h= x$ . Значит, площадь треугольника $ADK$ равна

AD ⋅(h+2r) (x+ 2r)2 ----2-----= ---2---

Ответ:

$(x+-2r)2 2$

Ошибка.
Попробуйте повторить позже

Задача 8#85176

Окружности радиусов $R$ и $r$ $(R> r)$ касаются внутренним образом в точке $A$ . Хорда $CD$ большей окружности перпендикулярна диаметру $AB$ меньшей окружности. $E$ — одна из точек пересечения $CD$ с меньшей окружностью. Найти радиус окружности, описанной около треугольника $AEC$ .

Показать ответ и решение

Обозначим центры окружностей как $O$ и $O′$ соответственно.

Тогда $′ AO = r, AO = R$ .

$PIC$

Треугольники $AEE′$ и $ACD$ равнобедренные, пусть $∠ACE = β = ∠ADE ′$ и $∠CAE = α= ∠DAE ′.$

Тогда по свойству внешнего угла треугольника $∠AED = α+ β = ∠AE′C.$

По теореме синусов в треугольнике $ACD$ получаем $AC = 2Rsinβ$

По теореме синусов в треугольнике $AEE′$ получаем

AE = AE′ = 2rsin(α +β)

Теперь применим теорему синусов к треугольнику $ACE,$ обозначив искомый радиус описанной около него окружности за $RACE :$

2RACE = --AC----= AE-- sin(α +β) sinβ

Следовательно

2 --AC---- AE-- 2R-sinβ-⋅2rsin(α+-β) 4RACE = sin(α+ β) ⋅sinβ = sin(α +β)⋅sinβ

4R2ACE = 4Rr

√ --- RACE = Rr

Ответ:

$√Rr-$

Ошибка.
Попробуйте повторить позже

Задача 9#85911

Прямая $ℓ$ касается описанной окружности треугольника $ABC$ в точке $A$ . Точки $D$ и $E$ таковы, что $CD$ и $BE$ перпендикулярны $ℓ$ , а углы $DAC$ и $EAB$ прямые. Докажите, что $BD$ и $CE$ пересекаются на высоте треугольника $ABC$ из вершины $A$ .

Источники: ФЕ - 2024, 11.3 (см. www.formulo.org)

Подсказки к задаче

Подсказка 1

Сразу обозначим точки пересечения l с CD и BE за F и G соответственно. Так как у нас фигурирует высота, то неплохой идеей было бы отметить ортоцентр H. Что про него можно сказать?

Показать доказательство

Пусть $H$ — ортоцентр $ABC.$

$AD$ перпендикулярно $AC$ и $BH$ перпендикулярно $AC$ , значит $AD∥BH$ . Пусть касательная в точке $A$ пересекает $CD$ в точке $F.$

$PIC$

$∠FAC = ∠ABC$ как угол между касательной и хордой.

∠CDA = 90∘ − ∠ACD =90∘− (90∘− ∠FAC )=∠F AC =∠ABC

Значит, точки $C,D, A,H$ лежат на одной окружности. Значит, $∠DHC$ - прямой, а значит $DH ∥AB$ .

Тогда $BADH$ — параллелограмм, а значит, $BD$ проходит через середину $AH$ . Аналогично $CE$ тоже через неё проходит, ч.т.д.

Ошибка.
Попробуйте повторить позже

Задача 10#86100

Окружности $w 1$ и $w 2$ пересекаются в точках $A$ и $B.$ Прямая $l$ расположена ближе к $A$ , чем к $B$ , и является общей касательной окружностей $w1$ и $w2$ , касаясь их соответственно в точках $T$ и $R$ . Через точку $A$ проведена параллельно касательной $l$ прямая, пересекающая $w1$ в точке $C,w2$ в точке $D$ . Прямые $TC$ и $RD$ пересекаются в точке $E,$ прямые $T B$ и $CD$ пересекаются в точке $M,$ прямые $RB$ и $CD$ пересекаются в точке $N.$ Докажите, что $TBRE$ — вписанный четырёхугольник.

Источники: Бельчонок - 2024, 11.4 (см. dovuz.sfu-kras.ru)

Подсказки к задаче

Подсказка 1

Поставим цель доказать, что противоположные углы в четырёхугольнике TBRE в сумме дают 180 градусов. Чтобы сделать это, воспользуемся свойствами вписанных четырёхугольников, которые уже есть на картинке, и отметим в них равные уголочки.

Подсказка 2

У нас есть пары углов СТВ, САВ и BAD, BRD, которые опираются на одну дугу. Воспользуется свойствами смежных углов и докажем то, что хотели! Даже свойства касательных не понадобились.

Показать доказательство

Пусть $∠BT E =α,$ а $∠BRE = β.$ Тогда смежные с ними $∠BTC = 180∘− α,∠BRD = 180∘− β.$

______________________________________________________________________________________________________________________________________________________

$PIC$

Замечание. Точки $M$ и $N$ не подписаны на чертеже, потому что в решении их использовать не будем.

_________________________________________________________________________________________________________________________________________________________________________________

В силу вписанности $ABCT$ и $ABDR$ получаем

∠BAC = ∠BTC = 180∘ − α, ∠BAD = ∠BRD = 180∘− β

Но $∠BAC$ и $∠BAD$ смежные, поэтому

(180∘ − α)+ (180∘− β)=180∘

Следовательно, $∠BTE +∠BRE =α +β = 180∘,$ так что $TBRE$ вписанный.

Ошибка.
Попробуйте повторить позже

Задача 11#87531

В круговой сектор радиуса $R$ с центральным углом $α$ $(0< α≤ π∕2)$ вписаны две окружности (обе касаются радиусов-сторон сектора, друг друга внешним образом, а большая касается окружности сектора). Какую наибольшую долю может составлять расстояние между центрами вписанных окружностей от величины $R$ и при каком значении $α$ это достигается?

Источники: Надежда энергетики - 2024, 11.4 (см. www.energy-hope.ru)

Подсказки к задаче

Подсказка 1

Попробуем ввести обозначения, переписать данное через эти переменные и выразить искомое через них. Что лучше взять за x и y?

Подсказка 2

Пусть радиусы окружностей будут x и y. Мы можем записать следствие из подобия прямоугольных треугольников с катетами - радиусами окружностей. Как можно выразить (x + y) / R?

Подсказка 3

Пусть t = y / R. Тогда искомое можно выразить через t. Это будет парабола, наибольшее значение которой на отрезке можно найти через вершину.

Показать ответ и решение

Обозначим радиусы малой и большой вписанных окружностей через $x$ и $y$ , введём величину $β = α 2$ . Отметим, что $π 0 <β < 4$ .

$PIC$

Выразим стороны треугольника через радиусы трёх окружностей.

OO2 = R − y, OO1 = R− x− 2y

Из подобия прямоугольных треугольников получаем

--1-= R-− y-= R−-x−-2y sin β y x

Откуда

R-= R-− 2x y x

-x y- y- R = (1− 2⋅R)⋅R

Расстояние между центрами вписанных окружностей $O1O2$ равно $x+y$ .

Рассмотрим искомое отношение

x +y y y y y y --R- = (1− 2R)R-+ R-= 2(1− R)R-

Относительно величины $t= yR-$ это отношение есть парабола $2t(t− 1)$ . Выразим параметр $t$ через угол $β$ .

si1nβ = Ry − 1

t= y= --sinβ--= ---1--- R 1 +sinβ 1+ s1inβ

Таким образом, при изменении $β$ от $0$ до $π 4$ параметр $t$ растёт от $0$ до $√ - 2− 1$ . Остаётся найти максимум параболы $2t(1− t)$ на полученном отрезке $√- [0; 2− 1]$ . Вершина параболы лежит правее отрезка, следовательно искомый максимум достигается при $√- t= t0 = 2− 1$ и равен $√ - 2(3 2− 4)$ .

Ответ:

$2(3√2-− 4)$ при $α= π 2$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#67592

Диагонали вписанного четырехугольника $ABCD$ пересекаются в точке $K$ . Докажите, что касательная в точке $K$ к окружности, описанной около треугольника $ABK$ , параллельна $CD.$

Подсказки к задаче

Подсказка 1

Самый лучший способ решения задач по планиметрии следующий. Пусть вопрос задачи верен, какие тогда факты оттуда можно было бы подметить? Тем самым то есть мы раскручиваем задачу с конца и понимаем, что от нас требуется доказать, например, равенство каких уголочков и т.п. Давайте поступим здесь так же. Пусть прямые параллельны. Какие тогда равные углы вы можете отметить?

Показать доказательство

$PIC$

Отметим на касательной точку $M.$ Угол между касательной $MK$ и хордой $BK$ равен вписанному углу $BAK.$ Кроме того, $∠BAC =∠CDB$ как вписанные, опирающиеся на одну дугу. Таким образом, $∠MKB = ∠CDB,$ следовательно, $MK ||CD.$

Ошибка.
Попробуйте повторить позже

Задача 13#67593

В треугольнике $ABC$ проведены высоты $AA 1$ , $BB 1$ и $CC 1$ . Точка $M$ — середина $BC$ . Докажите, что:

(a) касательная в точке $A$ к описанной окружности треугольника $ABC$ параллельна прямой $B1C1$ ;

(b) прямые $MB1$ и $MC1$ касаются описанной окружности треугольника $AB1C1.$

Подсказки к задаче

Подсказка 1

У нас на картинке есть касательная к описанной окружности. Какой теоремой, связывающей уголочки, мы можем воспользоваться?

Подсказка 2

Конечно теоремой о угле между касательной и хордой! А именно: угол между касательной и хордой AB равен углу ACB. А что мы можем сказать про четырехугольник BCB₁C₁?

Подсказка 3

На самом деле он вписан, ведь углы BC₁C и BB₁C равны 90° и смотрят на отрезок BC. Осталось воспользоваться фактом, что во вписанном четырехугольнике сумма противоположных углов равна 180° и дело в шляпе!

Подсказка 4

Давайте докажем, что уголочки BB₁M и B₁AA₁ равны, тогда из обратной теоремы об угле между касательной и хордой мы получим, что MB₁ касается описанной окружности треугольника AB₁C₁.

Подсказка 5

Начнем с уголочка B₁AA₁. Что мы можем сказать о четырехугольнике AB₁A₁B?

Подсказка 6

Он вписан, т.к. уголки AB₁B и AA₁B равны 90°. Тогда B₁AA₁ равен углу B₁BA₁, т.к. они опираются на дугу B₁A₁. Теперь осталось доказать, что B₁BA₁, который равен B₁BM, равен BB₁M...

Подсказка 7

Если это так, то треугольник BMB₁ должен быть равнобедренный. А это действительно так, ведь медиана В₁M, проведенная из вершины прямого угла, равна половине основания ВС, а значит B₁M=BM. Теперь осталось провести аналогичные рассуждения для углов C₁AA₁ и МС₁С и завершить решение задачи.

Показать доказательство

(a) Отметим на касательной точку $D.∠DAB =∠ACB$ по свойству угла между хордой и касательной. В свою очередь $∠ACB =∠AC1B1$ в силу вписанности четырехугольника $BC1B1C.$ $∠DAB = ∠AC1B1,$ следовательно $DA ||C1B1.$

$PIC$

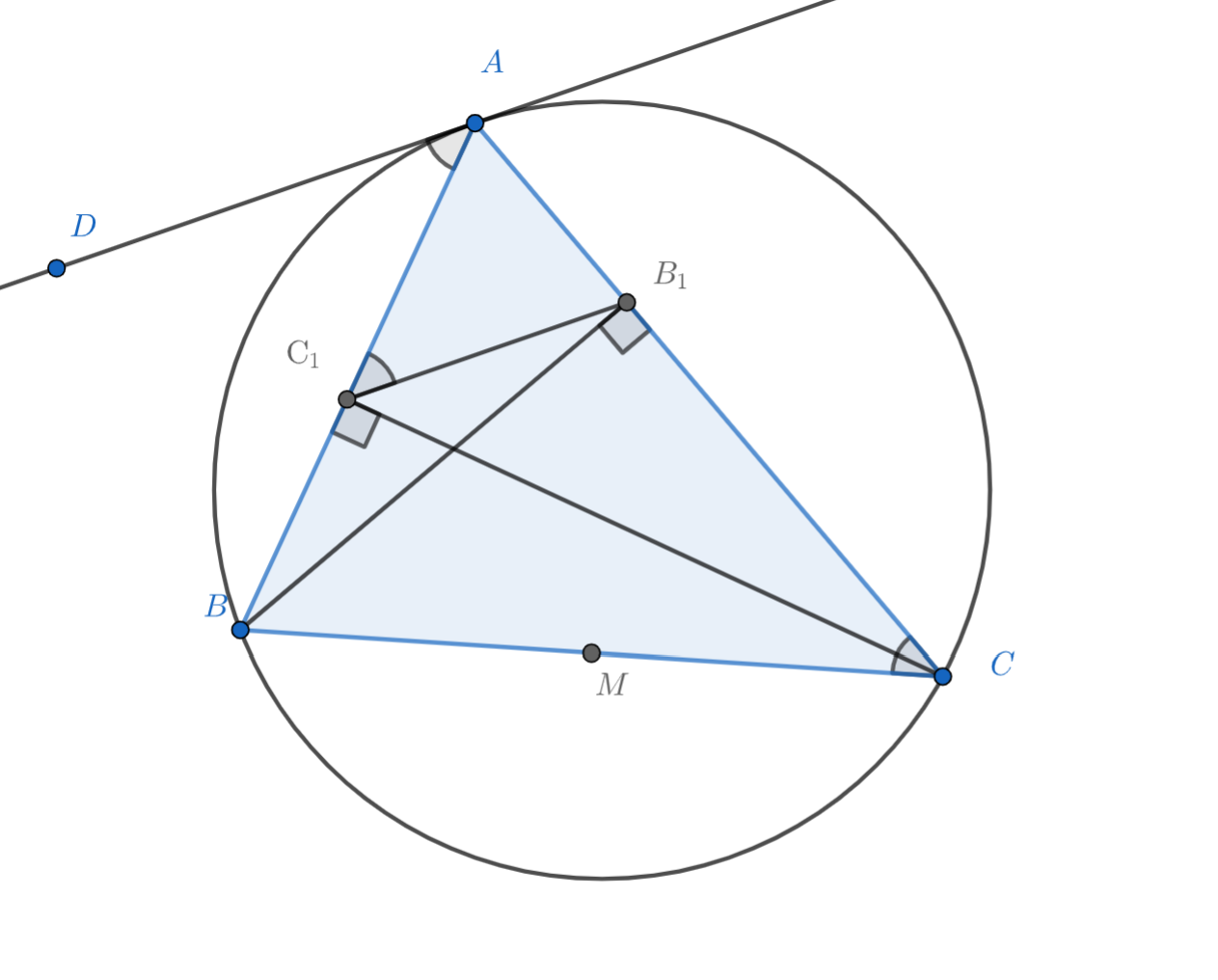
(b) Чтобы доказать, что прямые $MB1$ и $MC1$ касаются описанной окружности треугольника $AB1C1,$ докажем, что $∠BB1M = ∠B1AA1$ и $∠CC1M = ∠A1AB$ — углы между $MB1, MC1$ и хордами $B1H, C1H.$ соответственно.

$PIC$

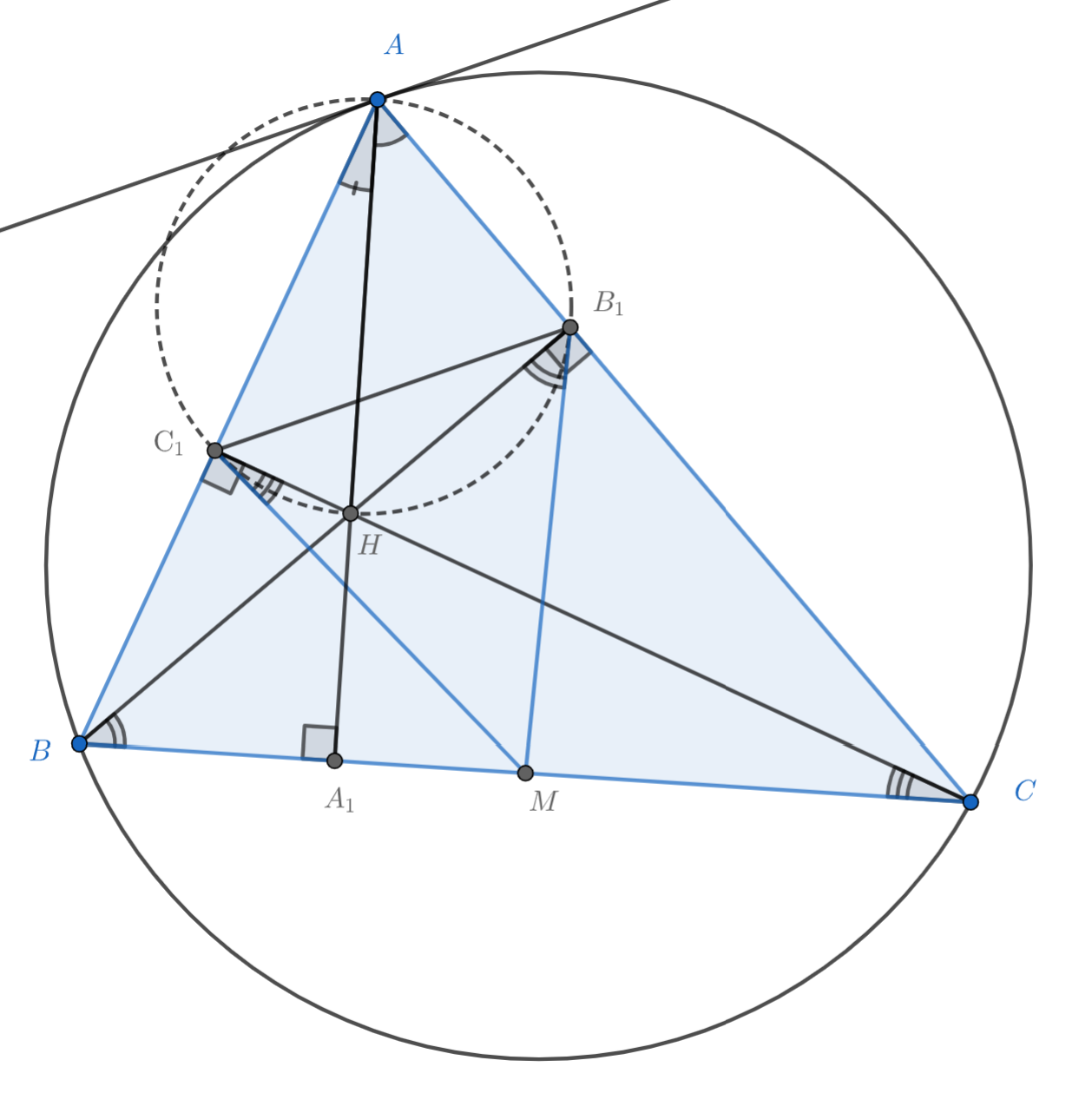
Так как $AB1HC1$ — вписанный, точка $H$ лежит на окружности, описанной около треугольника $AB1C1.$

Так как $M$ — середина $BC$ , то $MC = MB1 =MC1 =MB$ по свойству медианы прямоугольных треугольников $BB1C$ и $BC1C.$

Пусть $∠MB1B = α.$ Тогда $∠B1BM = α$ и следовательно $∠BHA1 =90∘− α= ∠AHB1$ и тогда $∠HAB1 =α.$ Итого $MB1$ — касательная к окружности, описанной около треугольника $AB1C1.$ Аналогично доказывается для $MC1.$

Ошибка.
Попробуйте повторить позже

Задача 14#67594

Две прямые, касающиеся данной окружности в точках $A$ и $B$ , пересекаются в точке $C$ . Докажите, что центр окружности, вписанной в треугольник $ABC$ , лежит на данной окружности.

Подсказки к задаче

Подсказка 1

Подумаем, а как же нам подобраться к центру вписанной окружности...чем же он является для треугольника ABC?

Подсказка 2

Точкой пересечения биссектрис! А как же нам ее найти? I лежит на какой-то биссектрисе треугольника АВС. Значит было бы хорошо провести какую-то биссектрису. О какой биссектрисе мы знаем достаточно для того, чтобы ее провести?

Подсказка 3

СО, где О - центр окружности из условия, является биссектрисой угла АСВ. А, значит, если мы проведем СО, то хочется, чтобы этот отрезок пересекал окружность именно в I. Значит, попробуем доказать, что AI, BI - биссектрисы. Чем из условия мы практически не пользовались?

Подсказка 4

Тем, что АC, BC - касательные! А это значит, что можно посчитать углы между касательной и хордой!

Показать доказательство

$PIC$

Пусть $O$ — центр данной окружности. Обозначим через через $I$ точку пересечения $OC$ с окружностью. Достаточно проверить, что $I$ — точка пересечения биссектрис углов $A$ и $B$ треугольника $ABC.$

$∠CAI = ⌣A2I$ как угол между хордой $AI$ и касательной $AC.$

$∠BAI = ⌣B2I.$ B свою очередь $⌣B2I= ⌣A2I$ в силу симметрии относительно $OC.$ Следовательно, $AI$ — биссектриса. Аналогично $BI$ — биссектриса.

Ошибка.
Попробуйте повторить позже

Задача 15#67826

В вершине $B$ остроугольного треугольника $ABC$ восставили перпендикуляры к сторонам $AB$ и $BC$ до пересечения с прямой $AC$ в точках $P$ и $Q$ . Докажите, что описанные окружности треугольников $ABC$ и $PBQ$ касаются.

Показать доказательство

Первое решение.

$PIC$ Достаточно показать, что для этих двух окружностей касательная в точке $B$ общая. Тогда проведем касательную в этой же точке к окружности, описанной около $ABC,$ пусть она пересекает продолжение стороны $AC$ в точке $X.$ Из свойства касательной имеем:

∘ ∘ ∠PBX = 180 − (∠ABP + ∠ACB )=90 − ∠ACB.

Из прямоугольного треугольника $CBQ$ по теореме о сумме углов треугольника получим, что $∠CQB = 90∘ − ∠ACB.$ Тем самым мы доказали верность равенства $∠P BX = ∠CQB,$ а это означает, что проведенная касательная также является касательной к описанной около треугольника $PBQ$ окружности.

Второе решение.

Пусть $O$ и $O1$ — центры окружностей, описанных около треугольников $ABC$ и $PBQ$ соответственно. Проведем $BK$ — высоту из точки $B$ в треугольниках $ABC$ и $PBQ$ .

$PIC$

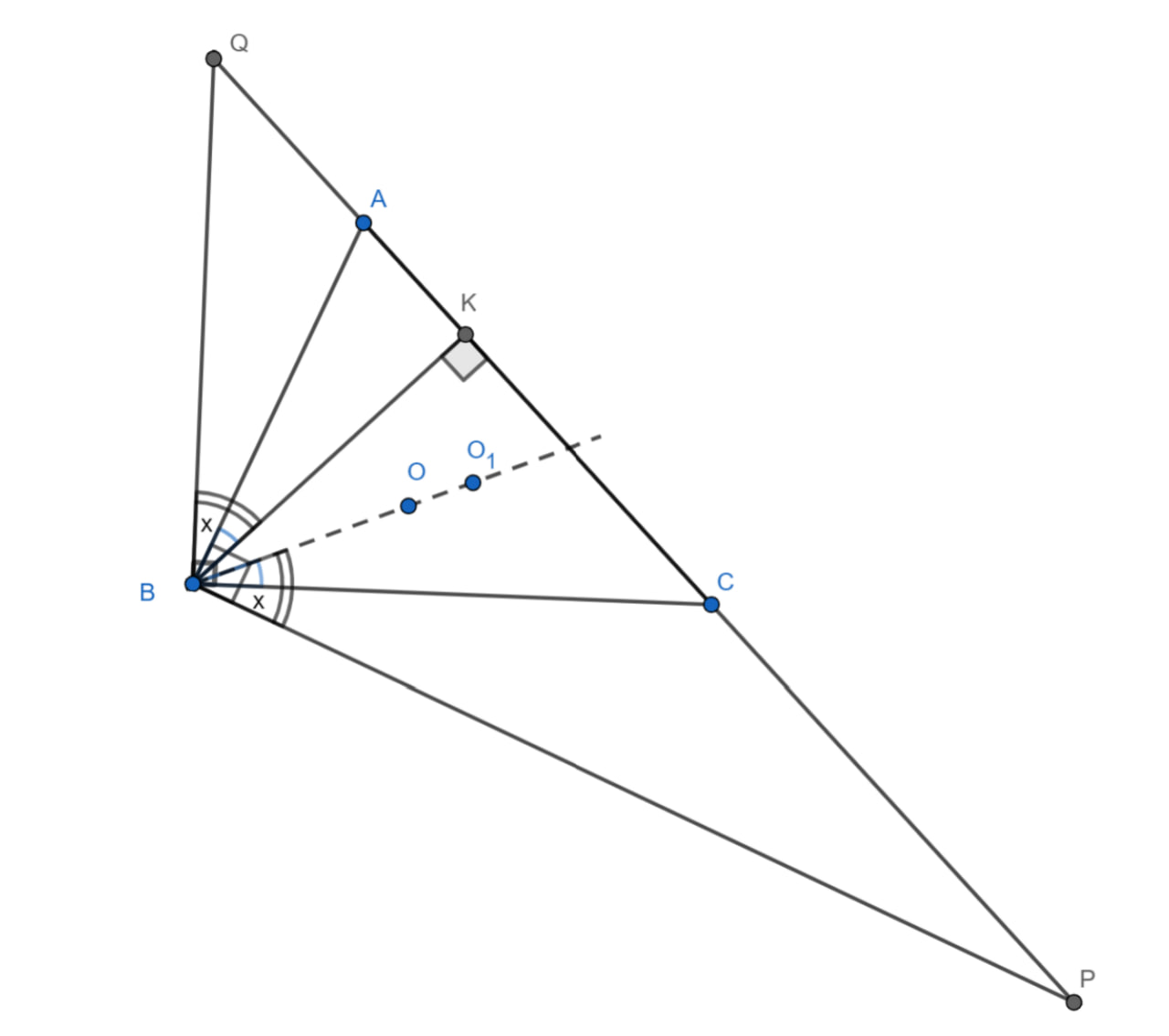
Вспомним одно из свойств ортоцентра: $∠ABK =∠CBO,$ где $O$ — центр описанной около треугольника $ABK$ окружности.

$PIC$

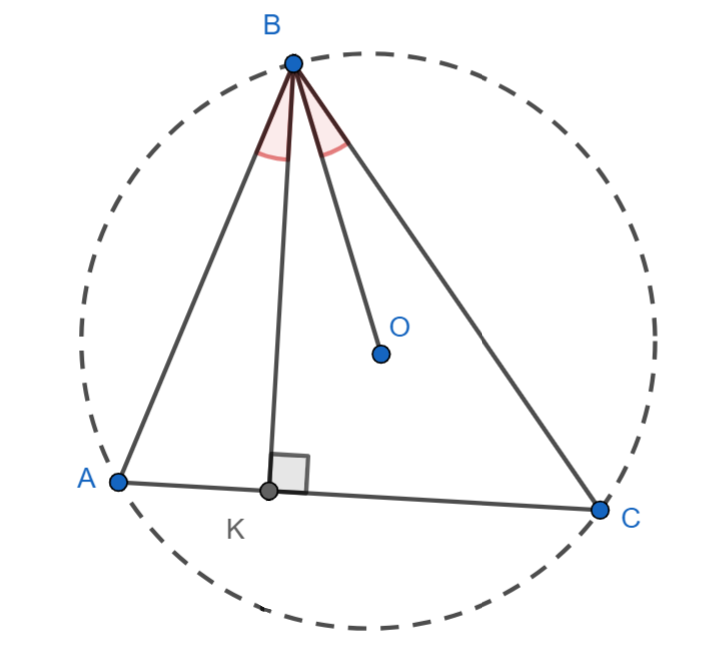
Докажем, что $O$ и $O1$ лежат с точкой $B$ на одной прямой, тем самым докажем, что окружности касаются внутренним образом в точке $B$ .

$∠QBA = ∠CBP = x,$ а $∠ABK = ∠OBC$ по свойству ортоцентра для треугольника $ABC$ . Следовательно, $∠QBK = ∠OBP,$ значит $O1$ лежит на одной прямой с $O$ , так как $∠QBK =∠O1BP$ по свойству ортоцентра для треугольника $BPQ$ .

Ошибка.
Попробуйте повторить позже

Задача 16#69400

Дан прямоугольный треугольник $KLM$ с прямым углом $M.$ На его катете $LM$ длины 52 как на диаметре построена окружность $ω.$ Из точки $K$ к этой окружности проведена касательная $KD,$ отличная от $KM.$ Перпендикуляр $DH,$ опущенный на отрезок $LM,$ пересекает отрезок $KL$ в точке $E.$ Найдите площадь треугольника $LDE,$ если известно, что $LH :MH =4 :9.$

Источники: Бельчонок-2023, 11.2 (см. dovuz.sfu-kras.ru)

Подсказки к задаче

Подсказка 1

Для начала попробуем найти всё, что можем)) Воспользуемся всеми условиями на LH, LM, MH и найдем их) Тогда будет несложно найти оставшиеся отрезки на LM и DH! На картинке много прямых углов...что хочется сделать?

Подсказка 2

Найти среди них подобные! Учтём, что угол между касательной и радиусом прямой, тогда какие треугольники будут подобными (или даже равными)?

Подсказка 3

Треугольники MKO и KOD будут равными, тогда треугольники LHD и OKM будут подобны! Найдём отношение KM/LM. Теперь нам необходимо найти площадь треугольника LED, как можно это сделать?

Подсказка 4

Найдя его высоту и стороны! Высота его это LH, а в каких подобных треугольниках этот отрезок встречается, чтобы его найти?

Подсказка 5

Треугольники LHE и LMK подобны, поэтому несложно найти EH! Осталось лишь найти DE через DH и EH, что сделать из подобия несложно)

Показать ответ и решение

$PIC$

Пусть $O$ — центр окружности $ω.$ Заметим, что

∘ --------- LH =-4LM =16, MH = 36, OH = 1LM − LH = 10, DH = OD2 − OH2 = 24 13 2

Прямоугольные треугольники $LHD$ и $OMK$ подобны, поскольку

∠MLD = 1∠MOD = 1(180∘ − ∠MKD )= 90∘ − ∠MKO = ∠MOK 2 2

Тогда

KM-- 1 KM-- 1 DH- 3 LM = 2 ⋅OM = 2 ⋅LH = 4

Из подобия треугольников $LHE$ и $LMK$ мы получаем

3 EH = 4LH = 12

Поэтому

1 1 1 SLDE = 2 ⋅DE ⋅LH = 2 ⋅(DH − EH )⋅LH = 2 ⋅12⋅16 =96

Ответ: 96

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#70337

Касательная в точке $A$ к описанной окружности треугольника $ABC$ пересекает прямую $BC$ в точке $E$ ; $AM$ — биссектриса треугольника $ABC$ . Докажите, что $AE = EM$ .

Подсказки к задаче

Подсказка 1

Попробуем записать условие на языке углов. Обозначим, что AM это биссектриса, и AE это касательная в точке A. Что это означает?

Показать доказательство

$PIC$

Пусть $∠BAM = ∠MAC = α, ∠EAB = β.$ Тогда по свойству угла между хордой и касательной $∠ACM = ∠EAB = β.$ В треугольнике $EAM ∠EAM =α +β = ∠EMA$ так как $∠EMA$ — внешний угол треугольника $AMC.$ Следовательно, треугольник $EAM$ — равнобедренный и $AE = EM.$

Ошибка.
Попробуйте повторить позже

Задача 18#70338

Две окружности касаются в точке $A$ . К ним проведена общая внешняя касательная, касающаяся окружностей в точках $C$ и $B$ . Найдите $∠CAB$ .

Показать ответ и решение

$PIC$

$MB =MA$ как отрезки касательных из точки $M$ к первой окружности, $MA = MC$ как отрезки касательных из $M$ ко второй окружности. Тогда в треугольнике $ABC$ медиана $AM$ равна половине стороны, к которой она проведена. Следовательно, треугольник $ABC$ — прямоугольный и $∠CAB = 90∘.$

Ответ:

$90∘$

Ошибка.
Попробуйте повторить позже

Задача 19#70339

Две окружности пересекаются в точках $P$ и $Q$ . Через точку $A$ первой окружности проведены прямые $AP$ и $AQ$ , пересекающие вторую окружность в точках $B$ и $C$ . Докажите, что касательная в точке $A$ к первой окружности параллельна прямой $BC$ .

Показать доказательство

$PIC$

Угол между касательной в точке $A$ и хордой $AP$ равен углу $AQP.$ Из вписанности $PBCQ$ следует равенство углов $PBC$ и $AQP.$ Итого накрест лежащие углы равны, следовательно, касательная в точке $A$ и прямая $BC$ параллельны.

Замечание. Картинка может быть другой, но рассуждения такие же

$PIC$

Ошибка.
Попробуйте повторить позже

Задача 20#70341

Высоты $AA 1$ и $BB 1$ остроугольного треугольника $ABC$ пересекаются в точке $H.$ Прямая $CH$ пересекает полуокружность с диаметром $AB,$ проходящую через точки $A1$ и $B1,$ в точке $D.$ Отрезки $AD$ и $BB1$ пересекаются в точке $M,BD$ и $AA1$ — в точке $N.$ Докажите, что описанные окружности треугольников $B1DM$ и $A1DN$ касаются.

Показать доказательство

Отметим $O$ — середину $AB,$ то есть центр полуокружности. Докажем, что $DO$ — общая касательная для окружностей, описанных около треугольников $B1DM$ и $A1DN.$

Для этого, в силу теоремы об угле между хордой и касательной, покажем, что $∠DA1N =∠NDO$ и $∠DB1M = ∠MDO.$

$PIC$

В силу вписанности четырехугольника $DA1BA ∠DA1A =∠DBA$ как вписанные, опирающиеся на одну дугу. Далее $OD =OB$ как радиусы, следовательно $∠DBA = BDO.$ Итого $∠DA1N = ∠NDO.$ Аналогично доказывается $∠DB1M =∠MDO.$

Предыдущий раздел

Следующий раздел